算額(その51)改訂版
色々思いがけないこともあったので,改訂版を書いた。初版
岩手県一関市萩荘 達古袋八幡神社 弘化3年(1846)8月
参考文献
(1). 和算の館 岩手県 達古袋八幡神社2
http://www.wasan.jp/iwate/tatukohatiman2.html
(2). 二十三 岩手県一関市萩荘 達古袋八幡神社 弘化3年(1846)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
(3). 今有如図 03029
https://w.atwiki.jp/sangaku/pages/288.html
(4). 今有如図 03021
https://w.atwiki.jp/sangaku/pages/209.html
(5). 八十九 岩手県陸前高田市小友町 常膳寺観音堂 天保13年(1842)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
問: (2) 今有大円内如図設中円容小円及甲乙円各三ケ其中円径若干問得大円径術如何
(3) 今有大円内如図設中円容小圓及甲乙円各三个其中円径若干問得大円径術如何
術: (2) 術曰置四十八個開平方加二十三個乗中円径九除之得大円径合問
(3) 術曰置四十八個開平方加二十三個乗中円径九除之得大円径合問
問を意訳すると,「大円の中に 中円を 1 個,甲円,乙円,小円を 3 個ずつ容れる。中円の直径が与えられたとき,大円の直径を求める術を述べよ」。
術は,「48 の平方根に 23 を加え,中円の直径を掛けて,9 で割れば大円の直径が得られる」。
山村の図,解釈は不適切である。
真ん中にあるのが中円で,「中円」と描かれているのは甲円である。このような誤解が生まれたのは,元の算額の図が不鮮明であることが原因であろうが,問に「小円及甲乙円各三個」と書かれているのに,図に「小円」を 4 個描いたという矛盾に気づかなかったのか?
筆者自身は,自分の書いた記事「算額(その51)」が同じ対象であることに気づかなかった。図があまりにも違ったためでもある。
筆者はかつて (1) の写真にのみ基づいて,「算額(その51)」を書いた。写真は露出・コントラストなどを補正した。
当時はインターネットでの検索にまで気が回らず,問は読み取れず,どの円がどれかもわからない不明瞭な図のみから円の位置関係について仮説を立て,解を導いた。
後に,その仮定は (3) と同じであることを知った。
今,3つの参考文献に基づいて,「算額(その51)」の改訂版を書き,その途上で色々な情報を得た。
結論は,「術の記述の際に 448 を 48 と書き誤ったのであろう」である。
---

大円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r4, (x4, y4)
乙円の半径と中心座標を r3, (0, R - r3)
小円の半径と中心座標を r1, (0, r1 + r2)
中円の半径と中心座標を r2, (0, 0)
とおき,中円の直径を既知として,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, r2::positive, r3::positive,
r4::positive, x4::positive, y4::positive;
x4 = (R - r4)cos(PI/6)
y4 = (R - r4)sin(PI/6)
eq1 = x4^2 + (y4 - r2 - r1)^2 - (r1 + r4)^2 |> expand
eq2 = x4^2 + y4^2 - (r2 + r4)^2 |> expand
eq3 = x4^2 + (R - r3 - y4)^2 - (r3 + r4)^2 |> expand
eq4 = r2 + 2r1 + 2r3 - R
res = solve([eq1, eq2, eq3, eq4], (R, r1, r3, r4))[1]
(r2*(8*sqrt(7) + 23)/9, r2*(1 + sqrt(7))/6, r2*(11 + 5*sqrt(7))/18, r2*(7/9 + 4*sqrt(7)/9))
大円の半径 R は,中円の半径 r2 の (8*√7 + 23)/9 = (√448 + 23)/9 倍である。
中円の直径が 1 寸のとき,大円の直径は (√448 + 23)/9 = 4.90733449872408 である。
術は「48 の平方根に 23 を加え,中円の直径を掛けて,9 で割れ」である。参考文献の (2) も (3)も「置四十八個」としている。確かに (1) の写真も露出・コントラストを調整すると「置四十八個」と読み取れる。448 を 48 と書き損じたか。
今まで,誰も実際に算額を解いた人はいないので,見逃されてきたのか。
ここで,(3) の備考欄に「類題 3021」とあり,その「類題 3021」は岩手県陸前高田市小友町の常膳寺である(4)ことがわかった。
岩手県陸前高田市小友町の常膳寺の算額も「現存 岩手の算額」に掲載されている(5)。この図も不適切ではある。
そこには,筆者のメモ書きで「算額(その51)に似ている?」と書かれている。実際には解いていない。山村も両者が同じものであるという認識はなかったようだ。なにせ,同じとは思えない図を描いているのだから。
その術文にはしっかりと「置四百四十八個」と書いてある。「答」も「全円径四寸九分有奇」となり,筆者の得た解 4.90733449872408 と一致する。
達古袋八幡神社の算額は弘化3年(1846)黄川田桃蔵忠一で,上善寺観音堂の算額は天保13年(1842)佐藤長太郎誠定の 4 年後の奉納である。
結論:本問は上善寺観音堂の算題を解いた黄川田が奉納するとき,書き誤った(脱字)ものと思う。
算額は,先人の問題を後輩が解くということも多かったようだが,引用元を記載するという習慣はなかったようだ。
function draw(r2, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r1, r3, r4) = (r2*(8*sqrt(7) + 23)/9, r2*(1 + sqrt(7))/6, r2*(11 + 5*sqrt(7))/18, r2*(7/9 + 4*sqrt(7)/9))
x4 = (R - r4)cos(π/6)
y4 = (R - r4)sin(π/6)
@printf("中円の直径が %g のとき,大円の直径は %g である。\n", 2r2, 2R)
@printf("r2 = %g; R = %g; r1 = %g; r3 = %g; r4 = %g; x4 = %g; y4 = %g\n", r2, R, r1, r3, r4, x4, y4)
plot()
circle(0, 0, R, :black)
circle(0, 0, r2, :magenta)
rotate(0, r2 + r1, r1)
rotate(0, R - r3, r3, :blue)
rotate(x4, y4, r4, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, R, "大円:R", :black, :center, :bottom, delta=delta/2)
point(0, r2, "r2", :magenta, :center, delta=-delta/2)
point(0, 0, "中円:r2(0,0)", :magenta, :center, delta=-delta/2)
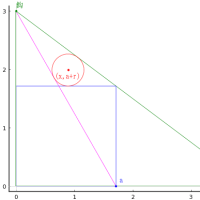
point(0, r1 + r2, "小円:r1,(0,r1+r2)", :red, :right, :vcenter, deltax=-5delta)
point(0, R - r3, "乙円:r3,(0,R-r3)", :blue, :center, delta=-delta/2)
point(x4, y4, "甲円:r4,(x4,y4)", :green, :center, delta=-delta/2)
end
end;
draw(1/2, true)



























※コメント投稿者のブログIDはブログ作成者のみに通知されます