算額(その854)
廃版 図が正しくないため
算額(その866)を参照のこと
十八 岩手県平泉町 弁慶堂(現在は地蔵堂にて保管) 安政6年(1859)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市. http://www.wasan.jp/yamamura/yamamura.html
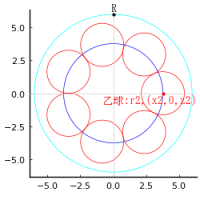
正方形内に斜線を 2 本引き(右下頂点を通る甲斜,左下と右上の頂点を通る対角線の乙斜),正方形に内接する円(予円と書かれている)と乙円,丙円,丁円,戊円の 4 円を入れる。正方形の一辺の長さが与えられたとき,「甲斜,乙・丙・丁・戊・己円の直径の六和」を求めよ。

まず,「己円」が定義されていないという大問題がある。4 円の名前が乙円から始まっているのも不自然であるが,正方形に内接する円は「予円」と名付けられている。予と己を誤記するとも思えない。(山村の誤記か,もともとの誤記かもわからないが)
問は(術に示すように),「甲斜の引き方によらず,六和は正方形の一辺の長さに定数を掛けたものになる」ことを意図しているのであろうが,とりあえずは正方形の一辺の長さと甲斜の位置を与えて結果がどうなるかを見てみよう。
問を解く前に述べておくが,術は,「二個開平方以滅二個開平方加三個乗方面」とあり,山村は,
六和 = (sqrt(2 - √2) + 3)×方 = 4.8477×方
としているが,そもそも (sqrt(2 - √2) + 3) = 3.7653668647301792 である(これは山村の誤記であろう)。
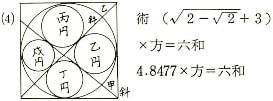
以上の諸問題があるが,六和を求める以前に,図形を描くことができるかどうかを検討する。

正方形の一辺の長さを a, 甲斜と正方形の一辺との交点座標を (0, b)
乙円,丙円,丁円,戊円の半径と中心座標を,r2,(x2, y2) ... r5,(x5,y5)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
dist2(x1, y1, x2, y2, x3, y3, r) = numerator(apart(dist(x1, y1, x2, y2, x3, y3) - r^2, d))
@syms d, a, b, r2, x2, y2, r3, x3, y3, r4, x4, y4, r5, x5, y5
# (X0, Y0) = intersection(0, 0, a, a, a, 0, 0, b)
# (X1, Y1) = intersection(x2, y2, x5, y5, x3, y3, x4, y4)
eq1 = (x2 - a/2)^2 + (y2 - a/2)^2 - (a/2 - r2)^2 |> expand
eq2 = (x3 - a/2)^2 + (y3 - a/2)^2 - (a/2 - r3)^2 |> expand
eq3 = (x4 - a/2)^2 + (y4 - a/2)^2 - (a/2 - r4)^2 |> expand
eq4 = (x5 - a/2)^2 + (y5 - a/2)^2 - (a/2 - r5)^2 |> expand
eq5 = dist2(0, 0, a, a, x2, y2, r2)
eq6 = dist2(0, 0, a, a, x3, y3, r3)
eq7 = dist2(0, 0, a, a, x4, y4, r4)
eq8 = dist2(0, 0, a, a, x5, y5, r5)
eq9 = dist2(a, 0, 0, b, x2, y2, r2)
eq10 = dist2(a, 0, 0, b, x3, y3, r3)
eq11 = dist2(a, 0, 0, b, x4, y4, r4)
eq12 = dist2(a, 0, 0, b, x5, y5, r5)
# eq13 = X1 - X0 |> simplify |> numerator
# eq14 = Y1 - Y0 |> simplify |> numerator
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return Float64.(v), r.f_converged
end;
function H(u)
(r2, x2, y2, r3, x3, y3, r4, x4, y4, r5, x5, y5) = u
return [
a^2/4 + a*r2 - a*x2 - a*y2 - r2^2 + x2^2 + y2^2, # eq1
a^2/4 + a*r3 - a*x3 - a*y3 - r3^2 + x3^2 + y3^2, # eq2
a^2/4 + a*r4 - a*x4 - a*y4 - r4^2 + x4^2 + y4^2, # eq3
a^2/4 + a*r5 - a*x5 - a*y5 - r5^2 + x5^2 + y5^2, # eq4
-r2^2 + x2^2/2 - x2*y2 + y2^2/2, # eq5
-r3^2 + x3^2/2 - x3*y3 + y3^2/2, # eq6
-r4^2 + x4^2/2 - x4*y4 + y4^2/2, # eq7
-r5^2 + x5^2/2 - x5*y5 + y5^2/2, # eq8
a^2*b^2 - 2*a^2*b*y2 - a^2*r2^2 + a^2*y2^2 - 2*a*b^2*x2 + 2*a*b*x2*y2 - b^2*r2^2 + b^2*x2^2, # eq9
a^2*b^2 - 2*a^2*b*y3 - a^2*r3^2 + a^2*y3^2 - 2*a*b^2*x3 + 2*a*b*x3*y3 - b^2*r3^2 + b^2*x3^2, # eq10
a^2*b^2 - 2*a^2*b*y4 - a^2*r4^2 + a^2*y4^2 - 2*a*b^2*x4 + 2*a*b*x4*y4 - b^2*r4^2 + b^2*x4^2, # eq11
a^2*b^2 - 2*a^2*b*y5 - a^2*r5^2 + a^2*y5^2 - 2*a*b^2*x5 + 2*a*b*x5*y5 - b^2*r5^2 + b^2*x5^2, # eq12
]
end;
a = 100
b = 50
iniv = BigFloat[24.8, 82, 47, 26.7, 39, 77, 18.2, 45, 19, 15.7, 18, 40]
res = nls(H, ini=iniv)
println(res)
([24.042227875260373, 73.9205817737793, 39.91973704292161, 24.664395829520114, 28.463273173025932, 63.34399626287168, 13.777280329715465, 36.05369934249495, 16.569682647595275, 10.478025010198175, 15.644697884880152, 30.4628629611869], true)
「己円」が「予円」であるとしても,b を変えれば「六和」も変わる。
したがって,この問題は「無術」と思われる。
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
a = 100
b = 50
(r2, x2, y2, r3, x3, y3, r4, x4, y4, r5, x5, y5) = res[1]
plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
circle(a/2, a/2, a/2, :brown)
circle(x2, y2, r2)
circle(x3, y3, r3, :green)
circle(x4, y4, r4, :magenta)
circle(x5, y5, r5, :orange)
segment(0, 0, a, a, :green)
segment(0, b, a, 0, :green)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x2, y2, "乙円:r2,(x2,y2)", :red, :center, delta=-delta/2)
point(x3, y3, "丙円:r3,(x3,y3)", :magenta, :center, delta=-delta/2)
point(x4, y4, "丁円:r4,(x4,y4)", :orange, :center, delta=-delta/2)
point(x5, y5, "戊円:r5\n(x5,y5)", :green, :center, delta=-delta/2)
point(a/2, a/2, " 予円", :brown, :left, :vcenter)
point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
point(0, a, " a", :blue, :left, :bottom, delta=delta/2)
end
end;