算額（その1391）

算額（その1391）

十八 大里郡岡部村岡 稲荷社
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円5個，斜線2本
#Julia, #SymPy, #算額, #和算

5 個の円が，2 本の直線に挟まれている。大円の直径が 2 寸のとき，中円の直径はいかほどか。

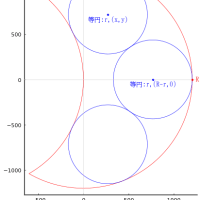
元の図を反時計回りに 90 °回転させたもので考える。
小円の位置が元図と違うが，大円と中円の中心を結ぶ直線に関して対称なのでこの図のままでよい。

大円の半径と中心座標を r1, (x1, r1)
中円の半径と中心座標を r2, (0, r2)
小円の半径を r3, 右側の小円の中心座標を (x3, r3)，左側の小円の中心座標を (-x3 - 2r3, r3)
とおき，以下の連立方程式を解く。

eq1, eq2, eq3 は，大円，中円，右側の小円が互いに接しているという中心間の水平距離に関する条件式である。
eq4 は，大円と中円の水平距離と中円と左側の小円の水平距離（灰色で描いた相似の直角三角形の底辺と高さ）に関する条件式である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r1::positive, x1::positive,
     r2::positive, r3::positive,
     x3::positive

eq1 = x1 - 2sqrt(r1*r2)
eq2 = (x1 - x3) - 2sqrt(r1*r3)
eq3 = x3 - 2sqrt(r2*r3)
eq4 = (r1 - r2)/x1 - (r2 - r3)/(x3 + 2r3);

一度に解けないので，まず eq1, eq2, eq3 を解いて x1, r3, x3 を求める。

res = solve([eq1, eq2, eq3], (x1, r3, x3))[1]

   (2*sqrt(r1)*sqrt(r2), r1*r2/(sqrt(r1) + sqrt(r2))^2, 2*sqrt(r1)*r2/(sqrt(r1) + sqrt(r2)))

eq4 に x1, r3, x3 を代入し（eq14 とする），r2 について解く。

eq14 = eq4(x1 => res[1], r3 => res[2], x3 => res[3])
ans_r2 = solve(eq14, r2)[1]
ans_r2 |> println

   r1/2

中円の半径 r2 は，大円の半径の 1/2 である。
大円の直径が 2 寸のとき，中円の直径は 1 寸である。

いきなり solve() でよいが， どういうふうに解かれているかは，以下のようなものでもあろう。
まず，x1, r2, x3 を代入した方程式を簡約化し，分数式になったので，その分子を取り出して，分子 = 0 を解く。

eq14 = eq4(x1 => res[1], r3 => res[2], x3 => res[3]) |> simplify |> numerator
eq14 |> println

   r1^(3/2)*r2^(3/2)/2 - sqrt(r1)*r2^(5/2) + r1^2*r2 - 2*r1*r2^2

式が因数分解できれば，解がすぐわかる。ルートを含むそのままの式は SymPy では因数分解できないので，変数を置き換えて因数分解した後元の変数に戻す。

@syms s, t
eq14(√r1 => s, √r2 => t) |> factor |> x -> x(s => √r1, t => √r2) |> println

   sqrt(r1)*r2*(2*sqrt(r1) + sqrt(r2))*(r1 - 2*r2)/2

方程式の解は，r1 - 2*r2 = 0，つまり，r2 = r1/2 である。

全てのパラメータは以下のとおりである。

  r1 = 1;  r2 = 1.41421;  x1 = 0.5;  r3 = 0.171573;  x3 = 0.585786

function draw(r1, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = r1/2
   (x1, r3, x3) = (2*sqrt(r1)*sqrt(r2), r1*r2/(sqrt(r1) + sqrt(r2))^2, 2*sqrt(r1)*r2/(sqrt(r1) + sqrt(r2)))
   @printf("大円の直径が %g のとき，中円の直径は %g である。\n", 2r1, 2r2)
   @printf("r1 = %g;  x1 = %g;  r2 = %g;  r3 = %g;  x3 = %g\n", r1, x1, r2, r3, x3)
   plot()
   circle
   circle(x1, r1, r1)
   circle(0, r2, r2, :green)
   circle2(x3, r3, r3, :blue)
   circle(-x3 - 2r3, r3, r3, :blue)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       plot!([-x3 - 2r3, 0, 0, -x3 - 2r3], [r3, r3, r2, r3], color=:gray60, lw=0.5)
       plot!([0, x1, x1, 0], [r2, r2, r1, r2], color=:gray60, lw=0.5)
       point(x1, r1, "大円:r1,(x1,r1)", :red, :center, :bottom, delta=delta)
       point(0, r2, "中円:r2,(0,r2)", :green, :center, :bottom, delta=4delta)
       point(x3, r3, "小円:r3,(x3,r3)", :blue, :center, delta=-7delta)
       point(-x3 - 2r3, r3, "小円:r3,(-x3-2r3,r3)", :blue, :center, delta=-7delta, deltax=12delta)
       θ = 2atand((r1 - r2)/x1)
       (x01, y01) = (x1 - r1*sind(θ), r1 + r1*cosd(θ))
       (x02, y02) = (-r2*sind(θ), r2 + r2*cosd(θ))
       println(θ)
       abline(x01, y01, tand(θ), -1.2, 2.2)
       segment(-1.2, 0, 2.2, 0)
       ylims!(-8delta, 2r1 + 3delta)
   end
end;

draw(2/2, true)