算額（その1395）

算額（その1395）

五六 南埼玉郡八潮町木曽根 氷川神社 安政6年(1859)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円5個，外円，三角形
#Julia, #SymPy, #算額, #和算

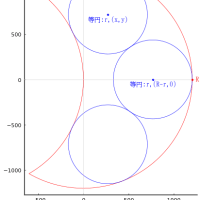
外円と三角形が交わり，隙間に全円，甲円，乙円，丙円を容れる。三角形の辺の大斜，中斜，小斜が 25 寸，20 寸，15 寸のとき，甲円の直径はいかほどか。

大斜，中斜，小斜 を a, b, c
外円の半径と中心座標を R, (0, 0)
全円の半径と中心座標を r0, (x0, y0)
甲円の半径と中心座標を r1, (x1, y1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, y3)
とおくが，本問では乙円，丙円は甲円の直径を求める上では無関係なものである。また，各円の中心座標も不要である。

径矢弦の定理は「和算の心（その009）」に書いた。
https://blog.goo.ne.jp/r-de-r/e/52facf9dc1cd8e50b191629ffa9a6c4a

using SymPy
@syms a::positive, b::positive, c::positive, s::positive, R::positive, r0::positive, r1::positive
s = (a + b + c)/2
R = (c^2 + 16r1^2)/16r1  # 径矢弦の定理
eq1 = (c/2 - s + a)^2 + (2r1 + r0 - R)^2 - (R - r0)^2  # 全円と外円が内接
eq2 = r0*s - sqrt(s*(s - a)*(s - b)*(s - c));  # 三角形の面積を二通りの方法で

res = solve([eq1, eq2], (r1, r0))[1]

   (sqrt(a + b + c)*(-a^2 + 2*a*b - b^2 + c^2)/(8*sqrt(-a^3 + a^2*b + a^2*c + a*b^2 - 2*a*b*c + a*c^2 - b^3 + b^2*c + b*c^2 - c^3)), sqrt(-a^3 + a^2*b + a^2*c + a*b^2 - 2*a*b*c + a*c^2 - b^3 + b^2*c + b*c^2 - c^3)/(2*sqrt(a + b + c)))

甲円の半径 r1 は，以下のように簡約化できる。

ans_r1 = res[1]^2 |> factor |> x -> sqrt(x)
ans_r1 |> println

   sqrt(-(a - b - c)*(a - b + c)/(a + b - c))*sqrt(a + b + c)/8

大斜，中斜，小斜が 25 寸，20 寸，15 寸のとき，甲円の直径は 5 寸である。

ans_r1(a => 25, b => 20, c => 15) |> println

   5/2

全円の半径 r0 は，以下のように簡約化できる。

ans_r0 = res[2]^2 |> factor |> x -> sqrt(x)
ans_r0 |> println

   sqrt(-(a - b - c)*(a - b + c)*(a + b - c))/(2*sqrt(a + b + c))

ans_r0(a => 25, b => 20, c => 15) |> println

   5

r1/r0 の比 p は以下のようになる。

   (a + b + c) / (4*(a + b - c))

a = 25, b = 20, c = 15 のときは p = 1/2 であるが，a, b, c が他の値のときは p も異なった値になる。

p(a => 25, b => 20, c => 15) |> println

   1/2

なお，外円の半径 R は 8.125 である。

ans_R = R(r1 => 5/2, a => 25, b => 20, c=> 15)
ans_R |> println

   8.12500000000000