算額（その239）

算額（その239）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（225-224)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

鉤股の中に全円 1 個，大円 3 個，小円 2 個がある。大円はそれぞれ部分的に重なっており，その重なった部分に小円がある。小円は大円に内接する。大円は鉤股弦に内接する。

股が 50 寸，大円の径が 15 寸，全円の径が 25 寸のとき，小円の径はいかほどか。

鉤を y，股を x，弦を z とする。全円，大円，小円の半径をそれぞれ r0, r1, r2 とする。

include("julia-source.txt");

using SymPy

@syms r2::positive, y::positive, z::positive;

x = 50
r0 = 25 // 2
r1 = 15 // 2

eq1 = x^2 + y^2 - z^2
eq2 = x + y - sqrt(x^2 + y^2) - 2r0;

鉤股弦の股と弦を求め，鉤股弦に内接する円の直径が「鉤+股-弦」になることから弦を求める。

(y, z) = solve([eq1, eq2], (y, z))[1]
(y, z) |> println

   (75/2, 125/2)

一番左の大円の中心座標 (x - (5r1 - 4r2), r1) で鉤股弦を3分割したときの鉤股弦の面積が，x*y/2 に等しいことから r2 を求める。

eq3 = x * r1 + z * r1 + (5*r1 - 4r2)y - x*y
r2 = solve(eq3, r2)[1]
r2 |> println

   5/2

小円の直径は 5 寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   x = 50
   r0 = 25 // 2
   r1 = 15 // 2
   (y, z) = (75/2, 125/2)
   r2 = 5 // 2
   plot([0, x, x, 0], [0, 0, y, 0], color=:black, lw=0.5)
   circle(x - r0, r0, r0)
   circle(x - r1, r1, r1, :green)
   circle(x - (3r1 - 2r2), r1, r1, :green)
   circle(x - (5r1 - 4r2), r1, r1, :green)
   circle(x - (2r1 - r2), r1, r2, :blue)
   circle(x - (4r1 - 3r2), r1, r2, :blue)
   if more == true
       point(x, y, " (x,y)", :black)
       point(x - r0, r0, "(x-r0,r0)", :red, :center)
       point(x - (5r1 - 4r2), 0.9r1, "(x-(5r1-4r2),r1)", :green, :center, mark=false)
       point(x - (4r1 - 3r2), 1.1r1, "(x-(4r1-3r2),r1)", :blue, :center, :bottom, mark=false)
       point(x - (5r1 - 4r2), r1, "")
       point(x - (4r1 - 3r2), r1, "", :blue)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その238）

算額（その238）

岐阜県大垣市赤坂町 金生山明星輪寺 元治2年(1865)
http://ryugen3.sakura.ne.jp/toukou3/wasankibousya.PDF

第6問　円の中に同じ半径で円弧を 2 個，その中心を通るように作り，その間に緑，赤，黄，浅青，黒円の合計 22 個の円を入れる。外側の円の直径を与えたとき，赤円の直径を求めよ。

この算額は，赤円の直径のみ求めよとなっているので，以下の算額（その55）愛宕神社のものと同じになっている。

宮城県角田市横倉 愛宕神社 明治15年(1882)1月
http://www.wasan.jp/miyagi/yokokuraatago.html

せっかくなので算額にある他の円の直径も求めてみよう。

原点を中心とする大円の半径を r0 とし，以下のように記号を定め方程式を解く。

include("julia-source.txt")

using SymPy
@syms r0, r1::positive, y1::positive, r2::positive, x2::positive, y2::positive, r3::positive;
@syms x3::positive, y3::positive;

#r0 = 1
eq1 = (r0//2)^2 +(r0//2 + r1)^2 - (r0 - r1)^2
eq2 = (r0 - r1)^2 + y1^2 - (r0 + r1)^2
res1 = solve([eq1, eq2], (r1, y1))

   2-element Vector{Tuple{Sym, Sym}}:
    (r0/6, -sqrt(6)*r0/3)
    (r0/6, sqrt(6)*r0/3)

赤円の次に大きい黄円の半径を r2, その中心座標を (x2, y2) とおき，次の連立方程式を解く。

using SymPy
@syms r0, r1::positive, x1::positive, y2::positive, r2::positive, x2::positive, y2::positive;

r0 = 1
r1 = r0//6
(x1, y1) = (r0//2, r0//2 + r1)
eq3 = (r0//2 - x2)^2 + y2^2 - (r0//2 + r2)^2 |> simplify
eq4 = (r0 - x2)^2 + y2^2 - (r0 - r2)^2 |> simplify
eq5 = (x1 - x2)^2 + (y1 - y2)^2 - (r1 + r2)^2 |> simplify
res = solve([eq3, eq4, eq5], (r2, x2, y2))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (1/11, 3/11, 6/11)
    (1/3, 1, 2/3)

最初の解が適切である。

次に，現在の円の r2, (x2, y2) がわかっているときに次の円の半径 r3，中心座標 (x3, y3) を求める漸化式を作る。上と同じ連立方程式（記号を変える）を解く。解は r2, (x2, y2) を含む式になる。

using SymPy
@syms r0, r1::positive, x1::positive, y2::positive, r2::positive, x2::positive, y2::positive,
   r3::positive, x3::positive, y3::positive;
r0 = 1
eq3 = (r0//2 - x3)^2 + y3^2 - (r0//2 + r3)^2 |> simplify
eq4 = (r0 - x3)^2 + y3^2 - (r0 - r3)^2 |> simplify
eq5 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2 |> simplify
res = solve([eq3, eq4, eq5], (r3, x3, y3))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    ((-r2^3 - 3*r2^2*x2 + 2*r2^2 + r2*x2^2 + r2*y2^2 + 3*x2^3 - 2*x2^2 + 3*x2*y2^2 + 2*y2^2 - 2*sqrt(2)*y2*sqrt(-r2^4 - r2^3 + 2*r2^2*x2^2 - 3*r2^2*x2 + 2*r2^2*y2^2 + 2*r2^2 + r2*x2^2 + r2*y2^2 - x2^4 + 3*x2^3 - 2*x2^2*y2^2 - 2*x2^2 + 3*x2*y2^2 - y2^4))/(2*(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4)), 3*(-r2^3 - 3*r2^2*x2 + 2*r2^2 + r2*x2^2 + r2*y2^2 + 3*x2^3 - 2*x2^2 + 3*x2*y2^2 + 2*y2^2 - 2*sqrt(2)*y2*sqrt(-r2^4 - r2^3 + 2*r2^2*x2^2 - 3*r2^2*x2 + 2*r2^2*y2^2 + 2*r2^2 + r2*x2^2 + r2*y2^2 - x2^4 + 3*x2^3 - 2*x2^2*y2^2 - 2*x2^2 + 3*x2*y2^2 - y2^4))/(2*(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4)), 2*y2*(-2*r2^2 - r2 + 2*x2^2 - 3*x2 + 2*y2^2 + 2)/(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4) + sqrt(2)*sqrt(-(-r2^2 - 2*r2 + x2^2 - 2*x2 + y2^2)*(-r2^2 + r2 + x2^2 - x2 + y2^2))*(r2 + 3*x2 - 2)/(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4))
    ((-r2^3 - 3*r2^2*x2 + 2*r2^2 + r2*x2^2 + r2*y2^2 + 3*x2^3 - 2*x2^2 + 3*x2*y2^2 + 2*y2^2 + 2*sqrt(2)*y2*sqrt(-r2^4 - r2^3 + 2*r2^2*x2^2 - 3*r2^2*x2 + 2*r2^2*y2^2 + 2*r2^2 + r2*x2^2 + r2*y2^2 - x2^4 + 3*x2^3 - 2*x2^2*y2^2 - 2*x2^2 + 3*x2*y2^2 - y2^4))/(2*(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4)), 3*(-r2^3 - 3*r2^2*x2 + 2*r2^2 + r2*x2^2 + r2*y2^2 + 3*x2^3 - 2*x2^2 + 3*x2*y2^2 + 2*y2^2 + 2*sqrt(2)*y2*sqrt(-r2^4 - r2^3 + 2*r2^2*x2^2 - 3*r2^2*x2 + 2*r2^2*y2^2 + 2*r2^2 + r2*x2^2 + r2*y2^2 - x2^4 + 3*x2^3 - 2*x2^2*y2^2 - 2*x2^2 + 3*x2*y2^2 - y2^4))/(2*(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4)), 2*y2*(-2*r2^2 - r2 + 2*x2^2 - 3*x2 + 2*y2^2 + 2)/(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4) - sqrt(2)*sqrt(-(-r2^2 - 2*r2 + x2^2 - 2*x2 + y2^2)*(-r2^2 + r2 + x2^2 - x2 + y2^2))*(r2 + 3*x2 - 2)/(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4))

これも，最初の式が適切である。この解に基づき，r2, x2, y2 を与えて r3, x3, y3 を得る関数にする。

nextcircle(r2, x2, y2) = ((-r2^3 - 3*r2^2*x2 + 2*r2^2 + r2*x2^2 + r2*y2^2 + 3*x2^3 - 2*x2^2 + 3*x2*y2^2 + 2*y2^2 - 2*sqrt(2)*y2*sqrt(-r2^4 - r2^3 + 2*r2^2*x2^2 - 3*r2^2*x2 + 2*r2^2*y2^2 + 2*r2^2 + r2*x2^2 + r2*y2^2 - x2^4 + 3*x2^3 - 2*x2^2*y2^2 - 2*x2^2 + 3*x2*y2^2 - y2^4))/(2*(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4)), 3*(-r2^3 - 3*r2^2*x2 + 2*r2^2 + r2*x2^2 + r2*y2^2 + 3*x2^3 - 2*x2^2 + 3*x2*y2^2 + 2*y2^2 - 2*sqrt(2)*y2*sqrt(-r2^4 - r2^3 + 2*r2^2*x2^2 - 3*r2^2*x2 + 2*r2^2*y2^2 + 2*r2^2 + r2*x2^2 + r2*y2^2 - x2^4 + 3*x2^3 - 2*x2^2*y2^2 - 2*x2^2 + 3*x2*y2^2 - y2^4))/(2*(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4)), 2*y2*(-2*r2^2 - r2 + 2*x2^2 - 3*x2 + 2*y2^2 + 2)/(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4) + sqrt(2)*sqrt(-(-r2^2 - 2*r2 + x2^2 - 2*x2 + y2^2)*(-r2^2 + r2 + x2^2 - x2 + y2^2))*(r2 + 3*x2 - 2)/(r2^2 + 6*r2*x2 - 4*r2 + 9*x2^2 - 12*x2 + 8*y2^2 + 4));

この関数を使えば r1 = 1/6 から順次 r2, r3,... を求めることができる。

r1 = 1/6 から始まる類円は，r2 = 1/11, r3 = 1/18, r4 = 1/27... である。

n 番目の類縁の半径の一般項は n^2 + 2n + 3 である。

各円の中心座標を求めて図を描く。

   r0 = 1.00000;  r1 = 0.16667;  x1 = 0.16667;  y1 = 0.81650
    1  (0.16666666666666666,  0.5,                  0.6666666666666666)   1/r1 = 6.0
    2  (0.0909090909090909,   0.27272727272727265,  0.5454545454545454)   1/r2 = 11.000000000000002
    3  (0.05555555555555554,  0.1666666666666666,   0.44444444444444436)  1/r2 = 18.000000000000007
    4  (0.037037037037037014, 0.11111111111111105,  0.37037037037037024)  1/r2 = 27.000000000000018
    5  (0.026315789473684195, 0.07894736842105259,  0.31578947368421045)  1/r2 = 38.00000000000002
    6  (0.01960784313725489,  0.05882352941176468,  0.2745098039215686)   1/r2 = 51.00000000000003
    7  (0.015151515151515148, 0.04545454545454544,  0.24242424242424243)  1/r2 = 66.00000000000001
    8  (0.012048192771084336, 0.03614457831325301,  0.21686746987951808)  1/r2 = 83.00000000000001
    9  (0.00980392156862745,  0.029411764705882353, 0.19607843137254902)  1/r2 = 102.0
   10  (0.008130081300813007, 0.024390243902439025, 0.17886178861788618)  1/r2 = 123.00000000000001
   11  (0.006849315068493151, 0.020547945205479454, 0.1643835616438356)   1/r2 = 146.0

using Plots
using Printf

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r0 = 1
   (r1, y1) = (r0/6, sqrt(6)*r0/3)
   @printf("r0 = %.5f;  r1 = %.5f;  x1 = %.5f;  y1 = %.5f\n", r0, r1, r1, y1)
   plot()
   circle(0, 0, r0, :green)
   circle(r0, 0, r0, :green, beginangle=120, endangle=240)
   circle(-r0, 0, r0, :green, beginangle=300, endangle=420)
   circle(r0/2, r0/2 + r1, r1, :magenta)
   circle(-r0/2, r0/2 + r1, r1, :magenta)
   circle(r0/2, -r0/2 - r1, r1, :magenta)
   circle(-r0/2, -r0/2 - r1, r1, :magenta)
   circle(r1, y1, r1, :magenta)
   circle(-r1, y1, r1, :magenta)
   circle(r1, -y1, r1, :magenta)
   circle(-r1, -y1, r1, :magenta)
   circle(r0/2, 0, 1/2, :blue)
   circle(-r0/2, 0, 1/2, :blue)
   if more
       point(r1, sqrt(6)*r0/3, "(r1,y1)", :magenta, :center)
       point(r0/2, r0/2+r1, "(r0/2,r0/2+r1)", :magenta, :center)
       point(r0/2, 0, " r0/2", :blue)
       point(0, 0, " 0", :black)
       point(r0, 0, " r0", :black)
       #point(x2, y2, "(x2,y2)")
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
   end
   (x1, y1) = (r0/2, r0/2 + r1)
   println("1  ", (r1, x1, y1), "  1/r1 =$(1/r1)")
   for i = 1:10
       (r2, x2, y2) = nextcircle(r1, x1, y1)
       println("$(i+1)  ", (r2, x2, y2), "  1/r2 =$(1/r2)")
       circle(x2, y2, r2, i)
      (r1, x1, y1) = (r2, x2, y2)
   end  
end;

算額（その237）

算額（その237）

七四 加須市大字外野 棘脱地蔵堂 明治7年(1874)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

山形県南原町 熊野神社
山形算額勝負-湯殿山神社を目指せ-
https://www.sci.yamagata-u.ac.jp/wasan/pdf/20180711SSEP.pdf

外円内に大円 2 個，小円 2 個が入っている。大円の径が 3寸のとき，小円の径はいかほどか。

算額の図では左右対称に見えないが，条件からすると左右対称でしかありえない。 すなわち，外円の中心を原点に置くと，小円の中心は x 座標軸上，大円の中心は y 座標軸上にあるべき。

外円の中心を原点(0, 0) におき，半径を r0 とする。 大円の半径を r1 とし，中心座標を (0, r1) に置く。r1 = r0/2 である。 小円の半径を r2 とし，中心座標を (r0 - r2, 0) とする。 以下の方程式を解く。

include("julia-source.txt")

using SymPy

@syms r0, r1, r2
r1 = 3//2
eq0 = r1 - r0//2
eq1 = (r0 - r2)^2 + r1^2 - (r1 + r2)^2
solve([eq0, eq1], (r0, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (3, 1)

外円の直径は 6 寸，小円の直径は 2 寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r2) = (3, 1)
   @printf("小円の直径 = %.7f\n", 2r2)
   plot()
   circle(0, 0, r0, :black)
   circle(0, r1, r1, :green)
   circle(0, -r1, r1, :green)
   circle(r0 - r2, 0, r2)
   circle(-r0 + r2, 0, r2)
   if more == true
       point(0, r1, " r1")
       point(r1/2, 1.2r1, "大円", mark=false)
       point(r0 - r2, 0, " r0-r2", :red)
       point(r0 - r2, 0.5r2, "小円", :red, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

和算の心（その002）

和算の心（その002）

算額の問題を解くための定石をまとめておく。

山形県南原町 熊野神社
山形算額勝負-湯殿山神社を目指せ-
https://www.sci.yamagata-u.ac.jp/wasan/pdf/20180711SSEP.pdf

直線の上に直径 9寸の大円，直径 4寸の小円があり，互いに接している。大円と小円の接点間の距離（子*¹）はいくつか。
注1: 和算では変数名として，子，丑，寅... を使う。

大円と小円の半径および中心の x 座標をそれぞれ r_big，r_small， x_big，x_small とおく。二円が外接することに関する方程式を解く。

include("julia-source.txt")

using SymPy

@syms r_big::positive, x_big::positive, r_small::positive, x_small::positive, ne::positive

eq = ne^2 + (r_big - r_small)^2 - (r_big + r_small)^2
res = solve(eq, ne)[1]
println("距離（子） = $(res)")

r_big = 9//2
r_small = 4//2
距離 = 2*sqrt(r_big)*sqrt(r_small)
距離 |> println

   6.0

求める距離は 2√(大円の半径 * 小円の半径） である。すなわち，直径 9寸の大円，直径 4寸の小円の場合は 2√(4.5*2) = 6 である。元の単位では 6 寸。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r_big, r_small) = (9, 4) .// 2
   x_big = 0
   ne = 2√(r_big * r_small)
   x_small = x_big + ne
   @printf("r_big = %.7f;  r_small = %.7f\n", r_big, r_small)
   @printf("子 = %.7f\n", 2√(r_big * r_small))
   plot()
   circle(0, r_big, r_big)
   circle(ne, r_small, r_small, :blue)
   hline!([0], color=:black, lw=0.5)
   if more == true
       point(0, r_big, " r_big")
       point(x_small, r_small, "(x_small,r_small)", :blue, :center)
       point(x_small, 0, "子\n", :blue, :center, :bottom)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

AI の活用？？

AI活用のルール

 

 

ChatGPT

 

AIの活用には、以下のようなルールが存在します。

1. 倫理と法律の尊重: AIの活用は、倫理的な観点や法的な制約を尊重する必要があります。人権やプライバシーの侵害を防ぐために、関連する法律や規制に従うことが重要です。

2. 透明性と説明責任: AIシステムが意思決定や推論を行う場合、そのプロセスや基準を透明にする必要があります。ユーザーや関係者に対して説明責任を果たすことで、信頼性と責任を確保します。

3. データの正確性と公平性: AIのトレーニングに使用するデータは、正確性と公平性が確保されている必要があります。バイアスのないデータセットを使用し、アルゴリズムの結果が公正であることを確認するために、定期的な監査や評価を実施することが重要です。

4. プライバシーとセキュリティの保護: AIに関連するデータは、適切なセキュリティ対策を講じて保護されるべきです。個人情報や機密情報の取り扱いには特に注意が必要であり、データの不正利用や漏洩を防ぐための措置を講じることが必要です。

5. 人間との協働: AIは人間の補完として活用されるべきです。人間とAIの協力によって相互補完的な強みを引き出し、より効果的な結果を生み出すことが期待されます。AIは人間の意思決定をサポートし、自動化されたプロセスにおける人間の監視や介入が必要な場合もあります。

6. 継続的なモニタリングと改善: AIシステムのパフォーマンスや影響を継続的に監視し、必要に応じて改善を行うことが重要です。フィードバックの収集やモデルのアップデートを通じて、AIの正確性や効果性を向上させる取り組みを行います。

これらのルールは、AIの活用において倫理的な枠組みを提供し、AIシステムが社会的な価値を提供するため

るとともに、リスクや潜在的な問題を最小限に抑える役割を果たします。AIの活用には、これらのルールを遵守し、適切なガバナンスと監督を確立することが重要です。

また、AIの活用に関しては、以下のような考慮事項も重要です。

1. ユーザーのインクルージョン: AIシステムは、ユーザーの多様なニーズや能力に対応する必要があります。アクセシビリティやユーザビリティの観点から、利用者がシステムを理解し、利用できるように設計されるべきです。

2. 信頼性と責任: AIの活用は、高い信頼性と責任を持つことが求められます。アルゴリズムの誤った判断や結果による悪影響を最小限に抑えるために、信頼性の確保と責任ある運用が必要です。

3. フェアネスと公正性: AIの活用は、公正でバイアスのない結果を提供することが重要です。特定の個人やグループに対する差別や不平等を生じないよう、アルゴリズムの設計やトレーニングデータの選択において公正性を確保する必要があります。

4. 透明性と説明可能性: AIの意思決定プロセスが透明で説明可能であることは重要です。ユーザーにとって理解可能であり、必要な場合には説明ができるようなAIシステムの設計と運用が求められます。

5. 知識の更新と学習: AIの活用には、最新の知識や技術の継続的な学習が不可欠です。迅速な変化や新たな課題に対応するために、AIシステムの開発者や利用者は常に学習し、技術を進化させる努力を続ける必要があります。

これらのルールと考慮事項に基づいて、AIの活用は社会的な利益を最大化し、持続可能な発展に貢献することが期待されます。

算額（その236）

算額（その236）

山形県南原町 熊野神社
山形算額勝負-湯殿山神社を目指せ-
https://www.sci.yamagata-u.ac.jp/wasan/pdf/20180711SSEP.pdf

鉤股の中に菱形，大円，中円，小円が入っている。股が 36 寸，弦が 45 寸のとき，菱形の辺の長さおよび大円，中円，小円の直径を求めよ。

菱形の辺の長さを z，鉤をx，小円が入っている鉤股弦の鉤および股を y，36 - z，中円が入っている鉤股弦の鉤を x - y とする。
以下の方程式を解く。

include("julia-source.txt")

using SymPy

@syms x::positive, y::positive, z::positive;
eq1 = x^2 + 36^2 - 45^2
eq2 = 36*(x - y) - x*z
eq3 = y^2 + (36 - z)^2 - z^2
(x, y, z) = solve([eq1, eq2, eq3], (x, y, z))[1]

   (27, 12, 20)

鉤股弦に内接する円の直径は，「鉤+股-弦」である。

大円，中円，小円の直径を R1, R2, R3 とすると以下の通り。

R1 = x + 36 - 45
R2 = (x - y) + z - (45 - z)
R3 = y + (36 - z) - z
println((R1, R2, R3))

   (18, 10, 8)

   x = 27.0000000;  y = 12.0000000;  z = 20.0000000
   r1 = 9.0000000;  r2 = 5.0000000;  r3 = 4.0000000

菱形の一辺の長さは 20寸，大円，中円，小円の直径はそれぞれ 18寸，10寸，8寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   # 大円，中円，小円の半径を r1, r2, r3 とする
   (x, y, z, r1, r2, r3) = (27, 12, 20, 18/2, 10/2, 8/2)
   @printf("x = %.7f;  y = %.7f;  z = %.7f\n", x, y, z)
   @printf("r1 = %.7f;  r2 = %.7f;  r3 = %.7f\n", r1, r2, r3)
   plot([0, 36, 0, 0], [0, 0, x, 0], color=:black, lw=0.5)
   plot!([z, 0, 36 - z], [y, y, 0], color=:black, lw=0.5)
   circle(r1, r1, r1)
   circle(r2, y + r2, r2, :green)
   circle(r3, r3, r3, :blue)
   if more == true
       point(0, x, "x ", :green, :right)
       point(0, y, "y ", :green, :right)
       point(36 - z, 0, "36 - z", :green, :left, :bottom)
       point(36, 0, " 36", :green, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       plot!(showaxis=false)
   else
       plot!(showaxis=false)
   end
end;

算額（その235）

算額（その235）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（225-226)
長野県諏訪市下諏訪 諏訪大社下社 慶応4年(1868)

菱形の中に一辺約 8寸5分5厘2毛6糸あまりの正方形が入っている。菱形の対角線(長い方と短い方）の長さを求めよ。

対角線の長さを，x, y，正方形の一辺の長さを a とおく。

三角形の相似関係で，AD/DE = AB/BC これは (y - a)/a = y/x である。

a について解くと，a = x*y / (x + y) となる。

include("julia-source.txt")

using SymPy

@syms x::positive, y::positive, a::positive;
@syms x, y, a
eq = (y - a)/a - y/x
solve(eq, a)[1] |> println

   x*y/(x + y)

x, y を整数として，x*y / (x + y) ≒ 8.5526寸になるものを探索する。なお，小数なので 1万倍して切り捨てたときに 85526 になるものを解とする。

1 < y < x < 10000000 までを探索してみる。この範囲内では条件を満たすのは，x = 25, y = 13 の場合のみであり，そのときの正方形の一辺の長さは 25*13/(25+13) = 8.552631578947368 であり，題意を満たしていることが確認できる。

正方形の一辺の長さが整数値になる x, y の組み合わせもあるが，解の一意性を保証するために「8.5526寸あまり」という半端な数を指定している。

a = 85526
limit = 10000000
for x in 1:limit
   for y in 1:x
       res = floor(x*y / (x + y) * 10000)
       if res > a
           break
       elseif res == a
           println("x = $x;  y = $y")
       end
   end
end

   x = 25;  y = 13

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x, y) = [25, 13] / 2
   a = 8.5526 / 2
   plot([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:black, lw=0.5)
   rect(-a, -a, a, a)
   if more == true
       point(0, y, " A", :black, :left, :bottom)
       point(0, 0, " B", :black, :left, :bottom)
       point(x, 0, " C", :black, :left, :bottom)
       point(0, a, " D", :black, :left, :bottom)
       point(a, a, " E", :black, :left, :bottom)
       point(a, 0, " F", :black, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       plot!(showaxis=false)
   else
       plot!(showaxis=false)
   end
end;

算額（その234）

算額（その234）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（223)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

算額（その4）を一段階複雑にしたものである。https://blog.goo.ne.jp/r-de-r/e/faa0efc125cc1b246538a9965949f782

正三角形と甲円，乙円，丙円，丁円がある。乙円，丁円の径がそれぞれ 16寸，9寸のとき，丙円の径を求めよ。

甲円の半径 r1, (0, 2r3 + r1),
乙円の半径 r2, (x2, r2),
丙円の半径 r3, (r3, r3),
丁円の半径 r4, (x4, y4), 
だたし，r2 = 16/2, r4 = 9/2
また，x4, y4 は r1, r3 から求めることができる

以下の方程式を解き，r1, r3, x2 を求める。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, r3::positive, r4::positive,
     x2::positive;

(r2, r4) = (16//2, 9//2)
eq1 = x2^2 + (r2 - r3)^2 - (r2 + r3)^2
eq2 = x2^2 + (2r3 + r1 - r2)^2 - (r1 + r2)^2
eq3 = r1 / 2 - 2r4;
solve([eq1, eq2, eq3], (r1, r3, x2))[1]

   (18, 6, 8*sqrt(3))

(r1, r3, x2) = (18, 6, 8*sqrt(3))

   (18, 6, 13.856406460551018)

ついで，x4, y4 を求める。

x4 = (r1*(3/4))*sqrt(3)/2
y4 = 2r3 + r1 + (r1*(3/4))/2
(x4, y4)

   (11.69134295108992, 36.75)

r1 = 18, r3 = 6, x2 = 13.8564065;  x4 = 11.6913430;  y4 = 36.75
丙円の半径 r3 = 6 なので，元の単位での直径は 12 寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3, x2) = (18, 6, 8*sqrt(3))
   x4 = (r1*(3/4))*sqrt(3)/2
   y4 = 2r3 + r1 + (r1*(3/4))/2
   @printf("r1 = %.7f;  r3 = %.7f;  x2 = %.7f\n", r1, r3, x2)
   @printf("x4 = %.7f;  y4 = %.7f\n", x4, y4)
   y = 2r3 + 2r1
   x = y/sqrt(3)
   plot([x, 0, -x, x], [0, y, 0, 0], color=:black, lw=0.5)
   circle(0, 2r3 + r1, r1, :red)
   circle(x2, r2, r2, :green)
   circle(-x2, r2, r2, :green)
   circle(0, r3, r3, :blue)
   circle(x4, y4, r4, :gold)
   circle(-x4, y4, r4, :gold)
   if more == true
       point(0, 2r3 + r1, " 2r3+r1", :red)
       point(0, 2r3 + r1, " 甲円", :red, :left, :bottom)
       point(0, 2r3 + 2r1, " 2r3+2r1", :black, :left, :bottom)
       point((2r3 + 2r1)/√3, 0, "(2r3+2r1)/√3 ", :black, :right, :bottom)
       point(x4, y4, "(x4,y4)", :gold, :center)
       point(x4, y4, "丁円", :gold, :center, :bottom)
       point(0, r3, " r3", :blue)
       point(0, r3, " 丙円", :blue, :left, :bottom)
       point(x2, r2, "(x2,r2)", :green, :center)
       point(x2, r2, "乙円", :green, :center, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その233）

算額（その233）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（222)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

菱形の中に，大円，中円，小円が入っている。中円，小円の径がそれぞれ 8寸，4寸のとき，大円の径を求めよ。

大円の半径 r1, (r3 + r1, 0),
中円の半径 r2, (0, r3 + r2),
小円の半径 r3, (0, 0),
だたし，r2 = 8/2, r3 = 4/2。
以下の方程式を解く。

r2, r3 が与えられているとき，条件式は 1 つである。
r2, r3 が任意の値を取るとしてこの方程式を解くと r1 は r2, r3 を含む式になる。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, r3::positive;

(r2, r3) = (4, 2)
eq1 = (r3 + r1)^2 + (r3 + r2)^2 - (r1 + r2)^2
solve(eq1, r1)[1] |> println

   r3*(r2 + r3)/(r2 - r3)

すなわち，「中円と小円の半径の和を，中円と小円の半径の差で割り，小円の半径を掛ければ，大円の半径が得られる」
2 * (4 + 2) / (4 - 2) = 6 である。

大円の半径は6，すなわち元の単位での大円の直径は 12寸である。

外形の菱形を書くには，x軸上の頂点のx座標を x, y軸上の頂点のx座標を y として方程式を2本追加し，合わせて3本の連立方程式を解く。

ただし，r2, r3 が未知数のままだと solve() では解を求めることができないので，問にあるように r2 = 4, r3 = 2 の場合について解く。

using SymPy
@syms r1::positive, r2::positive, r3::positive, x::positive, y::positive;

(r2, r3) = (4, 2)
eq1 = (r3 + r1)^2 + (r3 + r2)^2 - (r1 + r2)^2
eq2 = distance(0, y, x, 0, r3 + r1, 0) - r1^2
eq3 = distance(0, y, x, 0, 0, r3 + r2) - r2^2;

res = solve([eq1, eq2, eq3], (r1, x, y))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (6, (13*sqrt(6) + 32)/(2*sqrt(7 - 2*sqrt(6))), 26/5 + 32*sqrt(6)/15)

x はもう少し簡単な式になる。

res[1][2] |> sympy.sqrtdenest |> simplify |> println

   11 + 9*sqrt(6)/2

y は通分ぐらいしか手がない。

res[1][3] |> factor |> println

   2*(39 + 16*sqrt(6))/15

   r1 = 6.0000000
   x = 22.0227038;  y = 10.4255781

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, x, y) = (6, 11 + 9*sqrt(6)/2, (78 + 32*sqrt(6))/15)
   @printf("r1 = %.7f\n", r1)
   @printf("x = %.7f;  y = %.7f\n", x, y)
   plot([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:black, lw=0.5)
   circle(r3 + r1, 0, r1, :red)
   circle(-r3 - r1, 0, r1, :red)
   circle(0, r3 + r2, r2, :blue)
   circle(0, -r3 - r2, r2, :blue)
   circle(0, 0, r3, :green)
   if more == true
       point(r3, 0, " r3", :green)
       point(0, 0, "小円", :green, :center, :top, mark=false)
       point(r3 + r1, 0, " r3+r1", :red)
       point(r3 + r1, r3, "大円", :red, mark=false)
       point(x, 0, " x", :black)
       point(0, r3 + r2, "r3+r2", :blue, :right, :bottom)
       point(0, r3 + r2, " 中円", :blue, :left, :bottom, mark=false)
       point(0, y, "y ", :black, :right, :bottom)
       point(0, r3, "r3", :blue, :right, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その232）

算額（その232）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（222)
長野県東筑摩郡筑北村青柳 碩水寺豊川稲荷社 慶応4年(1868)

団扇の中に大円 2 個、小円 １ 個がある。扇の径が 9 寸、大円の径が 4寸5分のとき、小円の径はいかほどか。

大円の半径と中心座標を r1, (x1, y1), r1 = r0//2, y1 = 0
小円の半径と中心座標を r2, (0, r0 - r2)
団扇面を切り欠く円の中心座標を (0, y), y < 0
団扇面の円と扇面を切り欠く円の交点座標を (x0, y0)
とし，連立方程式を解く。
なお，団扇面を切り欠く円の半径，中心については条件式が与えられていないので解は y を含む式になる。

include("julia-source.txt")

using SymPy
@syms r0::positive, r1::positive, y1,
     r2::pisitive, r::positive, y::negative,
     x0::positive, y0::negative;
r0 = 9 
r1 = r0 // 2
y1 = 0
y0 = -sqrt(r0^2 - x0^2)
eq1 = r1^2 + (r0 - r2 -y1)^2 - (r1 + r2)^2
eq3 = r1^2 + (y1 - y)^2 - (r + r1)^2
eq5 = sqrt(r^2 - x0^2) + y + sqrt(r0^2 - x0^2)
res = solve([eq1, eq3, eq5], (r2, r, x0))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (3, sqrt(4*y^2 + 81)/2 - 9/2, -9*sqrt(12*y^2 - 18*sqrt(4*y^2 + 81) - 162)/(4*y))

たとえば y = -9 のとき，
r2 = 3
r  = 5.562305898749054
x0 = 5.2900672706322585
になる。

y = -9
(3, sqrt(4*y^2 + 81)/2 - 9/2, -9*sqrt(12*y^2 - 18*sqrt(4*y^2 + 81) - 162)/(4*y))

   (3, 5.562305898749054, 5.2900672706322585)

   小円半径 = 3.00000
   団扇面の円を切り欠く円の中心 = (0, -9.00000);  半径 = 5.56231
   2円の交点 = (5.29007, -7.28115)

using Printf
using Plots

function draw(y, more)
   pyplot(size=(500, 500), grid=false, aspect_ratio=1, label="", fontfamily="IPAMincho")
   r0 = 9 
   r1 = 9//2
   y1 = 0
   (r2, r, x0) = (3, sqrt(4*y^2 + 81)/2 - 9/2, -9*sqrt(12*y^2 - 18*sqrt(4*y^2 + 81) - 162)/(4*y))
   y0 = -sqrt(r0^2 - x0^2)
   @printf("小円半径 = %.5f\n", r2)
   @printf("団扇面の円を切り欠く円の中心 = (0, %.5f);  半径 = %.5f\n", y, r)
   @printf("2円の交点 = (%.5f, %.5f)\n", x0, y0)
   θ = Int(round(atand((y0 - y)/x0), digits=0))
   plot()
   circle(0, 0, r0, :black)
   circle(0, r0 - r2, r2)
   circle(r1, y1, r1, :blue)
   circle(-r1, y1, r1, :blue)
   circle(0, y, r, :black, beginangle=θ, endangle=180 - θ)
   for deg = 90:10:180-θ
       plot!([-r*cosd(deg), 0, r*cosd(deg)], [r*sind(deg) + y, -r0, r*sind(deg) + y], color=:black, lw=2)
   end
   if more
       point(0, r0, " r0", :black, :left, :bottom)
       point(0, r0 - r2, " r0-r2", :red, :left, :bottom)
       point(x0, y0, "(x0,y0)")
       point(r1, y1, " r1", :blue)
       point(r0, y1, " r0 ", :black, :right)
       point(0.2r1, (2r0 - r2)/2, "小円", :red, mark=false)
       point(r1, r1/2, "大円", :blue, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その231）

算額（その231）

福島県郡山市西田町丹伊田字宮作239番地 鹿島大神宮 令和3年 武田健司さんが奉納
https://kashimadaijingu.jp/archives/2785.html

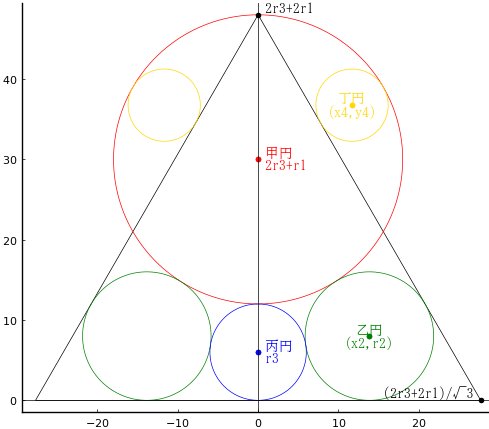
半径 1 の 2 つの円が，互いの中心を通り重なり合っている。その中に 27 個の円が図のように接している。2 つの円が作る領域から，27個の円を除いた領域の面積を求めよ。

交差する 2 つの円の半径を 1 とする。
x軸上に並ぶ 3 個の円（円1）の半径を r1 とする。r1 = 1/2 である。中心座標は左から順に (-2r1, 0), (0, 0), (2r1, 0)
ついで半径の大きい順に 半径，中心座標を以下のように定める。
円2: r2, (x2, y2),
円3: r3, (0, r1 + r3),
円4: r4, (x4, y4),
円5: r5, (x5, y5),
円6: r6, (x6, y6),
円7: r7, (x7, y7),
円8: r8, (0, r1 + 2r3 + r8)
以下の方程式を解く。

using SymPy

@syms r1::positive,
   r2::positive, x2::positive, y2::positive,
   r3::positive,
   r4::positive, x4::positive, y4::positive,
   r5::positive, x5::positive, y5::positive,
   r6::positive, x6::positive, y6::positive,
   r7::positive, x7::positive, y7::positive,
   r8::positive;

r1 = 1//2

eq01 = r1^2 + (r1 + 2r3 + r8)^2 - (2r1 - r8)^2  # 右外円に円8が内接
eq02 = r1^2 + (r1 + r3)^2 - (2r1 - r3)^2        # 右外円に円3が内接

eq03 = x6^2 + (r1 + r3 - y6)^2 - (r3 + r6)^2    # 円3と円6が外接
eq04 = x6^2 + y6^2 - (r1 + r6)^2                # 中円1と円6が外接
eq05 = (x6 + r1)^2 + y6^2 - (2r1 - r6)^2        # 左外円に円6が内接

eq06 = (x2 - r1)^2 + y2^2 - (2r1 - r2)^2        # 右外円に円2が内接
eq07 = (x2 + r1)^2 + y2^2 - (2r1 + r2)^2        # 左外円と円2が外接
eq08 = (2r1 - x2)^2 + y2^2 - (r1 + r2)^2        # 右円1と円2が外接

eq09 = (x4 - r1)^2 + y4^2 - (2r1 - r4)^2        # 右外円に円4が内接
eq10 = (x4 -2r1)^2 + y4^2 - (r1 + r4)^2         # 右円1と円4が外接
eq11 = (x4 - x2)^2 + (y2 - y4)^2 - (r2 + r4)^2  # 円2と円4が外接

eq12 = (x5 - r1)^2 + y5^2 - (2r1 - r5)^2        # 右外円に円5が内接
eq13 = (x2 - x5)^2 + (y5 - y2)^2 - (r2 + r5)^2  # 円2と円5が外接
eq14 = (x5 + r1)^2 + y5^2 - (2r1 + r5)^2        # 左外円と円5が外接

eq15 = (x7 - r1)^2 + y7^2 - (2r1 - r7)^2        # 右外円に円7が内接
eq16 = (x7 + r1)^2 + y7^2 - (2r1 + r7)^2        # 左外円と円7が外接
eq17 = (x5 - x7)^2 + (y7 - y5)^2 - (r5 + r7)^2; # 円5と円7が外接

res = solve([eq01, eq02,  eq03, eq04, eq05,  eq06, eq07, eq08,  eq09, eq10, eq11,  eq12, eq13, eq14,  eq15, eq16, eq17],
   (r2, x2, y2, r3, r4, x4, y4, r5, x5, y5, r6, x6, y6, r7, x7, y7, r8))

   4-element Vector{NTuple{17, Sym}}:
    (3/10, 3/5, 2*sqrt(3)/5, 1/6, 39/121 - 12*sqrt(3)/121, 36*sqrt(3)/121 + 129/242, 30/121 + 28*sqrt(3)/121, 9/82, 9/41, 20*sqrt(3)/41, 1/11, 5/22, 6/11, 27/730, 27/365, 182*sqrt(3)/365, 1/66)
    (3/10, 3/5, 2*sqrt(3)/5, 1/6, 39/121 - 12*sqrt(3)/121, 36*sqrt(3)/121 + 129/242, 30/121 + 28*sqrt(3)/121, 9/82, 9/41, 20*sqrt(3)/41, 1/11, 5/22, 6/11, 3/10, 3/5, 2*sqrt(3)/5, 1/66)
    (3/10, 3/5, 2*sqrt(3)/5, 1/6, 12*sqrt(3)/121 + 39/121, 129/242 - 36*sqrt(3)/121, -30/121 + 28*sqrt(3)/121, 9/82, 9/41, 20*sqrt(3)/41, 1/11, 5/22, 6/11, 27/730, 27/365, 182*sqrt(3)/365, 1/66)
    (3/10, 3/5, 2*sqrt(3)/5, 1/6, 12*sqrt(3)/121 + 39/121, 129/242 - 36*sqrt(3)/121, -30/121 + 28*sqrt(3)/121, 9/82, 9/41, 20*sqrt(3)/41, 1/11, 5/22, 6/11, 3/10, 3/5, 2*sqrt(3)/5, 1/66)

1 番目の解が妥当なものである。

names = ("r2", "x2", "y2", "r3", "r4", "x4", "y4", "r5", "x5", "y5", "r6", "x6", "y6", "r7", "x7", "y7", "r8")
for i = 1:17
   println("$(names[i]) = $(res[1][i]) = $(res[1][i].evalf())")
end

   r2 = 3/10 = 0.300000000000000
   x2 = 3/5 = 0.600000000000000
   y2 = 2*sqrt(3)/5 = 0.692820323027551
   r3 = 1/6 = 0.166666666666667
   r4 = 39/121 - 12*sqrt(3)/121 = 0.150540415778293
   x4 = 36*sqrt(3)/121 + 129/242 = 1.04837875266512
   y4 = 30/121 + 28*sqrt(3)/121 = 0.648739029850649
   r5 = 9/82 = 0.109756097560976
   x5 = 9/41 = 0.219512195121951
   y5 = 20*sqrt(3)/41 = 0.844902832960428
   r6 = 1/11 = 0.0909090909090909
   x6 = 5/22 = 0.227272727272727
   y6 = 6/11 = 0.545454545454545
   r7 = 27/730 = 0.0369863013698630
   x7 = 27/365 = 0.0739726027397260
   y7 = 182*sqrt(3)/365 = 0.863652731445303
   r8 = 1/66 = 0.0151515151515152

円1〜円8 の円の面積（ひとつあたり）

s = PI .* [r1, res[1][1], res[1][4], res[1][5], res[1][8], res[1][11], res[1][14], res[1][17]].^2
s |> println

   Sym[pi/4, 9*pi/100, pi/36, pi*(39/121 - 12*sqrt(3)/121)^2, 81*pi/6724, pi/121, 729*pi/532900, pi/4356]

図中にある個数

num = [3, 4, 2, 4, 4, 4, 4, 2]

   8-element Vector{Int64}:
    3
    4
    2
    4
    4
    4
    4
    2

図中にある全ての円の面積の和

S1 = sum(s .* num).evalf()
S1 |> println

   4.22035198660619

二円の構成する面積。第1象限の面積の 4 倍

@syms x
S2 = integrate(sqrt(4r1^2 - (x - r1)^2), (x, 0, 3r1)).evalf() * 4
S2 |> println

   5.05481560857083

二円の構成する面積から全ての円の面積の和を引いたもの

S2 - S1 |> println

   0.834463621964642

using Plots
using Printf

function circle4(x, y, r, color=:red; fill=false)
    circle(x, y, r, color, fill=fill)
    circle(x, -y, r, color, fill=fill)
    circle(-x, y, r, color, fill=fill)
    circle(-x, -y, r, color, fill=fill)
end;

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
    θ = beginangle:0.1:endangle
    x = r.*cosd.(θ)
    y = r.*sind.(θ)
    if fill
        plot!(ox .+ x, oy .+ y, linecolor=:black, linewidth=0.5, seriestype=:shape, fillcolor=:black)
    else
        plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
    end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
    mark && scatter!([x], [y], color=color, markerstrokewidth=0)
    annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more; fill=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r1 = 1/2
    (r2, x2, y2, r3, r4, x4, y4, r5, x5, y5, r6, x6, y6, r7, x7, y7, r8) = res[1]
    @printf("r1 = %.7f\n", r1)
    @printf("r2 = %.7f;  x2 = %.7f;  y2 = %.7f\n", r2, x2, y2)
    @printf("r3 = %.7f\n", r3)
    @printf("r4 = %.7f;  x4 = %.7f;  y4 = %.7f\n", r4, x4, y4)
    @printf("r5 = %.7f;  x5 = %.7f;  y5 = %.7f\n", r5, x5, y5)
    @printf("r6 = %.7f;  x6 = %.7f;  y6 = %.7f\n", r6, x6, y6)
    @printf("r7 = %.7f;  x7 = %.7f;  y7 = %.7f\n", r7, x7, y7)
    @printf("r8 = %.7f\n", r8)
    plot()
    circle(r1, 0, 2r1, :red)
    circle(-r1, 0, 2r1, :red)
    circle(0, 0, r1, :green, fill=fill)
    circle(2r1, 0, r1, :green, fill=fill)
    circle(-2r1, 0, r1, :green, fill=fill)
    circle(0, r1 + r3, r3, fill=fill)
    circle(0, -r1 - r3, r3, fill=fill)
    circle(0, r1 + 2r3 + r8, r8, :black, fill=fill)
    circle(0, -r1 - 2r3 - r8, r8, :black, fill=fill)
    circle4(x2, y2, r2, :gold, fill=fill)
    circle4(x4, y4, r4, :magenta, fill=fill)
    circle4(x5, y5, r5, :blue, fill=fill)
    circle4(x6, y6, r6, :darkorange3, fill=fill)
    circle4(x7, y7, r7, :cyan4, fill=fill)
    if more == true
        point(0, 0, "0 ", :green, :right)
        point(r1, 0, "r1 ", :green, :right)
        point(2r1, 0, "2r1 ", :green, :right)
        point(3r1, 0, "3r1 ", :green, :right)
        point(2r1, r1/3, "円1", :green, mark=false)
        point(x2, y2, "円2", :gold, mark=false)
        point(0, r1 + r3, "円3", :red, mark=false)
        point(x4, y4, "円4", :magenta, mark=false)
        point(x5, y5, "円5", :blue, mark=false)
        point(x6, y6, "円6", :darkorange3, mark=false)
        point(x7, y7, "円7", :cyan4, mark=false)
        point(0, r1 + 2r3 + 7r8, "円8", :black, :center, :bottom, mark=false)
        hline!([0], color=:black, lw=0.5)
        vline!([0], color=:black, lw=0.5)
    else
        plot!(showaxis=false)
    end
end;

算額（その230）

算額（その230）

(12) 京都市伏見区御香宮門前町 御香宮神社（ごこうのみやじんじゃ）文久3年(1863)
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

絵馬堂が意外におもしろい！（3）　－ 御香宮神社 －
http://flattravel.blog.fc2.com/blog-entry-16.html

キーワード：円3個，長方形

大円の一部を欠き取る長方形内に，天円と地円を入れる。長方形の長辺と短辺がそれぞれ 4寸，3寸で，大円の径が 13寸のとき，天円と地円の径はいかほどか。

長方形の左下角の座標を (x, y) とおく。
大円の半径，中心座標を r0, (0, 0)
天円の半径，中心座標を r1, (x1, y1) # (x + r1, y + 3 - r1)
地円の半径，中心座標を r2, (x2, y2) # (x + 4 - r2, y + r2)
とおき，以下の方程式を解く。
注: x, x1, x2 は ::negative である。

using SymPy

@syms r0::positive, x::negative, y::positive,
   r1::positive, x1::negative, y1::positive,
   r2::positive, x2::negative, y2::positive;
r0 = 13//2
(x1, y1) = (x+r1, y + 3 - r1)
(x2, y2) = (x + 4 - r2, y + r2)
eq1 = x1^2 + y1^2 - (r0 + r1)^2
eq2 = x2^2 + y2^2 - (r0 - r2)^2
eq3 = x^2 + y^2 - r0^2
eq4 = (x + 4)^2 + (y + 3)^2 - r0^2

res = solve([eq1, eq2, eq3, eq4], (r1, r2, x, y))

   2-element Vector{NTuple{4, Sym}}:
    (4/5, 6/5, -28/5, 33/10)
    (36, 6/5, -28/5, 33/10)

最初の解が妥当なものである。すなわち天円の径は 8/5 = 1.6 つまり 1寸6分，地円の径は 12/5 = 2.4 つまり 2寸4分である。

   r1 = 0.8000000;  r2 = 1.2000000;  x = -5.6000000;  y = 3.3000000
   天円径 = 1.6000000,  地円径 = 2.4000000

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, x, y) = res[1]
   r0 = 13//2
   (x1, y1) = (x+r1, y + 3 - r1)
   (x2, y2) = (x + 4 - r2, y + r2)
   @printf("r1 = %.7f;  r2 = %.7f;  x = %.7f;  y = %.7f\n", r1, r2, x, y)
   @printf("天円径 = %.7f,  地円径 = %.7f\n", 2r1, 2r2)
   plot([x, x+4, x+4, x, x], [y, y, y+3, y+3, y], color=:blue, lw=0.5)
   circle(0, 0, r0)
   circle(x1, y1, r1, :green)
   circle(x2, y2, r2, :gold)
   if more == true
       point(x1, y1, "(x1,y1)", :green, :center, :top)
       point(x1, y1, "天円", :green, :center, :bottom)
       point(x2, y2, "(x2,y2)", :gold, :center, :top)
       point(x2, y2, "地円", :gold, :center, :bottom)
       point(x, y, "(x,y)", :blue)
       point(x+4, y+3, "(x+4,y+3)", :blue, :right, :bottom)
       point(0, r0, " r0", :red)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false, xlims=(-6, -0.5), ylims=(3.1, 6.35))
   end
end;

算額（その229）

算額（その229）

京都府京都市上京区 北野天満宮 明治12年(1879)
http://www.wasan.jp/kyoto/kitano2.html

北野天満宮の算額について，永井信一
http://www2.ttcn.ne.jp/~nagai/waseda/wasan/kitano.pdf

藤田貞資：精要算法（下巻），天明元年(1781)
http://www.wasan.jp/seiyou/seiyou.html

二等辺三角形（2つの等辺（上斜）の長さは 1014寸，底辺（下斜）の長さは 1428寸）の中に甲円が 2 個，乙円，丙円が 1 個ずつ入っている。それぞれの径を求めよ。

算額（その110）https://blog.goo.ne.jp/r-de-r/e/f9651e4698b7baef75c28a0647b16424 の愛媛県松山市の伊佐爾波神社の算額では「三角」とあり正三角形であるが，ここでは「圭」なので，二等辺三角形である。

算額（その2031）は甲円の直径のみ求めよとなっている。

甲円の半径，中心座標を r1, (x1, r1)
乙円の半径，中心座標を r2, (0, r3 + r2)
丙円の半径，中心座標を r3, (0, r3)
とおき，以下の方程式を解く。
なお，ピタゴラスの定理から，二等辺三角形の高さは sqrt(1014^2 - 714^2) = 720 である。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms r1::positive, r2::positive, r3::positive, x1::positive;
eq1 = x1^2 + (2r3 + r2 - r1)^2 - (r1 + r2)^2
eq2 = x1^2 + (r1 - r3)^2 - (r1 + r3)^2
eq3 = distance(0, 720, 714, 0, 0, 2r3 + r2) - r2^2  # 上斜への二乗距離
eq4 = distance(0, 720, 714, 0, x1, r1) - r1^2  # 上斜への二乗距離

res = solve([eq1, eq2, eq3, eq4], (r1, r2, r3, x1))

   3-element Vector{NTuple{4, Sym}}:
    (357/2, 15232/75, 2856/25, 1428/5)
    (1447992/1315 + 205632*sqrt(61)/1315, 723996/1315 - 84966*sqrt(61)/1315, -402696/1315 + 102816*sqrt(61)/1315, 17136*sqrt(61)/263 + 308448/263)
    (111384/55 + 34272*sqrt(14)/55, -414596/275 + 113288*sqrt(14)/275, 476/11 + 952*sqrt(14)/11, 2856*sqrt(14)/11 + 17136/11)

2 番めの解が妥当なものである。すなわち甲円，乙円，丙円の直径はそれぞれ 357 寸, 30464/75 寸, 5712/25 寸 である。

   r1 = 178.5000000;  r2 = 203.0933333;  r3 = 114.2400000;  x1 = 285.6000000
   甲円径 = 357.0000000,  乙円径 = 406.1866667;  丙円径 = 228.4800000

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3, x1) = res[1]
   @printf("r1 = %.7f,  r2 = %.7f;  r3 = %.7f;  x1 = %.7f\n", r1, r2, r3, x1)
   @printf("甲円径 = %.7f,  乙円径 = %.7f;  丙円径 = %.7f\n", 2r1, 2r2, 2r3)
   plot([714, 0, -714, 714], [0, 720, 0, 0], color=:blue, lw=0.5)
   circle(0, 2r3 + r2, r2, :green)
   circle(0, r3, r3, :gold)
   circle(x1, r1, r1)
   circle(-x1, r1, r1)
   if more == true
       point(0, 720, " 720", :blue, :left, :bottom)
       point(714, 0, "714", :blue, :left, :bottom)
       point(0, 2r3 + r2, " 2r3+r2", :red)
       point(0, r3, " r3", :red)
       point(x1, r1, "(x1,r1)", :red)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その228）

算額（その228）

冲方丁の「天地明察」中で，金王八幡神社に奉納されたという算額。実際には渋川春海が算額を奉納したという記録はないそうだ。

鉤が 9寸，股が 12寸の鉤股弦に等円を2個図のように入れる。円の径はいくつか。

等円の半径を r とする。
左上の等円の中心座標を (r, y)
右下の等円の中心座標を (x, r)
とおき，以下の方程式を解く。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms r::positive, x::positive, y::positive;

eq1 = (x - r)^2 + (y - r)^2 - 4r^2
eq2 = distance(0, 9, 12, 0, r, y) - r^2  # 弦への二乗距離
eq3 = distance(0, 9, 12, 0, x, r) - r^2  # 弦への二乗距離

res = solve([eq1, eq2, eq3], (r, x, y))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (15/7, 39/7, 33/7)
    (90/17, 234/17, 198/17)

2 番めの解が妥当なものである。すなわち等円の半径は 15/7，直径は 30/7 である。

   r = 2.1428571,  x = 5.5714286;  y = 4.7142857

「天地明察」では，「勾股を掛け合わせ，これを二倍し，勾股弦の総和で割り，弦を掛け，勾股の和で割る」術が述べられている。SymPy では以下のようになる。

using SymPy
@syms 勾, 股
(勾, 股) = (9, 12)
弦 = Int(sqrt(勾^2 + 股^2))
2鉤*股//(鉤 + 股 + 弦)*弦//(鉤 + 股)

30/2

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r, x, y) = res[1]
   @printf("r = %.7f,  x = %.7f;  y = %.7f\n", r, x, y)
   plot([0, 12, 0, 0], [0, 0, 9, 0], color=:blue, lw=0.5)
   circle(r, y, r)
   circle(x, r, r)
   if more == true
       point(0, 9, " 9", :blue, :left, :bottom)
       point(12, 0, " 12", :green, :left, :bottom)
       point(r, y, "(r,y)", :red)
       point(x, r, "(x,r)", :red)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;

算額（その227）

算額（その227）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（217）長野県下高井郡山ノ内町 渋温泉医王殿 慶応元年(1865)

正方形の中に，四分円，大円，中円が各1個，小円が2個入っている。正方形の一辺の長さが与えられたとき，大円，中円，小円の径を求めよ。

円弧を一部とする円の半径，中心座標を r0, (r0, 0)
大円の半径，中心座標を r1，(r0 - r1, r1)
中円の半径，中心座標を r2，(r2, r0 - r2)
小円の半径，中心座標を r3，(r3, y3)
とおき，以下の方程式を r1, r2, r3, y3 について解く（それぞれの解は r0 を含む）。

using SymPy

@syms r0::positive, r1::positive, r2::positive, r3::positive, y3::positive;

eq1 = 2(r0 - r2)^2 - (r0 + r2)^2 |> expand
eq2 = (r0 - r3)^2 + y3^2 - (r0 + r3)^2 |> expand
eq3 = (r2 - r3)^2 + (r0 - r2 - y3)^2 - (r2 + r3)^2 |> expand
eq4 = 2r1^2 - (r0 - r1)^2

res = solve([eq1, eq2, eq3, eq4], (r1, r2, r3, y3))

   3-element Vector{NTuple{4, Sym}}:
    (r0*(-1 + sqrt(2)), r0*(3 - 2*sqrt(2)), r0/2, sqrt(2)*r0)
    (r0*(-1 + sqrt(2)), r0*(3 - 2*sqrt(2)), r0*(3 - 2*sqrt(2))/2, r0*(2 - sqrt(2)))
    (r0*(-1 + sqrt(2)), r0*(2*sqrt(2) + 3), r0*(2*sqrt(2) + 3)/2, r0*(sqrt(2) + 2))

2 番目の解が適切な解である。

r1 = r0*(√2 - 1)
r2 = r0*(3 - 2√2)
r3 = r0*(3 - 2√2)/2 =  r2 / 2
y3 = r0*(2 - √2)

using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(r0, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3, y3) = (r0*(-1 + sqrt(2)), r0*(3 - 2*sqrt(2)), r0*(3 - 2*sqrt(2))/2, r0*(2 - sqrt(2)))
   r1 = r0*(√2 - 1)
   r2 = r0*(3 - 2√2)
   r3 = r0*(3 - 2√2)/2  # =  r2 / 2
   y3 = r0*(2 - √2)
   @printf("r1 = %.7f,  r2 = %.7f;  r3 = %.7f; y3 = %.7f\n", r1, r2, r3, y3)
   println("r3/r2 = $(r3/r2)")
   plot([0, r0, r0, 0, 0], [0, 0, r0, r0, 0], color=:black, lw=0.5)
   circle(r0, 0, r0, beginangle=90, endangle=180)
   circle(r0 - r1, r1, r1, :blue)
   circle(r2, r0 - r2, r2, :green)
   circle(r3, y3, r3, :orange)
   circle(r0 - y3, r0 - r3, r3, :orange)
   if more == true
       point(r0, 0, "r0=$r0 ", :black, :right, :bottom)
       point(r0 - r1, r1, "(r0-r1,r1)", :blue, :center)
       point(r2, r0 - r2, "(r2,r0-r2)", :green, :center)
       point(r3, y3, "(r3,y3)", :orange, :center)
       point(r0 - y3, r0 - r3, "(ro-y3,r0-r3)", :orange, :left, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;