算額（その695）

算額（その695）

神壁算法 關流藤田貞資門人 東都四谷右京殿町 中村幸藏永著 寛政八年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

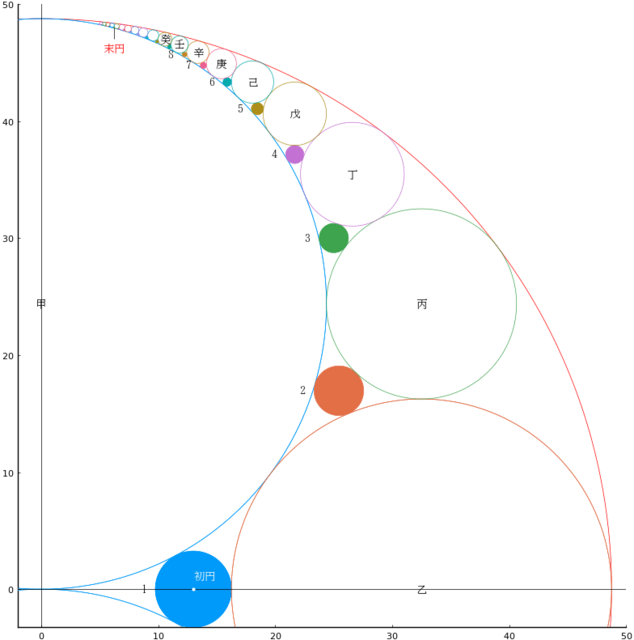
外円内に三斜（不等辺三角形），と 9 個の円が入っている。乙円，丁円，己円の直径がそれぞれ，3 寸，2 寸，1 寸のとき，外円の直径はいかほどか。

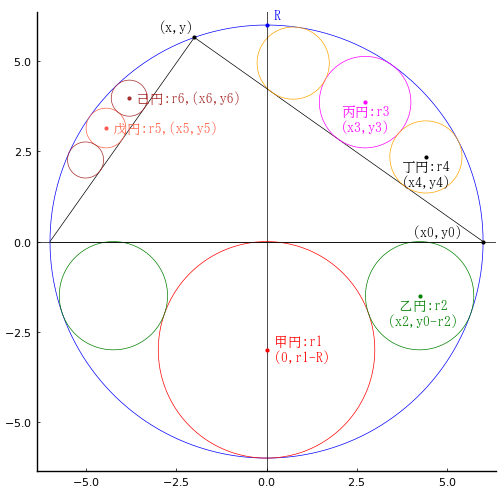
円周上にある三角形の頂点座標を (x0, y0), (x, y); y0 = 2r1 - R, x0 = sqrt(R^2 - y0^2), x = -sqrt(R^2 - y^2)
外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, r1 - R)
乙円の半径と中心座標を r2, (x2, y0 - r2);
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, y4)
戊円の半径と中心座標を r5, (x5, y5)
己円の半径と中心座標を r6, (x6, y6)
とおき，以下の連立方程式を解く。

eq7, eq13 は「算法助術」の公式29 である。

中村信弥編著: 和算の図形公式--『算法助術』--- 
　　http://www.wasan.jp/kosiki/kosiki.html

include("julia-source.txt");

using SymPy
@syms r2, r4, r6, R, x, y, r1, x2, r3, x3, y3, x4, y4, r5, x5, y5, x6, y6

(r2, r4, r6) = (3, 2, 1) .// 2
y0 = 2r1 - R
x0 = sqrt(R^2 - y0^2)
x = -sqrt(R^2 - y^2)
len1 = sqrt((x0 - x)^2 + (y - y0)^2)
len2 = sqrt((x0 + x)^2 + (y - y0)^2)
len3 = sqrt(R^2 - (2r1 - R)^2)

eq1 = x2^2 + (y0- r2)^2 - (R - r2)^2
eq2 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2

eq3 = x3^2 + y3^2 - (R - r3)^2
eq4 = x4^2 + y4^2 - (R - r4)^2
eq5 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2
eq6 = (R - 2r3)^2 + (len1/2)^2 - R^2
eq7 = len1^2 - 4*2R*2r4  # 公式29
eq8 = (2r1 - R - y)/(len3 - x) * y3/x3 + 1

eq9 = x5^2 + y5^2 - (R - r5)^2
eq10 = x6^2 + y6^2 - (R - r6)^2
eq11 = (x5 - x6)^2 + (y5 - y6)^2 - (r5 + r6)^2
eq12 = (R - 2r5)^2 + (len2/2)^2 - R^2
eq13 = len2^2 - 4*2R*2r6  # 公式29
eq14 = (2r1 - R - y)/(len3 + x) * y5/x5 - 1;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (R, y, r1, x2, r3, x3, y3, x4, y4, r5, x5, y5, x6, y6) = u
   return [
       x2^2 - (R - 3/2)^2 + (-R + 2*r1 - 3/2)^2,  # eq1
       x2^2 + (r1 - 3/2)^2 - (r1 + 3/2)^2,  # eq2
       x3^2 + y3^2 - (R - r3)^2,  # eq3
       x4^2 + y4^2 - (R - 1)^2,  # eq4
       -(r3 + 1)^2 + (x3 - x4)^2 + (y3 - y4)^2,  # eq5
       -R^2 + (R - 2*r3)^2 + (sqrt(R^2 - y^2) + sqrt(R^2 - (-R + 2*r1)^2))^2/4 + (R - 2*r1 + y)^2/4,  # eq6
       -16*R + (sqrt(R^2 - y^2) + sqrt(R^2 - (-R + 2*r1)^2))^2 + (R - 2*r1 + y)^2,  # eq7
       1 + y3*(-R + 2*r1 - y)/(x3*(sqrt(R^2 - y^2) + sqrt(R^2 - (-R + 2*r1)^2))),  # eq8
       x5^2 + y5^2 - (R - r5)^2,  # eq9
       x6^2 + y6^2 - (R - 1/2)^2,  # eq10
       -(r5 + 1/2)^2 + (x5 - x6)^2 + (y5 - y6)^2,  # eq11
       -R^2 + (R - 2*r5)^2 + (-sqrt(R^2 - y^2) + sqrt(R^2 - (-R + 2*r1)^2))^2/4 + (R - 2*r1 + y)^2/4,  # eq12
       -8*R + (-sqrt(R^2 - y^2) + sqrt(R^2 - (-R + 2*r1)^2))^2 + (R - 2*r1 + y)^2,  # eq13
       -1 + y5*(-R + 2*r1 - y)/(x5*(-sqrt(R^2 - y^2) + sqrt(R^2 - (-R + 2*r1)^2))),  # eq14
   ]
end;

(r2, r4, r6) = (3, 2, 1) .// 2
iniv = BigFloat[12, 5.5, 3, 4.25, 1.35, 2.75, 3.75, 4.5, 2.2, 0.5, -4.6, 3, -4, 3.8]
res = nls(H, ini=iniv)

   (BigFloat[5.999999999999999999999999999999999999999999999999999999999999999999999999999931, 5.656854249492380195206754896838792314278687501507792292706718951962929913848408, 2.999999999999999999999999999999999999999999999999999999999999999999999999999965, 4.242640687119285146405066172629094235709015626130844219530039213972197435386254, 1.267949192431122706472553658494127633057194746189619371944193020548066983091185, 2.732050807568877293527446341505872366942805253810380628055806979451933016908746, 3.863703305156273146998972798915589470535619356033618201609372305241692855919384, 4.416153642713558008419684820119938656145252405562964502449789354746723815760582, 2.344693370986443557691308802220881143166169766978954662289509621552255928898189, 0.5505102572168219018027159252941086080340525193433298715673074327490396225426752, -4.449489742783178098197284074705891391965947480656670128432692567250960377457299, 3.14626436994197234232913506571557044551247712918732870123248671744266549537083, -3.802437397408490550876329002854725019354381540512873852459501536515540189749589, 3.973848240533267382224213011697627892737753679640435536379640797303909768676809], true)

外円の直径は 12 寸である。

その他のパラメータは以下のとおり。
R = 6;  x = -2;  y = 5.65685;  r1 = 3;  x2 = 4.24264;  r3 = 1.26795;  x3 = 2.73205;  y3 = 3.8637;  x4 = 4.41615;  y4 = 2.34469;  r5 = 0.55051;  x5 = -4.44949;  y5 = 3.14626;  x6 = -3.80244;  y6 = 3.97385

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r4, r6) = (3, 2, 1) .// 2
   (R, x, y, r1, x2, r3, x3, y3, x4, y4, r5, x5, y5, x6, y6) =  [6, -2.4, 5.5, 3, 4.25, 1.35, 2.75, 3.75, 4.5, 2.2, 0.5, -4.6, 3, -4, 3.8]
   (R, y, r1, x2, r3, x3, y3, x4, y4, r5, x5, y5, x6, y6) = res[1]
   x = -sqrt(R^2 - y^2)
   @printf("R = %g;  x = %g;  y = %g;  r1 = %g;  x2 = %g;  r3 = %g;  x3 = %g;  y3 = %g;  x4 = %g;  y4 = %g;  r5 = %g;  x5 = %g;  y5 = %g;  x6 = %g;  y6 = %g\n", R, x, y, r1, x2, r3, x3, y3, x4, y4, r5, x5, y5, x6, y6)
   y0 = 2r1 - R
   x0 = sqrt(R^2 - y0^2)
   plot()
   circle(0, 0, R, :blue)
   segment(-x0, y0, x0, y0)
   segment(x0, y0, x, y)
   segment(-x0, y0, x, y)
   circle(0, r1 - R, r1)
   circle(x2, y0 - r2, r2, :green)
   circle(-x2, y0 - r2, r2, :green)
   circle(x3, y3, r3, :magenta)
   circle(x4, y4, r4, :orange)
   θ1 = 2atand(y3/x3) - atand(y4/x4)
   circle((R - r4)*cosd(θ1), (R - r4)*sind(θ1), r4, :orange)
   circle(x5, y5, r5, :tomato)
   circle(x6, y6, r6, :brown)
   θ2 = 2atand(y5/x5) - atand(y6/x6)
   circle((r6 - R)*cosd(θ2), (r6 - R)*sind(θ2), r6, :brown)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x, y, "(x,y)", :black, :right, :bottom, delta=delta/2)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
       point(x0, y0, "(x0,y0)   ", :black, :right, :bottom, delta=delta/2)
       point(0, r1 - R, " 甲円:r1\n (0,r1-R)", :red, :left, :vcenter)
       point(x2, y0 - r2, " 乙円:r2\n (x2,y0-r2)", :green, :center, delta=-delta/2)
       point(x3, y3, "丙円:r3\n(x3,y3)", :magenta, :center, delta=-delta/2)
       point(x4, y4, "丁円:r4\n(x4,y4)", :black, :center, delta=-delta/2)
       point(x5, y5, " 戊円:r5,(x5,y5)", :tomato, :left, :vcenter)
       point(x6, y6, " 己円:r6,(x6,y6)", :brown, :left, :vcenter)
   end
end;

算額（その694）

算額（その694）

神壁算法 關流藤田貞資門人 久世大和守家士 平井彌五太夫正義 寛政八年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

鈎股弦（直角三角形）内に，斜線，全円，甲円，乙円が入っている。全円，甲円の直径がそれぞれ 19寸7分5厘，3寸1分6厘 のとき，乙円の直径はいかほどか。

直角を挟む2辺（鈎，股）の長さを「鈎」，「股」
斜線と斜辺の交点座標を (x, y)
全円の半径と中心座標を r0, (r0, r0)
甲円の半径と中心座標を r1, (x1, r1)
乙円の半径と中心座標を r2, (r2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r0, r1, 鈎, 股, x1, r2, y2, x, y;

eq1 = 鈎 + 股 - sqrt(鈎^2 + 股^2) - 2r0
eq2 = (r0 - x1)^2 + (r0 - r1)^2 - (r0 + r1)^2
eq3 = (r0 - r2)^2 + (r0 - y2)^2 - (r0 + r2)^2
eq4 = dist(0, 0, x, y, x1, r1) - r1^2
eq5 = dist(0, 0, x, y, r2, y2) - r2^2
eq6 = (鈎 + 股 + sqrt(鈎^2 + 股^2))*r0 - 鈎*股
eq7 = 鈎/股 - y/(股 - x);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (鈎, 股, x1, r2, y2, x, y) = u
   return [
       -2*r0 + 股 + 鈎 - sqrt(股^2 + 鈎^2),  # eq1
       (r0 - r1)^2 - (r0 + r1)^2 + (r0 - x1)^2,  # eq2
       (r0 - r2)^2 - (r0 + r2)^2 + (r0 - y2)^2,  # eq3
       -r1^2 + (r1 - y*(r1*y + x*x1)/(x^2 + y^2))^2 + (-x*(r1*y + x*x1)/(x^2 + y^2) + x1)^2,  # eq4
       -r2^2 + (r2 - x*(r2*x + y*y2)/(x^2 + y^2))^2 + (-y*(r2*x + y*y2)/(x^2 + y^2) + y2)^2,  # eq5
       r0*(股 + 鈎 + sqrt(股^2 + 鈎^2)) - 股*鈎,  # eq6
       -y/(-x + 股) + 鈎/股,  # eq7
   ]
end;

(r0, r1) = (1975, 316) .// 200
iniv = BigFloat[26, 49, 2, 0.6, 5, 5, 24]
res = nls(H, ini=iniv)

   (BigFloat[26.50958690810937781981564610070982992662591012710315095504511369567094160353881, 48.6025397559463070232560931975192400228754697146791710191805408688433795666828, 1.974999999999999999999999999999999999999999999999999999999999999999999999999969, 0.5700002001441297307780475616969606044325776049176168848094355451524229609489859, 5.130001801297167577002428055272645439893198444258551963284919906371806648542264, 5.312669489352098474921664382153576018135850078829535519263800791306165244941906, 23.61186439712043766631850836512700452504822257257571341895022573913851219974303], true)

乙円の直径 = 1.1400004002882596

その他のパラメータは以下のとおり。

鈎 = 26.5096;  股 = 48.6025;  x1 = 1.975;  r2 = 0.57;  y2 = 5.13;  x = 5.31267;  y = 23.6119

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r1) = (1975, 316) .// 200
   (鈎, 股, x1, r2, y2, x, y) = res[1]
   println("乙円の直径 = $(Float64(2r2))")
   @printf("鈎 = %g;  股 = %g;  x1 = %g;  r2 = %g;  y2 = %g;  x = %g;  y = %g\n", 鈎, 股, x1, r2, y2, x, y)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
   circle(r0, r0, r0, :blue)
   circle(x1, r1, r1)
   circle(r2, y2, r2, :green)
   segment(0, 0, x, y, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x, y, " (x,y)", :black, :left, :bottom)
       point(r0, r0, " 全円:r0\n (r0,r0)", :blue, :left, :vcenter)
       point(x1, r1, "  甲円:r1,(x1,r1)", :red, :left, :bottom, delta=delta/2)
       point(r2, y2, " 乙円:r2,(r2,y2)", :green, :left, :vcenter)
       point(股, 0, " 股", :black, :left, :bottom, delta=delta/2)
       point(0, 鈎, " 鈎", :black, :left, :bottom, delta=delta/2)
   end
end;

 

算額（その693）

算額（その693）

神壁算法 關流藤田貞資門人 毛利石見守家士 山邊平助清誠 寛政七年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

算額（その602） に似ている（求めるものが違うが，本質的に同じ）。

外円内に長方形を n 個入れる。それぞれの長方形の長辺の 2 頂点は外円の円周上にあり，残りの 2 頂点は隣の長方形と共有している。
長方形の長辺が 3 寸のとき，外積が最小（n 個の面積の和が最大）になるのは，外円の直径ががいかほどのときか。

外円の半径を R, 内接する長方形の長辺の長さを 2a とする。
長方形の頂点座標 (x, a), (sqrt(R^2 - a^2), a) を求める。
長方形の面積の和は n*(2a * (sqrt(R^2 - a^2) - x)) である。
外積は外円の面積から長方形の面積の和を差し引いたものである。これを B とすれば，B = πR^2 - n*(2a * (sqrt(R^2 - a^2) - x)) となる。

なお，上の図は「神壁算法」にある図に近いように描いたものであるが，これは外円の直径が 13 寸のときのもので，外積は 81.4913891769524 なので，最小値からはかけ離れている。

実際に外積が最小となる場合の図は下の方に示す。

include("julia-source.txt");

using SymPy
@syms n, a, R, B;

x = a/tand(Sym(180)/n)
B = PI*R^2 - n*2a*(sqrt(R^2 - a^2) - x)
B |> println

   pi*R^2 - 2*a*n*(-a/tan(pi/n) + sqrt(R^2 - a^2))

たとえば，問のように n = 10, a = 3/2 の場合には，以下の B2 のようになる。

B2 = B(n => 10, a => 3//2)
B2 |> println

   pi*R^2 - 30*sqrt(R^2 - 9/4) + 45/sqrt(1 - 2*sqrt(5)/5)

B2 の値は R により変化するが，R = 5 近辺で最小値を取ることがわかる。

using Plots
pyplot(size=(300, 150), grid=false, aspectratio=:none, label="")
plot(B2, xlims=(0,10), xlabel="外円の半径", ylabel="黒積")

B が最小値となるのは，B の導関数が 0 になるときである。

まず，導関数 g を求める。

g = diff(B, R)
g |> println

   -2*R*a*n/sqrt(R^2 - a^2) + 2*pi*R

導関数 = 0 となる R を求めるために solve() を用いる。

3 組の解が得られるが，3 番目のものが適解である。

R0 = solve(g, R)
R0 |> println
R0[3] |> println

   Sym[0, -a*sqrt(n^2 + pi^2)/pi, a*sqrt(n^2 + pi^2)/pi]
   a*sqrt(n^2 + pi^2)/pi

a, n に具体的な値を代入すれば，黒積が最小になるときの外円の半径が得られる。

R0[3](a=>3/2, n => 10).evalf() |> println

   5.00472439995710

外円の半径が与えられると黒積が得られる。

B(R => R0[3]) |> println

   a^2*(n^2 + pi^2)/pi - 2*a*n*(-a/tan(pi/n) + sqrt(a^2*(n^2 + pi^2)/pi^2 - a^2))

a, n に具体的な値を代入すれば，黒積が最小のときの値が得られる。

B(R => R0[3], a=>3/2, n => 10).evalf() |> println

   73.9446182521105

長辺の長さが 3 の 10 個の長方形を入れるとき，外円の直径が 10.0094 のときに黒積が最小値 73.9446 をとる。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (n, a) = (10, 3//2)  # 条件として与えられる
   x = a/tand(Sym(180)/n)
   R = a*sqrt(n^2 + pi^2)/pi
   B = a^2*(n^2 + pi^2)/pi - 2*a*n*(-a/tan(pi/n) + sqrt(a^2*(n^2 + pi^2)/pi^2 - a^2))
   B0 = pi*R^2 - n*2a*(sqrt(R^2 - a^2) - x)
   @printf("長辺の長さが %g の %i 個の長方形を入れるとき，外円の直径が %g のときに黒積が最小値 %g をとる\n", 2a, n, 2R, B)
   plot()
   circle(0, 0, R, :blue)
   XY = [x sqrt(R^2 - a^2) sqrt(R^2 - a^2) x x;
           -a -a a a -a]
   for deg in 0:360/n:359
       XY2 = [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * XY
       plot!(XY2[1, :], XY2[2, :])
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
       point(x, a, "(x,a) ", :black, :right, :top)
       point(√(R^2-a^2), a, "(√(R^2-a^2),a) ", :black, :right, :bottom, delta=delta)
   end
end;

算額（その692）

算額（その692）

神壁算法 關流藤田貞資門人 龜井隠岐守家士 堀田人助泉尹 天明八年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

直径 97 寸 5 分の大円の中に累円と，大円と甲円と累円に挟まれる円がある。
末円の直径が 1 分のとき，初円から末円まで何個の挟円があるか（つまり，末円は初円から数えて何番目か）。

大円の半径と中心座標を r0, (0, 0)
甲円の半径と中心座標を r1, (x1, y1); x1 = 0, y1 = r1
乙円の半径と中心座標を r2, (x2, y2); x2 = r0 - r2, y2 = 0
乙円以降 i 番目の円の半径と中心座標を ri, (xi, yi)
初円の半径と中心座標を R1, X1, Y1
初円以降 i 番目の挟円の半径と中心座標を Ri, (Xi, Yi)
とおき，順次パラメータを決定していく。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r0::positive, r1::positive,
     r2::positive, x2::positive, y2::real,
     r3::positive, x3::positive, y3::positive;

まず，乙円については，半径 r2 = r0/3 になる。

r1 = r0/2
x2 = r0 - r2
y2 = 0
eq1 = x2^2 + r1^2 - (r1 + r2)^2
res2 = solve(eq1, r2)
res2[1] |> println

   r0/3

次に，丙円については，半径，中心座標は (r0/6, 2*r0/3, r0/2) になる。

r2 = r0/3
x2 = r0 - r2
y2 = 0
eq2 = x3^2 + y3^2 - (r0 - r3)^2
eq3 = x3^2 + (r1 - y3)^2 - (r1 + r3)^2
eq4 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
res3 = solve([eq2, eq3, eq4], (r3, x3, y3))

   1-element Vector{Tuple{Sym, Sym, Sym}}:
    (r0/6, 2*r0/3, r0/2)

更に，丁円については，半径，中心座標は (r0/11, 6*r0/11, 8*r0/11) になる。

@syms r4, x4, y4
(r3, x3, y3) = res3[1]
eq5 = x4^2 + y4^2 - (r0 - r4)^2
eq6 = x4^2 + (r1 - y4)^2 - (r1 + r4)^2
eq7 = (x3 - x4)^2 + (y3 - y4)^2 - (r3 + r4)^2
res4 = solve([eq5, eq6, eq7], (r4, x4, y4))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r0/11, 6*r0/11, 8*r0/11)
    (r0/3, 2*r0/3, 0)

@syms r5, x5, y5
(r4, x4, y4) = res4[1]
eq8 = x5^2 + y5^2 - (r0 - r5)^2
eq9 = x5^2 + (r1 - y5)^2 - (r1 + r5)^2
eq10 = (x4 - x5)^2 + (y4 - y5)^2 - (r4 + r5)^2
res5 = solve([eq8, eq9, eq10], (r5, x5, y5))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r0/18, 4*r0/9, 5*r0/6)
    (r0/6, 2*r0/3, r0/2)

@syms r6, x6, y6
(r5, x5, y5) = res5[1]
eq11 = x6^2 + y6^2 - (r0 - r6)^2
eq12 = x6^2 + (r1 - y6)^2 - (r1 + r6)^2
eq13 = (x5 - x6)^2 + (y5 - y6)^2 - (r5 + r6)^2
res6 = solve([eq11, eq12, eq13], (r6, x6, y6))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r0/27, 10*r0/27, 8*r0/9)
    (r0/11, 6*r0/11, 8*r0/11)

@syms r7, x7, y7
(r6, x6, y6) = res6[1]
eq14 = x7^2 + y7^2 - (r0 - r7)^2
eq15 = x7^2 + (r1 - y7)^2 - (r1 + r7)^2
eq16 = (x6 - x7)^2 + (y6 - y7)^2 - (r6 + r7)^2
res7= solve([eq14, eq15, eq16], (r7, x7, y7))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r0/38, 6*r0/19, 35*r0/38)
    (r0/18, 4*r0/9, 5*r0/6)

@syms r8, x8, y8
(r7, x7, y7) = res7[1]
eq17 = x8^2 + y8^2 - (r0 - r8)^2
eq18 = x8^2 + (r1 - y8)^2 - (r1 + r8)^2
eq19 = (x7 - x8)^2 + (y7 - y8)^2 - (r7 + r8)^2
res8= solve([eq17, eq18, eq19], (r8, x8, y8))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r0/51, 14*r0/51, 16*r0/17)
    (r0/27, 10*r0/27, 8*r0/9)

累円のパラメータ，半径，中心座標を表す数列には規則性があり，以下のような一般項になる。
甲円の半径 r1，中心座標 (x1, y1) は r0/2, (0, r1)
乙円の半径 r2，中心座標 (x2, y2) は r0/3, (r0 - r2, 0)
丙円以降は i ≧ 3 として，ri, (xi, yi) は以下のようになる。
ri = r0/(i^2 - 2i + 3)
xi = ri*(2i - 2)
yi = ri*(i^2 - 2i)

次に，互いに接する，外円と 2 個の累円に挟まれる円のパラメータを計算する。

@syms R1, X1
X1 = r0 - 2r2 - R1
eq20 = X1^2 + r1^2 - (r1 + R1)^2
res11 = solve(eq20, R1)
res11[1] |> println

   r0/15

R1 = r0/15
X1 = r0 - 2r2 - R1
(R1, X1)

   (r0/15, 4*r0/15)

@syms R2, X2, Y2
(x1, y1, x2, y2) = (0, r1, r0 - r2, 0)
(R1, X1) = (r0/15, 4*r0/15)
eq21 =  X2^2       + (Y2 - y1)^2 - (R2 + r1)^2
eq22 = (X2 - x2)^2 + (Y2 - y2)^2 - (R2 + r2)^2
eq23 = (X2 - x3)^2 + (Y2 - y3)^2 - (R2 + r3)^2
res12 = solve([eq21, eq22, eq23], (R2, X2, Y2))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (-r0, 0, 0)
    (r0/23, 12*r0/23, 8*r0/23)

@syms R3, X3, Y3
(R2, X2, Y2) = res12[2]
eq24 =  X3^2       + (Y3 - y1)^2 - (R3 + r1)^2
eq25 = (X3 - x3)^2 + (Y3 - y3)^2 - (R3 + r3)^2
eq26 = (X3 - x4)^2 + (Y3 - y4)^2 - (R3 + r4)^2
res13 = solve([eq24, eq25, eq26], (R3, X3, Y3))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (-r0, 0, 0)
    (r0/39, 20*r0/39, 8*r0/13)

@syms R4, X4, Y4
#(x1, y1, x2, y2) = (0, r1, r0 - r2, 0)
(R3, X3, Y3) = res13[2]
eq27 =  X4^2       + (Y4 - y1)^2 - (R4 + r1)^2
eq28 = (X4 - x4)^2 + (Y4 - y4)^2 - (R4 + r4)^2
eq29 = (X4 - x5)^2 + (Y4 - y5)^2 - (R4 + r5)^2
res14 = solve([eq27, eq28, eq29], (R4, X4, Y4))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (-r0, 0, 0)
    (r0/63, 4*r0/9, 16*r0/21)

@syms R5, X5, Y5
#(x1, y1, x2, y2) = (0, r1, r0 - r2, 0)
(R4, X4, Y4) = res14[2]
eq30 =  X5^2       + (Y5 - y1)^2 - (R5 + r1)^2
eq31 = (X5 - x5)^2 + (Y5 - y5)^2 - (R5 + r5)^2
eq32 = (X5 - x6)^2 + (Y5 - y6)^2 - (R5 + r6)^2
res14 = solve([eq30, eq31, eq32], (R5, X5, Y5))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (-r0, 0, 0)
    (r0/95, 36*r0/95, 16*r0/19)

挟円のパラメータは
初円は
R1 = r0/15, X1 = 4*r0/15, Y1 = 0
二円以降 i ≧ 2 においては
半径 Ri = r0/(4i^2 - 4i + 15)
x座標 Xi = Ri * (8i - 4)
y座標 Yi = Ri * (4i^2 - 4i)

問は，「末円の径が一分であるとき，それは何番目の挟円か」ということである。
以下の方程式を解けば，16番目の挟円であることがわかる。

@syms i::positive
r0 = 975/20  # 直径 = 97.5
eq = r0/(4i^2 - 4i + 15) - 1//20  # 直径 = 0.1 寸
solve(eq, i)[1] |> println

   16.0000000000000

一般的な解を求めるには，末円の半径を Rn とすれば

@syms i::positive, r0::positive, Rn::positive
eq = r0/(4i^2 - 4i + 15) - Rn
res = solve(eq, i)[2]
res |> println

   1/2 + sqrt(-14*Rn + r0)/(2*sqrt(Rn))

SymPy ではこれ以上簡単にできないが，手計算で，(1 + sqrt(r0/Rn - 14))/2 となる。

「外円の半径を末円の半径で割り，14を引いて，開平し，1を加えて，2で割る」となり，「術」と一致する。
なお，当たり前であるが，術は，半径を直径と読み替えても成り立つ。

ちなみに，20番目の挟円の半径は 0.031759 ほどであり，数値を丸めるとたしかに20番目である事がわかる。

(sqrt(97.5/(2*0.031759) - 14) + 1)/2

   19.99998688035496

それぞれの円のパラメータは以下通り。

   番号:   累円 xi,   累円 yi,   累円 ri;    挟円 Xi,   挟円 Yi,    挟円Ri
      1:  0.000000, 24.375000, 24.375000;  13.000000,  0.000000,  3.250000
      2: 32.500000,  0.000000, 16.250000;  25.434783, 16.956522,  2.119565
      3: 32.500000, 24.375000,  8.125000;  25.000000, 30.000000,  1.250000
      4: 26.590909, 35.454545,  4.431818;  21.666667, 37.142857,  0.773810
      5: 21.666667, 40.625000,  2.708333;  18.473684, 41.052632,  0.513158
      6: 18.055556, 43.333333,  1.805556;  15.888889, 43.333333,  0.361111
      7: 15.394737, 44.901316,  1.282895;  13.852459, 44.754098,  0.266393
      8: 13.382353, 45.882353,  0.955882;  12.238494, 45.690377,  0.203975
      9: 11.818182, 46.534091,  0.738636;  10.940594, 46.336634,  0.160891
     10: 10.572289, 46.987952,  0.587349;   9.880000, 46.800000,  0.130000
     11:  9.558824, 47.316176,  0.477941;   9.000000, 47.142857,  0.107143
     12:  8.719512, 47.560976,  0.396341;   8.259669, 47.403315,  0.089779
     13:  8.013699, 47.748288,  0.333904;   7.629108, 47.605634,  0.076291
     14:  7.412281, 47.894737,  0.285088;   7.086137, 47.765814,  0.065612
     15:  6.893939, 48.011364,  0.246212;   6.614035, 47.894737,  0.057018
     16:  6.442731, 48.105727,  0.214758;   6.200000, 48.000000,  0.050000
     17:  6.046512, 48.183140,  0.188953;   5.834089, 48.087035,  0.044198
     18:  5.695876, 48.247423,  0.167526;   5.508475, 48.159806,  0.039346
     19:  5.383436, 48.301380,  0.149540;   5.216920, 48.221258,  0.035249
     20:  5.103306, 48.347107,  0.134298;   4.954397, 48.273616,  0.031759

function circle4f(x, y, r, color=:red)
  circlef(x, y, r, color)
  circlef(x, -y, r, color)
  circlef(-x, y, r, color)
  circlef(-x, -y, r, color)
end;

function draw(more=false)
   pyplot(size=(800, 800), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   n = 20
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   r = Vector{Float64}(undef, n)
   x = Vector{Float64}(undef, n)
   y = Vector{Float64}(undef, n)
   r0 = 975//20
   r1 = r0/2
   r2 = r0/3
   x2 = r0 - r2
   (r[1], x[1], y[1]) = (r1, 0, r1)
   (r[2], x[2], y[2]) = (r2, x2, 0)
   for i in 3:n
       factor = r0/(i^2 - 2i + 3)
       r[i] = factor
       x[i] = factor*(2i - 2)
       y[i] = factor*(i^2 - 2i)
   end
   R = Vector{Float64}(undef, n)
   X = Vector{Float64}(undef, n)
   Y = Vector{Float64}(undef, n)
   (R[1], X[1], Y[1]) = (r0/15, 4*r0/15, 0)
   for i in 2:n
       factor = r0/(4i^2 - 4i + 15)
       R[i] = factor
       X[i] = factor*(8i - 4)
       Y[i] = factor*(4i^2 - 4i)
   end
   plot()
   circle(0, 0, r0)
   @printf("%4s: %9s, %9s, %9s;  %9s, %9s, %9s\n", "番号", "累円 xi", "累円 yi", "累円 ri", "挟円 Xi", "挟円 Yi", "挟円Ri")
   for i in 1:n
       @printf("%4i: %9.6f, %9.6f, %9.6f;  %9.6f, %9.6f, %9.6f\n", i, x[i], y[i], r[i], X[i], Y[i], R[i])
       circle4(x[i], y[i], r[i], i)
       circle4f(X[i], Y[i], R[i], i)
       i < 11 && point(x[i], y[i], names[i], :black, :center, :vcenter, mark=false)
       i < 9 && point(X[i]-R[i]-1, Y[i], string(i), :black, :center, :vcenter, mark=false)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(X[1], Y[1], "初円", :white, :left, :bottom, delta=delta/2)
       segment(X[16], Y[16], X[16], Y[16] - 1)
       point(X[16], Y[16] - 1, "末円", :red, :center, :top, delta=-delta/4, mark=false)
       plot!(xlims=(-2, 50), ylims=(-R[1], 50))
   end
end;

 

算額（その691）

算額（その691）

神壁算法 東都本郷春木町一丁目 佐野富次郎安行 天明七年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

楕円の中に大円 2 個，中円 2 個，小円 1 個が入っている。
楕円の長径，短径がそれぞれ 2168 寸，1084 寸のとき，大円の直径はいかほどか。

楕円の長半径と短半径を a, b
大円の半径と中心座標を r1, (x1, 0); x1 = r1 + r3
中円の半径と中心座標を r2, (0, b - r2)
小円の半径と中心座標を r3, (0, 0)
楕円と大円の共通接点の座標を (x0, y0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a::positive, b::positive, x0::positive, y0::positive,
     r1::positive, x1::positive,r2::positive, r3::positive
(a, b) = (2168, 1084) .// 2
x1 = r1 + r3
eq1 = (x0 - x1)^2 + y0^2 - r1^2
eq2 = -b^2*x0/(a^2*y0) - (x1 - x0)/y0
eq3 = x0^2/a^2 + y0^2/b^2 - 1
eq4 = r3 + 2r2 - b
eq5 = x1^2 + (b - r2)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3, eq4, eq5], (x0, y0, r1, r2, r3))

   1-element Vector{NTuple{5, Sym}}:
    (-1626/7 + 2710*sqrt(57)/21, sqrt(6315926/147 + 734410*sqrt(57)/49), 271*sqrt(57)/14 + 4065/14, 3523/7 - 271*sqrt(57)/7, -3252/7 + 542*sqrt(57)/7)

大円の直径は (271√57 + 4065)/7 = 873.000733136910 寸である。
ちなみに，中円，小円の直径はそれぞれ 421.998533726179 寸，240.002932547642 寸である。

res[1][3].evalf()*2 |> println
res[1][4].evalf()*2 |> println
res[1][5].evalf()*2 |> println

   873.000733136910
   421.998533726179
   240.002932547642

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (2168, 1084) .// 2
   (x0, y0, r1, r2, r3) = (-1626/7 + 2710*sqrt(57)/21, sqrt(6315926/147 + 734410*sqrt(57)/49), 271*sqrt(57)/14 + 4065/14, 3523/7 - 271*sqrt(57)/7, -3252/7 + 542*sqrt(57)/7)
   x1 = r1 + r3
   plot()
   ellipse(0, 0, a, b, color=:orange)
   circle(x1, 0, r1)
   circle(-x1, 0, r1)
   circle(0, 0, r3, :green)
   circle(0, b - r2, r2, :blue)
   circle(0, r2 - b, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(a, 0, " a", :black, :left, :bottom, delta=delta)
       point(0, b, " b", :black, :left, :bottom, delta=delta)
       point(x0, y0, "(x0,y0)", :red, :left, :bottom, delta=delta)
       point(x1, 0, "大円:r1,(x1,y1)", :red, :center, delta=-delta)
       point(0, b - r2, " 中円:r2,(0,b-r2)", :black, :left, :vcenter)
       point(0, r3, " r3", :black, :left, :bottom, delta=delta)
       point(0, r3, " 小円", :black, :left, :top, delta=-delta)
   end
end;

 

算額（その690）

算額（その690）

神壁算法 一柳土佐守家士 高瀬恆右衛門信之 寛政八年
藤田貞資(1789)：神壁算法巻上
http://www.wasan.jp/jinpeki/jinpekisanpo1.pdf

外円の中に大円 5 個，小円 10 個が入っている。外円の直径が 33 寸 99 分のとき，小円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
小円の半径と中心座標を r2, (x1, y1), (x2, y2)
とおき，以下の連立方程式を解く。

単なる二元連立方程式であるが，SymPy の性能では，解析解を求めることができない。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms R::positive, r1::positive, r2::positive,
     x1::positive, y1::positive, x2::positive, y2::positive

R = 33.99/2
x1 = (R - r2)*cosd(54)
y1 = (R - r2)*sind(54)
x2 = (R - r1)*cosd(36)*cosd(54)
y2 = (R - r1)*cosd(36)*sind(54)
eq1 = x1^2 + (R - r1 - y1)^2 - (r1 + r2)^2
eq2 = x2^2 + (R - r1 - y2)^2 - (r1 - r2)^2
res = solve([eq1, eq2], (r1, r2))

   2-element Vector{Tuple{Sym, Sym}}:
    (0.972560942096724, 10.3903143260872)
    (7.45655928660198, 1.85000450540052)

2 番目の解が適解である。

小円の直径は 2\*1.85000450540052 = 3.70000901080104
大円の直径は 2\*7.45655928660198 = 14.91311857320396

その他のパラメータは以下の通りである。

   R = 16.995;  r1 = 7.45656;  r2 = 1.85;  x1 = 8.902;  y1 = 12.2526;  x2 = 4.5358;  y2 = 6.24299

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 33.99/2
   (r1, r2) = (7.45655928660198, 1.85000450540052)
   x1 = (R - r2)*cosd(54)
   y1 = (R - r2)*sind(54)
   x2 = (R - r1)*cosd(36)*cosd(54)
   y2 = (R - r1)*cosd(36)*sind(54)
   @printf("小円の直径 = %g\n", 2r2)
   @printf("R = %g;  r1 = %g;  r2 = %g;  x1 = %g;  y1 = %g;  x2 = %g;  y2 = %g\n",
       R, r1, r2, x1, y1, x2, y2)
   plot()
   circle(0, 0, R, :orange)
   rotate(0, R - r1, r1, angle=72)
   rotate(x1, y1, r2, :blue, angle=72)
   rotate(x2, y2, r2, :blue, angle=72)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, R - r1, " 大円:r1\n (0,R-r1)", :red, :left, :bottom, delta=delta)
       point(x1, y1, " 小円:r2,(x1,y1)", :black, :left, :vcenter)
       point(x2, y2, " 小円:r2,(x2,y2)", :black, :left, :vcenter)
   end
end;

 

算額（その689）

算額（その689）

和算問題あれこれ 2 令和5年4月の問題-No.2（『神壁算法』15問）
https://gunmawasan.web.fc2.com/k-n-mondai.html

大円内に等脚台形と小円をいれる。台形の上底（上頭），下底（下頭），対角線（内斜）がそれぞれ 36 寸，300 寸，280 寸のとき，小円の直径は何寸か。
注：「神壁算法」の図の寸法を10倍している。

 

大円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r0, (x0, y0)
上底，下底と円の交点座標を (x1, y1), (x2, y2)
とおき，以下の連立方程式を解く。

なお，4 元連立方程式として一度に解くことはできるが，R, r0 が負の値になる（絶対値を取ればもんだいはない）ので，eq1, eq2 の 2 元連立方程式として R, r0 を求め，ついで eq3, eq4 で x0，y0 を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms R::positive, x1::positive, y1::positive, x2::positive, y2::negative, r0::positive, x0::positive, y0::positive

(x1, x2) = (300, 36) .// 2
y1 = -sqrt(R^2 - x1^2)
y2 = sqrt(R^2 - x2^2)
eq1 = (x1 + x2)^2 + (y2 - y1)^2 - 280^2
eq2 = 2sqrt(R^2 - (R - 2r0)^2) - sqrt((x1 - x2)^2 + (y2 - y1)^2);
solve([eq1, eq2], (R, r0))

   2-element Vector{Tuple{Sym, Sym}}:
    (325/2, 65/2)
    (325/2, 130)

最初のものが適解である。

小円の直径は 65 寸である。ちなみに，外円の直径は 325 寸である。

図を描くために，小円の中心座標 (x0, y0) を求める。

(R, r0) = (325//2, 65//2)
eq3 = x0^2 + y0^2 - (R - r0)^2
eq4 = y0/x0 * (sqrt(R^2 - x2^2) + sqrt(R^2 - x1^2))/(x2 - x1) + 1;
solve([eq3, eq4], (x0, y0))

   1-element Vector{Tuple{Sym, Sym}}:
    (112.000000000000, 66.0000000000000)

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (x1, x2) = (300, 36) .// 2
   (R, r0, x0, y0) = [325/2, 65/2, 112, 66]
   y1 = -sqrt(R^2 - x1^2)
   y2 = sqrt(R^2 - x2^2)
   @printf("小円の直径 = %g\n", 2r0)
   @printf("R = %g;  x0 = %g;  y0 = %g;  r0 = %g\n", R, x0, y0, r0)
   plot([x1, x2, -x2, -x1, x1], [y1, y2, y2, y1, y1], color=:black, lw=0.5)
   circle(0, 0, R)
   circle(x0, y0, r0, :blue)
   segment(-x2, y2, x1, y1, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x0, y0, "小円:r0\n(x0,y0)", :blue, :center, delta=-delta/2)
       point(R, 0, " R", :red, :left, :bottom, delta=delta)
       point(x1, y1, "(x1,y1)")
       point(x2, y2, "(x2,y2)", :green, :left, :bottom, delta=delta)
   end
end;

 

算額（その688）

算額（その688）

和算問題あれこれ 2 令和5年10月の問題-No.3（『五明算法』34問）
https://gunmawasan.web.fc2.com/k-n-mondai.html

扇面に 6 この円が入っている，甲円，乙円の直径が 1.75 寸，2.25 寸のとき，丁円の直径はいかほどか。

扇の長さ（半径）と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, y3); r3 = r1 + r4
丁円の半径と中心座標を r4, (0, R - 2r1 - r4)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms R, r1, r2, x2::positive, y2, r3, x3, y3, r4, x0, y0
(r1, r2) = (175, 225) .// 200
r3 = r1 + r4
eq1 = x2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
eq2 = (x3 - x2)^2 + (y3 - y2)^2 - (r3 + r2)^2
eq3 = x3^2 + (R -2r1 - r4 - y3)^2 - (r3 + r4)^2
eq4 = x3^2 + y3^2 - (R - r3)^2
eq5 = x2^2 + (y2 -R + 2r1 + r4)^2 - (r2 + r4)^2
eq6 = x2^2 + y2^2 - (R - r2)^2
res1 = solve([eq1, eq2, eq3, eq4, eq5, eq6], (R, x2, y2, x3, y3, r4))

   1-element Vector{NTuple{6, Sym}}:
    (63/8, 9*sqrt(47)/32, 207/32, 189*sqrt(47)/320, 5607/1600, 329/200)

丁円の直径は 329/100 = 3.29 寸である。

その他のパラメータは以下の通りである。

   r1 = 0.875;  r2 = 1.125;  R = 7.875;  x2 = 1.92815;  y2 = 6.46875;  x3 = 4.04912;  y3 = 3.50438;  r4 = 1.645;  x0 = 7.67922;  y0 = 1.74504

問の答えはここまででよいが，図を描くために追加の計算をする。
扇の角の座標 (x0, y0) を求める。

@syms R, r1, r2, x2::positive, y2, r3, x3, y3, r4, x0::positive, y0::positive
(r1, r2) = (175, 225) .// 200
(R, x2, y2, x3, y3, r4) = res1[1]
r3 = r1 + r4
eq11 = x0^2 + y0^2 - R^2
eq12 = distance(0, 0, x0, y0, x3, y3) - r3^2
res2 = solve([eq11, eq12], (x0, y0))

   2-element Vector{Tuple{Sym, Sym}}:
    (-5607/2312 + 14175*sqrt(47)/18496, 945*sqrt(47)/2312 + 84105/18496)
    (5607/2312 + 14175*sqrt(47)/18496, 84105/18496 - 945*sqrt(47)/2312)

2 組の解が得られるが，2 番目のものが適解である。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (175, 225) .// 200
   (R, x2, y2, x3, y3, r4) = (63/8, 9*sqrt(47)/32, 207/32, 189*sqrt(47)/320, 5607/1600, 329/200)
   r3 = r1 + r4
   (x0, y0) = (5607/2312 + 14175*sqrt(47)/18496, 84105/18496 - 945*sqrt(47)/2312)
   θ = atand(y0/x0)
   println("丁円の直径 = $(2r4)")
   @printf("r1 = %g;  r2 = %g;  R = %g;  x2 = %g;  y2 = %g;  x3 = %g;  y3 = %g;  r4 = %g;  x0 = %g;  y0 = %g\n", r1, r2, R, x2, y2, x3, y3, r4, x0, y0)
   plot()
   circle(0, 0, R, beginangle=θ, endangle=180-θ, n=1500)
   circle(0, 0, R - 2r3, :orange, beginangle=θ, endangle=180-θ, n=1500)
   segment(0, 0, x0, y0)
   segment(0, 0, -x0, y0)
   circle(0, R - r1, r1, :blue)
   circle(x2, y2, r2, :magenta)
   circle(-x2, y2, r2, :magenta)
   circle(x3, y3, r3, :green)
   circle(-x3, y3, r3, :green)
   circle(0, R - 2r1 - r4, r4, :tomato)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, R - r1, " 甲円:r1,(0,R-r1)", :black, :left, :vcenter)
       point(x2, y2, " 乙円:r2,(x2,y2)", :black, :left, :vcenter)
       point(x3, y3, " 丙円:r3\n (x3,y3)", :green, :left, :vcenter)
       point(0, R-2r1-r4, " 丁円:r4\n (0,R-2r1-r4)", :black, :left, :vcenter)
       point(0, R, " R", :black, :left, :bottom, delta=delta)
       point(0, R - 2r3, " R-2r3", :black, :left, delta=-delta)
       point(x0, y0, "(x0,y0) ", :red, :right, :bottom, delta=delta/2)
   end
end;

算額（その687）

算額（その687）

和算問題あれこれ 2 令和5年7月の問題-No.2（『神壁算法』第53問）
https://gunmawasan.web.fc2.com/k-n-mondai.html

台形内に左斜と右斜の2本の線分を設ける。左斜，右斜，闊（高さ）の長さがそれぞれ 15 寸，5 寸，12 寸である。甲，乙を変化させたとき，台形の面積が最大になるときの甲，乙の長さを求めよ。

横倒しになっている台形であるが，下底（左側），下底（右側）の長さはそれぞれ固定されているので，甲によって増減する。したがって，上底，下底，闊により決まる面積も甲の関数になる。
面積(甲) = 闊*(sqrt(右斜^2 - 甲^2) + sqrt(左斜^2 - (-甲 + 闊)^2))/2
左斜，右斜，闊 がそれぞれ 15, 5, 12 ならば
面積(甲) = 6*sqrt(25 - 甲^2) + 6*sqrt(225 - (12 - 甲)^2)
である。甲を横軸，面積を縦軸に取り図を描いてみる。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms 甲, 左斜, 右斜, 闊, 下底, 上底, 面積
(左斜, 右斜, 闊) = ( 15, 5, 12)
下底 = sqrt(左斜^2 -  (闊 - 甲)^2)
上底 = sqrt(右斜^2 -  甲^2)
面積 = (下底 + 上底)*闊/2
面積 |> println

   6*sqrt(25 - 甲^2) + 6*sqrt(225 - (12 - 甲)^2)

pyplot(size=(300, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(面積, xlims=(0, 5), xlabel="甲", ylabel="面積")

図より，甲が3前後のときに面積が最大になることがわかる。

面積が最大になるときの甲は，面積の導関数を求めそれが 0 になるときの値である。方程式を解くことにより，甲 = 3 である。また，このとき面積を表す関数の甲にその値を代入すれば，最大値が 96 であることがわかる。

solve(diff(面積))[1] |> println

   3

面積(甲 => 3) |> println

   96

 

 

算額（その686）

算額（その686）

三七 児玉郡上里村勅使河原 丹生神社 弘化3年(1846)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

和算問題あれこれ 2 令和5年11月の問題-No.2（『神壁算法』第34問）
https://gunmawasan.web.fc2.com/k-n-mondai.html

長方形内に斜線を2本入れ，区分された領域に内接円を 4 個入れる。亨円，貞円の直径がそれぞれ 44 寸，33 寸のとき，利円の直径はいかほどか。

長方形の左下頂点を原点とし，長辺の長さを a とする（短辺の長さは元円の直径 2r1）
斜線と長辺の交点座標を (c, 0 ), (b, 0), (d, 2r1)
元円の半径と中心座標を r1, (a - r1, r1)
亨円の半径と中心座標を r2, (x2, 2r1 - r2)
利円の半径と中心座標を r3, (r3, r3)
貞円の半径と中心座標を r4, (x4, r4)
とおき，以下の連立方程式を解く。
eq1〜eq7 は円の中心から斜線への距離に関する方程式，eq8 は元円と亨円の半径の相似比についての方程式である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms a, b, c, d, r1, r2, x2, r3, r4, x4

#(r2, r4) = (44, 33).//2

eq1 = dist(c, 0, d, 2r1, a - r1, r1) - r1^2
eq2 = dist(c, 0, d, 2r1, x2, 2r1 - r2) - r2^2
eq3 = dist(c, 0, d, 2r1, r3, r3) - r3^2
eq4 = dist(c, 0, d, 2r1, x4, r4) - r4^2
eq5 = dist(b, 0, 0, 2r1, x2, 2r1 - r2) - r2^2
eq6 = dist(b, 0, 0, 2r1, r3, r3) - r3^2
eq7 = dist(b, 0, 0, 2r1, x4, r4) - r4^2
eq8 = r2/x2 - r1/(a - r1);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (a, b, c, d, r1, x2, r3, x4) = u
   return [
       -r1^2 + (-2*r1*(2*r1^2 + (-c + d)*(a - c - r1))/(4*r1^2 + (-c + d)^2) + r1)^2 + (a - c - r1 - (-c + d)*(2*r1^2 + (-c + d)*(a - c - r1))/(4*r1^2 + (-c + d)^2))^2,  # eq1
       -r2^2 + (-c + x2 - (-c + d)*(2*r1*(2*r1 - r2) + (-c + d)*(-c + x2))/(4*r1^2 + (-c + d)^2))^2 + (2*r1 - 2*r1*(2*r1*(2*r1 - r2) + (-c + d)*(-c + x2))/(4*r1^2 + (-c + d)^2) - r2)^2,  # eq2
       -r3^2 + (-2*r1*(2*r1*r3 + (-c + d)*(-c + r3))/(4*r1^2 + (-c + d)^2) + r3)^2 + (-c + r3 - (-c + d)*(2*r1*r3 + (-c + d)*(-c + r3))/(4*r1^2 + (-c + d)^2))^2,  # eq3
       -r4^2 + (-2*r1*(2*r1*r4 + (-c + d)*(-c + x4))/(4*r1^2 + (-c + d)^2) + r4)^2 + (-c + x4 - (-c + d)*(2*r1*r4 + (-c + d)*(-c + x4))/(4*r1^2 + (-c + d)^2))^2,  # eq4
       -r2^2 + (-b + b*(-b*(-b + x2) + 2*r1*(2*r1 - r2))/(b^2 + 4*r1^2) + x2)^2 + (2*r1 - 2*r1*(-b*(-b + x2) + 2*r1*(2*r1 - r2))/(b^2 + 4*r1^2) - r2)^2,  # eq5
       -r3^2 + (-2*r1*(-b*(-b + r3) + 2*r1*r3)/(b^2 + 4*r1^2) + r3)^2 + (-b + b*(-b*(-b + r3) + 2*r1*r3)/(b^2 + 4*r1^2) + r3)^2,  # eq6
       -r4^2 + (-2*r1*(-b*(-b + x4) + 2*r1*r4)/(b^2 + 4*r1^2) + r4)^2 + (-b + b*(-b*(-b + x4) + 2*r1*r4)/(b^2 + 4*r1^2) + x4)^2,  # eq7
       -r1/(a - r1) + r2/x2,  # eq8
   ]
end;

(r2, r4) = (44, 33)./2
iniv = BigFloat[205, 155, 40, 150, 42, 90, 30, 90]
res = nls(H, ini=iniv)

   (BigFloat[209.9999999999999999999999999999999999999999999999999999999999999998827654490999, 157.4999999999999999999999999999999999999999999999999999999999999999096530095862, 41.99999999999999999999999999999999999999999999999999999999999999999764231208424, 153.9999999999999999999999999999999999999999999999999999999999999998816882373083, 42.0000000000000000000000000000000000000000000000000000000000000000018357614881, 87.99999999999999999999999999999999999999999999999999999999999999994964199517249, 31.49999999999999999999999999999999999999999999999999999999999999999749742450348, 91.49999999999999999999999999999999999999999999999999999999999999994744891428587], true)

元円，利円の半径はそれぞれ 42, 31.5 である。
したがって，亨円，貞円の直径がそれぞれ 44 寸，33 寸のとき，利円の直径は 63 寸である。

その他のパラメータは以下の通りである。

   a = 210;  b = 157.5;  c = 42;  d = 154;  r1 = 42;  r2 = 22;  x2 = 88;  r3 = 31.5;  r4 = 16.5;  x4 = 91.5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, c, d, r1, x2, r3, x4) = [189, 113, 52, 100, 54, 62, 32, 76]
   (a, b, c, d, r1, x2, r3, x4) = res[1]
   (r2, r4) = (44, 33)./2
   println("利円の直径 = $(round(Int, Float64(2r3)))")
   @printf("a = %g;  b = %g;  c = %g;  d = %g;  r1 = %g;  r2 = %g;  x2 = %g;  r3 = %g;  r4 = %g;  x4 = %g\n", a, b, c, d, r1, r2, x2, r3, r4, x4)
   plot([0, a, a, 0, 0], [0, 0, 2r1, 2r1, 0], color=:black, lw=0.5)
   circle(a - r1, r1, r1)
   circle(x2, 2r1 - r2, r2, :blue)
   circle(r3, r3, r3, :green)
   circle(x4, r4, r4, :magenta)
   segment(b, 0, 0, 2r1)
   segment(c, 0, d, 2r1)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(a - r1, r1, "元円:r1,(a-r1,r1)", :red, :center, delta=-2delta)
       point(x2, 2r1 - r2, "亨円:r2\n(x2,2r1-r2", :blue, :center, :bottom, delta=2delta)
       point(r3, r3, "利円:r3,(r3,r3)", :green, :center, delta=-2delta)
       point(x4, r4, "貞円:r4,(x4,r4)", :black, :center, delta=-2delta)
       point(a, 0, "a", :black, :center, :top, delta=-delta)
       point(b, 0, "b", :black, :center, :top, delta=-delta)
       point(c, 0, "c", :black, :center, :top, delta=-delta)
       point(d, 2r1, "(d,2r1)", :black, :center, :bottom, delta=delta)
       point(0, 2r1, " 2r1", :black, :left, :bottom, delta=delta)
       plot!(ylims=(-10, 90))
   end
end;

算額（その685）

算額（その685）

和算問題あれこれ 2 令和5年2月の問題-No.4（『算法求積通考』第6問）
https://gunmawasan.web.fc2.com/k-n-mondai.html

長径 2 寸，短径 1 寸の楕円形の周は何寸か。
小数点以下 4 位を四捨五入し，小数点以下 3 位まで答えよ。
円周率は 3.14159 を使用のこと。

コンピュータを使って正確な値を求めるならば，第二種完全楕円積分を使えばよい。
計算するためのパッケージ（ライブラリ）が用意されているのでそれを使えばよい。あるいは，区分求積法を使ってもよいし，逐次計算により求めてもよい。

しかし，今回のように要求される精度がほどほどに指定されている場合には，いくつかの近似式があるので精度に基づいて選択すればよい。

以下では，楕円のパラメータとして，長半径 a，短半径 b を使う。
長半径，短半径は長径，短径の半分である。

a = 2//2   # 長径 2
b = 1//2;  # 短径 1

まずは，関孝和の近似式

2sqrt(4(a - b)^2 + 3.14159^2*a*b)

    4.872286471072899

第二種完全楕円積分の近似式で，Gauss-Kummer の公式

h = (a - b)/(a + b)
3.14159*(a + b)*(1 + (h/2)^2 + h^4/64 + h^6/256)

    4.844218858908822

同じく近似式でシュリニヴァーサ・アイヤンガー・ラマヌジャンの近似式

3.14159*(3(a + b) - sqrt((3a + b)*(a + 3b)))

    4.844206457106038

名前が似ているが，もう少し精度が高いらしい，シュリニヴァーサ・ラマヌジャンの近似式

3.14159* (a + b)*(1 + 3*((a - b)/(a + b))^2/(10 + sqrt(4 - 3*((a - b)/(a + b))^2)))

    4.844220016323984

残念ながら，関孝和の近似式はちょっと精度が足りないが，他の近似公式では「小数点以下 4 位を四捨五入し，小数点以下 3 位まで答えよ」の要件を満たし，4.844 を与える。

なお，第二種完全楕円積分を用いた正確な値は 4.844224110273837 である。

using Elliptic
m = 1.0 - (b / a)^2             # 楕円の離心率を計算
println(4 * a * ellipke(m)[2])  # 楕円の周長を計算(第二種完全楕円積分）

    4.844224110273837

算額（その684）

算額（その684）

和算問題あれこれ 2 令和5年2月の問題-No.2（茨城県 板橋不動願成寺）
https://gunmawasan.web.fc2.com/k-n-mondai.html

正三角形の中に，大円，中円，小円が入っており，中円と小円の共通接線となる斜線がある。
小円の直径が 9 寸のとき，中円の直径を求めよ。

正三角形の左の頂点を原点とする
正三角形の一辺の長さを a
大円の半径と中心座標を r1, (a/2, r1); r1 = √3*a/6
中円の半径と中心座標を r2, (a/2, 2r1 + r2)
小円の半径と中心座標を r3, (x3, y3)
斜線と正三角形の交点座標を (x1, y1) 
とおき，以下の連立方程式を解く。

(1)　まず，正三角形の一辺の長さ a と，大円，中円の半径 r1, r2 の関連を知る。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, r1::positive, r2::positive

sqrt3 = sqrt(Sym(3))
eq1 = (sqrt3*a/2 - r1)/2 - r1
eq2 = (sqrt3*a/2 - 2r1 - r2)/2 - r2
solve([eq1, eq2], (r1, r2))

   Dict{Any, Any} with 2 entries:
     r1 => sqrt(3)*a/6
     r2 => sqrt(3)*a/18

(2)　次に，小円の半径がわかっているので，小円の中心座標 (x3, y3) と正三角形の一辺の長さ a を求める

@syms a::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     x1::positive
y1 = sqrt3*(a - x1)
r1 = sqrt3*a/6
r2 = r1/3
r3 = 9//2

eq3 = (a/2 - x3)^2 + (sqrt3*a/6 - y3)^2 - (r1 + r3)^2
eq5 = y3*a/2 - (2r1 + r2)*x3
eq6 = (a/2 - 2sqrt(r1*r3))*r2 - (a/2 +  2sqrt(r1*r2))*(9//2);

res = solve([eq3, eq5, eq6], (a, x3, y3))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (75*sqrt(3), 27*sqrt(3)/2, 63/2)
    (75*sqrt(3), 1287*sqrt(3)/38, 3003/38)

2 組の解が得られるが，最初のものが適解である。

(3)　最後に斜線と正三角形の交点座標 (x1, y1) を求める。

@syms a::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     x1::positive
(a, x3, y3) = (75*sqrt3, 27*sqrt3/2, 63//2)
y1 = sqrt3*(a - x1)
(r1, r2, r3) = (sqrt3*a/6, sqrt3*a/18, 9//2)
eq4 = dist(0, 0, x1, y1, a/2, 2r1 + r2) - r2^2
res2 = solve(eq4)
res2 |> println

   Sym[75*sqrt(3)/2, 325*sqrt(3)/7]

2番目のものが適解である。x1 = 325√3/7 = 80.4166446371264

x1 = res2[2].evalf()
x1 |> println

   80.4166446371264

y 座標値は y1 = √3(a - x1) = 85.7142857142857

y1 = √3(a - x1).evalf()
y1 |> println

   85.7142857142857

以上のパラメータをまとめると以下のようになる。

   中円の直径 = 25;  a = 129.904;  r1 = 37.5;  r2 = 12.5;  r3 = 4.5;  x3 = 23.3827;  y3 = 31.5;  x1 = 80.4166;  y1 = 85.7143

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   sqrt3 = √3
   (a, x3, y3) = (75√3, 27√3/2, 63/2)
   (r1, r2, r3) = (√3a/6, √3a/18, 9/2)
   x1 = 325*sqrt(3)/7
   y1 = sqrt3*(a - x1)
   @printf("中円の直径 = %.15g;  a = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  y3 = %g;  x1 = %g;  y1 = %g\n",
       2r2, a, r1, r2, r3, x3, y3, x1, y1)
   plot([0, a, a/2, 0], [0, 0, sqrt3*a/2, 0], color=:black, lw=0.5)
   circle(a/2, r1, r1)
   circle(a/2, 2r1 + r2, r2, :blue)
   circle(x3, y3, r3, :green)
   segment(0, 0, x1, y1, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(a/2, r1, "大円:r1,(a/2,r1)", :red, :center, delta=-delta)
       point(a/2, 2r1 + r2, "中円:r2,(a/2,2r1+r2) ", :blue, :right, :vcenter)
       point(x3, y3, " 小円:r3,(x3,y3)", :blue, :left, :top, delta=-2delta)
       point(a, 0, " a", :black, :left, :bottom, delta=delta/2)
       point(a/2, 0, "a/2", :black, :center, :bottom, delta=delta/2)
       point(a/2, √3a/2, "(a/2,√3a/2)", :black, :left, :bottom, delta=delta/2)
       point(x1, y1, " (x1,y1)", :black, :left, :vcenter)
   end
end;

算額（その683）

算額（その683）

和算問題あれこれ 2 令和5年2月の問題-No.1（茨城県 板橋不動願成寺）
https://gunmawasan.web.fc2.com/k-n-mondai.html

直角三角形の中に正方形，長方形，等円 2 個がある。
鈎，股 がそれぞれ 27 寸，36 寸のとき，等円の直径を求めよ。

この問題は，算額（70）
https://blog.goo.ne.jp/r-de-r/e/071461791de5889b7aaceea141d47ced
東京都府中市 大国魂神社
http://www2.ttcn.ne.jp/~nagai/sangaku/sangakumondai1.htm
のものに似ているが，鈎，股に接する等円が正方形，長方形との接し方に違いがある。

式の記述を簡単にするために，問の図を左右を反転させた図で考える。

鈎，股，弦の長さをを「鈎」，「股」，「弦」
長方形の長辺，短辺の長さを「長」，「短」
正方形の一辺の長さを「方」
等円のと中心座標を「径」，(x1, 短 + 径/2)
として，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     方::positive, 長::positive, 短::positive, 径::positive,
     x1

(鈎, 股) = (Sym(27), Sym(36))
弦 = sqrt(鈎^2 + 股^2)
eq1 = (1 + 4//3 - 5//3)方 - 径
eq2 = 鈎 - (5//4 + 3//5)*方 - 短
eq3 = (弦 - (3//4 + 1 + 4//3)*方)^2 - 短^2 - (股 - 径 - 長)^2
eq4 = dist(4方/5, 短, 0, 鈎 - 5方/4, 径/2, 径/2) - 径^2/4
eq5 = dist(股, 0, 0, 鈎, x1, 短 + 径/2) - 径^2/4
res = solve([eq1, eq2, eq3, eq4, eq5], (方, 長, 短, 径, x1))

   4-element Vector{NTuple{5, Sym}}:
    (12, 108/5, 24/5, 8, 88/5)
    (12, 108/5, 24/5, 8, 464/15)
    (12, 172/5, 24/5, 8, 88/5)
    (12, 172/5, 24/5, 8, 464/15)

4 組の解が得られるが，最初のものが適解である。

鈎，股 が 27寸, 36寸のとき，等円の直径は 8 寸である。

正方形の一辺の長さは 12寸，長方形の長辺，短辺の長さはそれぞれ 108/5 = 21.6寸，24/5 = 4.8寸である。

大国魂神社の算額と比較すると，鈎股に接する等円と長方形の短辺が接するように長方形の長辺を長くしただけであることがわかる。

using Plots

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股) = (27, 36)
   弦 = sqrt(鈎^2 + 股^2)
   (方, 長, 短, 径, x1) = (12, 108/5, 24/5, 8, 88/5)
   r = 径/2
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:black, lw=0.5)
   circle(r, r, r)
   circle(x1, 短 + r, r)
   rect(2r + 長, 0, 2r, 短, :blue)
   plot!([4方/5, 0, 3方/5, 7方/5, 4方/5],
       [短, 鈎 -5方/4, 鈎 - 9方/20, 鈎 - 21方/20, 短], color=:green, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(股, 0, " 股", :black, :left, :bottom, delta=delta)
       point(0, 鈎, " 鈎", :black, :left, :bottom, delta=delta/2)
       point(r, r, "等円:r,(r,r)", :red, :center, delta=-delta)
       point(x1, 短 + r, "等円:r\n(x1,短+r)", :red, :center, delta=-delta)
       point(2r + 長, 0, " 2r+長", :blue, :left, :bottom, delta=delta)
       point(4方/5, 短, "a", :green, :center, delta=-delta)
       point(0, 鈎 -5方/4, "  b", :green, :left, :vcenter)
       point(3方/5, 鈎 - 9方/20, " c", :green, :left, :bottom)
       point(7方/5, 鈎 - 21方/20, " d", :green, :left, :bottom)
   end
end;

 

算額（その682）

算額（その682）

 

愛媛県 大洲市新谷 法眼寺 寛政6年(1794)11月
http://www.wasan.jp/ehime/hogenji.html

埼玉県比企郡鳩山町 円正寺不動堂 文政 11 年(1828)8月
http://www.wasan.jp/saitama/ensyoji.html

山口正義：やまぶき 第18号
https://yamabukiwasan.sakura.ne.jp/ymbk18.pdf
山口正義：やまぶき 第19号
https://yamabukiwasan.sakura.ne.jp/ymbk19.pdf
山口正義：円正寺の算額の謎（鳩山町）
https://yamabukiwasan.sakura.ne.jp/23enshoujisanga.pdf

(5) 大阪府池田市畑 畑天満宮 嘉永5年(1852)晩夏
近畿数学史学会：近畿の算額「数学の絵馬を訪ねて」，平成4年5月16日 初版第一刷，大阪教育図書株式会社，大阪市.

大阪府池田市 畑天満宮 嘉永5年(1852)晩夏
http://www.wasan.jp/osaka/hata.html

八七 加須市大越六間 天神社 明治14年(1881)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

百四十一 群馬県藤岡市鮎川 北野神社 明治24年(1891)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.

和算問題あれこれ 2 令和6年2月の問題-No.2
https://gunmawasan.web.fc2.com/k-n-mondai.html

東京都日本橋 福徳神社（芽吹稲荷）
https://mebuki.jp/2125/

キーワード：円1個，直角三角形，正方形
#Julia, #SymPy, #算額, #和算, #数学

中円の周りに等円 5 個が互いに接している。中円の直径が 17.55 寸のとき，等円の直径はいかほどか。

この算額は，算額（その29）から外円を除いたものである。

等円の直径だけを求めるならば，公式3の(2) （注）より，

等円の直径 = 中円の直径/(sqrt(50 + 10sqrt(5))/5 - 1) = 25.024895967700825 寸である。

17.55/(sqrt(50 + 10sqrt(5))/5 - 1) |> println

   25.024895967700825

注：中村信弥編著: 和算の図形公式--『算法助術』--- 
　　http://www.wasan.jp/kosiki/kosiki.html

中円の中心座標を r1, (0, 0)
等円の半径と中心座標を r2, (x2, y2), (0, r1 + r2)
とおき，以下の連立方程式を解き，r1 を与えて r2，x2，y2 を得る。
式が長くなるので cos(18°), sin(18°) を c18，s18 とておく。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r1::positive, r2::positive, x2::positive, y2::positive
@syms c18, s18
eq1 = x2 - (r1 + r2)c18;
eq2 = y2 - (r1 + r2)s18;
eq3 = x2^2 + (r1 + r2 - y2)^2 - 4r2^2;

res = solve([eq1, eq2, eq3], (r2, x2, y2))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (r1*(-c18^2 - s18^2 + 2*s18 - 2*sqrt(c18^2 + s18^2 - 2*s18 + 1) - 1)/(c18^2 + s18^2 - 2*s18 - 3), -2*c18*r1*(sqrt(c18^2 + s18^2 - 2*s18 + 1) + 2)/(c18^2 + s18^2 - 2*s18 - 3), -2*r1*s18*sqrt(c18^2 + s18^2 - 2*s18 + 1)/(c18^2 + s18^2 - 2*s18 - 3) - 4*r1*s18/(c18^2 + s18^2 - 2*s18 - 3))
    (r1*(-c18^2 - s18^2 + 2*s18 + 2*sqrt(c18^2 + s18^2 - 2*s18 + 1) - 1)/(c18^2 + s18^2 - 2*s18 - 3), 2*c18*r1*(sqrt(c18^2 + s18^2 - 2*s18 + 1) - 2)/(c18^2 + s18^2 - 2*s18 - 3), 2*r1*s18*sqrt(c18^2 + s18^2 - 2*s18 + 1)/(c18^2 + s18^2 - 2*s18 - 3) - 4*r1*s18/(c18^2 + s18^2 - 2*s18 - 3))

2通りの解が得られるが，最初のものが適解である。

式は長いが，以下のように簡約化できる。

c18 = cosd(18)  # cos(π/10)
s18 = sind(18)  # sin(π/10)
天 = 1 - 2*s18
地 = 3 - 天
人 = sqrt(天 + 1)
とおいて，r1 が与えられれば，r2, x2, y2 は以下のようにして計算される。
r2 = r1*(天 + 2人 + 1)/地
x2 = r1*2c18*(人 + 2)/地
y2 = r1*2s18*(人 + 2)/地

   等円の直径 = 25.02489596770083
   等円の直径 = 25.0249;  r1 = 8.775;  r2 = 12.5124;  x2 = 20.2456;  y2 = 6.57818

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 17.55/2
   # r1 = 17.5325404176020/2
   c18 = cosd(18)  # cos(π/10)
   s18 = sind(18)  # sin(π/10)
   天 = 1 - 2*s18
   地 = 3 - 天
   人 = sqrt(天 + 1)
   (r2, x2, y2) = r1 .* ( (天 + 2人 + 1)/地,  2c18*(人 + 2)/地,  2s18*(人 + 2)/地)
   println("等円の直径 = $(2r2)")
   @printf("等円の直径 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n",
       2r2, r1, r2, x2, y2)
   plot()
   r0 = r1 + r2
   circle(0, 0, r1, :green)
   circle(0, r0, r2)
   circle(r0*cos(pi/10), r0*sin(pi/10), r2)
   circle(-r0*cos(pi/10), r0*sin(pi/10), r2)
   circle(r0*cos(17pi/10), r0*sin(17pi/10), r2)
   circle(-r0*cos(17pi/10), r0*sin(17pi/10), r2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(0, 0, "0 ", :black, :right)
       point(0, r1 + r2, "r1+r2 ", :red, :right)
       point(0, r1, "r1 ", :green, :right, :bottom, delta=delta/2)
       point(x2, y2, "等円:r2,(x2,y2)", :magenta, :center)
       vline!([0], color=:black, linewidth=0.25)
       hline!([0], color=:black, linewidth=0.25)
   end
end;

算額（その681）

算額（その681）

山口正義: やまぶき4，第58号，2018/12/06.
千葉県君津市鹿野山 鹿野山神野寺 万延二年(1861)
https://yamabukiwasan.sakura.ne.jp/ymbk58.pdf
山口正義：やまぶき，和算と歴史随想 からリンク
https://yamabukiwasan.sakura.ne.jp/page3.html

短径が 3 寸の楕円の中に，直径 2寸4分の等円が 2 個入っている。楕円の周長はいかほどか。ただし，円積率として 7分8厘5毛4糸を使うものとする。

楕円の長半径，短半径，中心座標を a, b, (0, 0)
等円の半径と，中心座標を r, (r, 0)
楕円と等円の接点の座標を (x1, y1)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a::positive, b::positive, r::positive, x1::positive, y1::positive

eq1 = (x1 - r)^2 + y1^2 - r^2
eq2 = -b^2*x1/(a^2*y1) - (r - x1)/y1
eq3 = x1^2/a^2 + y1^2/b^2 - 1
res = solve([eq1, eq2, eq3], (x1, y1, a))

   2-element Vector{Tuple{Sym, Sym, Sym}}:
    (b^2/r, b*sqrt(-b^2 + 2*r^2)/r, -b^2*sqrt(1/(b^2 - r^2)))
    (b^2/r, b*sqrt(-b^2 + 2*r^2)/r, b^2*sqrt(1/(b^2 - r^2)))

2 組の解が得られるが，2 番目のものが適解である（最初のものは x 軸に関して線対称な解である）。

x1, y2, a はそれぞれ短半径 b の b/r 倍，sqrt(2r^2 - b^2) 倍，b/sqrt(b^2 - r^2) 倍である。

短径（差渡し径）が 3 寸（短半径が 1.5 寸），等円の直径が 2.4 寸のとき，長半径は 2.5 寸である（差渡し径 5 寸）。

   b = 1.5;  r = 1.2;  x1 = 1.875;  y1 = 0.992157;  a = 2.5

楕円の周長は第二種完全楕円積分による正確な値として 12.763499431699064 が得られる。

問において，「円周率は 0.7854 を使う」とあるのは，円積率のことで円周率になおすと 3.1416 である。当時，円積率としては 0.79（円周率は 3.16）が使われることが多かったであろうにしては，正確すぎる。
しかし，この円積率を使ったとしても，「答」にある 12.7634994317113 有奇を導いた近似式などが不明（術を読み解く力がない）。有効数字 11 桁が一致している。驚異的。

長径と短径の比がきれいな値なので，事前に計算された数表などがあったのかもしれない。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (b, r) = (3//2, 24/20)
   (x1, y1, a) = b .* (b/r, sqrt(2r^2 - b^2)/r, b/sqrt(b^2 - r^2))
   @printf("b = %g;  r = %g;  x1 = %g;  y1 = %g;  a = %g\n", b, r, x1, y1, a)
   plot()
   ellipse(0, 0, a, b, color=:blue)
   circle(r, 0, r)
   circle(-r, 0, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       vline!([0], color=:black, lw=0.5)
       hline!([0], color=:black, lw=0.5)
       point(x1, y1, " (x1,y1)", :black, :left, :bottom)
       point(r, 0, "r", :red, :center, :bottom, delta=delta)
       point(0, b, " b", :blue, :left, :bottom, delta=delta)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta)
   end
end;