おさらいの続き

さてさて、脳トレの一環として記憶力と思考力を使う機会をってことで電験１種に挑もうなどと無謀なことを考えついたわけですが、前に電験２種のおさらいとして受電円をアップしました。まぁベクトル図も円線図も間違いだらけｗ読む人には間違い探しを通じて脳トレ出来るんじゃないかｗってぐらいです。

今回も電験２種の内容のおさらいです。

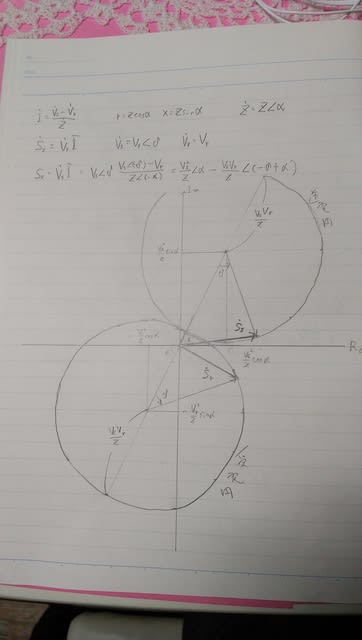
受電円が描けたら同じ要領で送電円も描ける。二つのマルを同じ複素平面に描いたのが電力円線図ってわけです。

受電円の中心は－Vr^2/Z∠α　半径はVsVr/Z

送電円の中心は+Vs^2/Z∠α　半径はVsVr/Z

ここで、大抵Vs＞Vrなことが多いですから、そんな場合は原点から中心までの距離は送電円が大きくなる。半径はどちらも同じ。中心を結ぶ線は原点を通り、実軸との角度は送電線のインピーダンスの偏角α。２つの円は接することになる。

そして、それぞれの円の上を送電端、受電端の皮相電力ベクトルは独自に軌跡を描くのではなく、２つの円の中心を結ぶ線との角度が相差角δとなるように軌跡を描く。このことから送電端と受電端の皮相電力が視覚的に分かるわけです。実軸成分の差が送電線の抵抗によるロス分です。

ここで、ホントに半径が一緒？接するだけじゃなくって交わったり離れたりすることは？って疑問を抱かれた方は鋭い！さっき述べた円線図の法則には理由がある。結局送電端と受電端で同じ電流が流れているからそうなるんです。

実際の送電線は漏れ電流、充電電流が流れます。特にケーブルなんかではこうした電流を無視できない。そうなると円線図は半径が異なって交わったりする。教本にもそのようなアドミタンスを考慮したケースの円線図が解説されてて、こっからいよいよ電験１種の範疇の学習に突入します。まぁ、音を上げるのは時間の問題のような気もしますが、老化防止の脳トレなんで焦らずぼちぼち学びを進めることにします。

 

※これから電験２種を取ろうとされている方々へ

おそらくアドミタンスを考慮した円線図は電験２種では出題されないものと信じてますけど、もし出題されてしまったら地に伏して謝るしかないですねｗ。とはいってもそんな問題が出題される確率はメチャメチャ低いですし、出題されたらそんな問題は選択しないことです。幸い６問中４問選んで６割得点できたらいいんです。アドミタンス考慮の電力円線図なんて電験２種の試験問題には難しすぎます。