算額（その746）

算額（その746）

七七 大里郡大里村相上 吉見神社 明治9年(1876)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

埼玉県北本市本宿 天神社 明治24年(1891)
山口正義：やまぶき2，第41号
https://yamabukiwasan.sakura.ne.jp/ymbk41.pdf

キーワード：円5個，外円

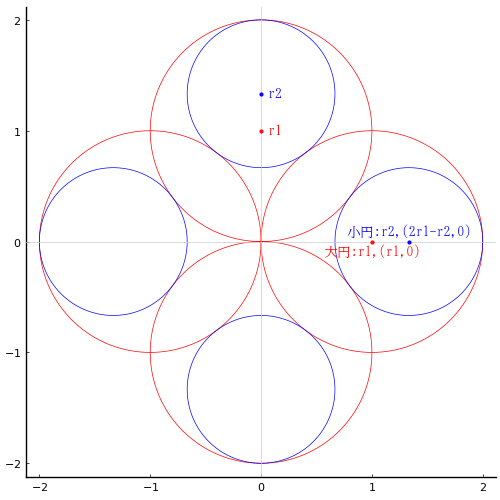
外円の中に大円，小円が 1 個ずつ，中円が 2 個入っている。外円，大円，小円の直径がそれぞれ 4 寸，2 寸 4 分，9 分のとき，中円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, r1 - R)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (0, R - r3)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     x2::positive, y2::positive, r3::positive
eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = x2^2 + (y2 - r1 + R)^2 - (r1 + r2)^2
eq3 = x2^2 + (R - r3 - y2)^2 - (r2 + r3)^2
res = solve([eq1, eq2, eq3], (r2, x2, y2))

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (-R*(-R + r1)*(-R + r3)/(-R^2 + r1*r3), -2*R*sqrt(r1)*sqrt(r3)*sqrt((-R + r1)*(-R + r3))/(-R^2 + r1*r3), -R^2*(r1 - r3)/(-R^2 + r1*r3))
    (-R*(-R + r1)*(-R + r3)/(-R^2 + r1*r3), 2*R*sqrt(r1)*sqrt(r3)*sqrt((-R + r1)*(-R + r3))/(-R^2 + r1*r3), -R^2*(r1 - r3)/(-R^2 + r1*r3))

2 組の解が得られる。x2 の符号が違うだけで，本質的にどちらも適解であるが，符号の点で最初のものを採用する。

中円の半径は，R*(R - r1)*(R - r3)/(R^2 - r1*r3) となる。

res[1][1] |> simplify |> println

   R*(R - r1)*(R - r3)/(R^2 - r1*r3)

外円，大円，小円の直径がそれぞれ 4 寸，2 寸 4 分，9 分のとき，中円の半径は 0.7167630057803468 である。直径は 1.4335260115606936 である。

(R, r1, r3) = (40, 24, 9) ./ 20
r2 = R*(R - r1)*(R - r3)/(R^2 - r1*r3)
(r2, 2r2)

   (0.7167630057803469, 1.4335260115606938)

「術」では「大小円径を乗じ，外円径の二乗から引いたもので，外大円径の差と外小円径の差と外円径を乗じたものを割る」と得られた式と同じことを書いているのだが，どこかで計算違いをしたのか「答」では 1 寸 5 分となっている。

その他のパラメータは以下のとおり。

   中円の直径 = 1.43353;  R = 2;  r1 = 1.2;  r3 = 0.45;  r2 = 0.716763;  x2 = 0.946001;  y2 = 0.867052

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r1, r3) = (40, 24, 9) .// 20
   (r2, x2, y2) = (-R*(-R + r1)*(-R + r3)/(-R^2 + r1*r3), -2*R*sqrt(r1)*sqrt(r3)*sqrt((-R + r1)*(-R + r3))/(-R^2 + r1*r3), -R^2*(r1 - r3)/(-R^2 + r1*r3))
   @printf("中円の直径 = %g;  R = %g;  r1 = %g;  r3 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", 2r2, R, r1, r3, r2, x2, y2)
   plot()
   circle(0, 0, R, :magenta)
   circle(0, r1 - R, r1, :blue)
   circle2(x2, y2, r2)
   circle(0, R - r3, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1 - R, " 大円:r1,(0,r1-R)", :blue, :center, delta=-delta/2)
       point(x2, y2, "中円:r2,(x2,y2)", :red, :center, delta=-delta/2)
       point(0, R - r3, "小円:r3\n(0,R-r3)", :green, :center, delta=-delta/2)
       point(R, 0, " R", :magenta, :left, :vcenter)
   end
end;

算額（その745）

算額（その745）

埼玉県北本市本宿 天神社 明治24年(1891)
山口正義：やまぶき2，第41号
https://yamabukiwasan.sakura.ne.jp/ymbk41.pdf

直線の上に大円 1 個と中円 2 個が載り，中円の上に小円が載っている。
大円，中円の直径をそれぞれ 4 寸，2 寸 4 分としたとき，小円の直径はいかほどか。

大円の半径と中心座標を r1, (0, r1)
中円の半径と中心座標を r2, (r2, r2)
小円の半径と中心座標を r3, (0, 2r1 - r3)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive
eq = r2^2 + (2r1 - r3 - r2)^2 - (r2 + r3)^2
res = solve(eq, r3)

   1-element Vector{Sym{PyCall.PyObject}}:
    (2*r1 - r2)^2/(4*r1)

小円の直径は，2(2*r1 - r2)^2/(4*r1) である。
大円，中円の直径をそれぞれ 4 寸，2 寸 4 分としたとき，小円の直径は 49/25 寸 = 1 寸 9 分 6 厘である。

「術」は，「中円の直径を二乗したものを大円の直径の4倍で割り，大円と中円の直径の差を加える d2^2/4d1 + (d1 - d2)」と同じことを指している。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (40, 24) .// 20
   r3 = (2*r1 - r2)^2/(4*r1)
   @printf("小円の直径 = %g;  r1 = %g;  r2 = %g;  r3 = %g\n", 2r3, r1, r2, r3)
   plot()
   circle2(r2, r2, r2, :green)
   circle(0, r1, r1, :blue)
   circle(0, 2r1 - r3, r3)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, " 大円:r1,(0, r1)", :blue, :left, :vcenter)
       point(r2, r2, "中円:r2,(r2,r2)", :green, :center, delta=-delta/2)
       point(0, 2r1 - r3, " 小円:r3\n (0,2r1-r3)", :red, :left, :vcenter)
   end
end;

算額（その744）

算額（その744）

重複していただけでなく，8 個の乙円と言われているのに 6 個しか描いていなかった。乙円の直径は正しく計算されている。
ということで，算額（その898）を参照のこと。

埼玉県北本市本宿 天神社 明治24年(1891)
山口正義：やまぶき2，第41号
https://yamabukiwasan.sakura.ne.jp/ymbk41.pdf

大円と甲円 4 個が交わっている領域に 8 個の乙円が入っている。甲円の直径が 2 寸のとき，乙円の直径はいかほどか。

大円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (r1, r1)
乙円の半径と中心座標を r2, (R  - r2, 0), ((r1 + r2)√2, (r1 + r2)√2)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive
r1 = 2//2
x2 = r1 + (r1 - r2)/sqrt(Sym(2))  # こちらの定義を使わないと適切な解にならない
y2 = x2
eq1 = (R - r2 - r1)^2 + r1^2 - (r1 + r2)^2
eq2 = x2^2 + y2^2 - (R + r2)^2
res = solve([eq1, eq2], (r2, R));

3 組の解が得られるが，最初のものが適解である。なお，SymPy による解は虚数として得られるが虚部は実質 0 なので，実部のみを取るか絶対値を取ればよい。

甲円の直径が 2 寸のとき，乙円の直径は 0.463411633339116 寸である。

res[1]

   (1 + (1 - sqrt(2))*(-sqrt(2)/6 + 1/6 - (-1/2 + sqrt(3)*I/2)*(83/8 + 59*sqrt(2)/8 + sqrt(-4*(27/4 + 11*sqrt(2)/2)^3 + (83/4 + 59*sqrt(2)/4)^2)/2)^(1/3)/3 - (27/4 + 11*sqrt(2)/2)/(3*(-1/2 + sqrt(3)*I/2)*(83/8 + 59*sqrt(2)/8 + sqrt(-4*(27/4 + 11*sqrt(2)/2)^3 + (83/4 + 59*sqrt(2)/4)^2)/2)^(1/3)))^2 + (-1 + sqrt(2))*(-sqrt(2)/6 + 1/6 - (-1/2 + sqrt(3)*I/2)*(83/8 + 59*sqrt(2)/8 + sqrt(-4*(27/4 + 11*sqrt(2)/2)^3 + (83/4 + 59*sqrt(2)/4)^2)/2)^(1/3)/3 - (27/4 + 11*sqrt(2)/2)/(3*(-1/2 + sqrt(3)*I/2)*(83/8 + 59*sqrt(2)/8 + sqrt(-4*(27/4 + 11*sqrt(2)/2)^3 + (83/4 + 59*sqrt(2)/4)^2)/2)^(1/3))), -sqrt(2)/6 + 1/6 - (-1/2 + sqrt(3)*I/2)*(83/8 + 59*sqrt(2)/8 + sqrt(-4*(27/4 + 11*sqrt(2)/2)^3 + (83/4 + 59*sqrt(2)/4)^2)/2)^(1/3)/3 - (27/4 + 11*sqrt(2)/2)/(3*(-1/2 + sqrt(3)*I/2)*(83/8 + 59*sqrt(2)/8 + sqrt(-4*(27/4 + 11*sqrt(2)/2)^3 + (83/4 + 59*sqrt(2)/4)^2)/2)^(1/3)))

for i in 1:length(res)
   println("r2 = $(abs(res[i][1](r1=>1).evalf()));  R = $(abs(res[i][2](r1=>1).evalf()))")
end

   r2 = 0.231705816669558;  R = 1.95080192903398
   r2 = 1.07895435511026;  R = 0.256304852152569
   r2 = 2.41421356237309;  R = 2.41421356237309

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 2/2
   (r2, R) = (0.231705816669558, 1.95080192903398)
   x2 = r1 + (r1 - r2)/sqrt(2)
   # x2 = (2r1 - r2)/sqrt(2)  # 代替
   # x2 = (R + r2)/sqrt(2)
   y2 = x2
   @printf("小円の直径 %g;  大円の直径 = %g;  外円の直径 = %g\n", 2r2, 2r1, 2R)
   plot()
   circle(0, 0, R, :green)
   circle4(r1, r1, r1, :blue)
   circle2(R - r2, 0, r2)
   circle4((R + r2)/√2, (R + r2)/√2, r2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
       point(r1, r1, "甲円:r1,(r1,r1)", :blue, :center, delta=-delta/2)
       point(x2, y2, "乙円:r2,(x2,y2) ", :black, :right, :vcenter)
       point(R - r2, 0, "R-r2 ", :black, :right, :vcenter)
   end
end;

算額（その743）

算額（その743）

埼玉県北本市本宿 天神社 明治24年(1891)
山口正義：やまぶき2，第41号
https://yamabukiwasan.sakura.ne.jp/ymbk41.pdf

九五 大里郡江南村野原 文殊寺 明治24年(1891)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

大円 6 個が環状に外接し合って並び，内側に 3 個の小円が互いに外接すると同時に大円にも外接している。
大円の直径が 1 寸 5 分のとき，小円の直径はいかほどか。
（注：図では小円の位置関係がはっきりしないが，上述のようでなければ算額としての価値がない）

大円の半径と中心座標を r1, (2r1, 0), (0, r1)
小円の半径と中心座標を r2, (r2, r2/√3)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive,
     x2::positive, y2::positive
#r1 = 15//20
x1 = 2r1
y2 = r2/sqrt(Sym(3))
eq = (x1 - r2)^2 + y2^2 - (r1 + r2)^2
res = solve(eq, r2)

   2-element Vector{Sym{PyCall.PyObject}}:
    3⋅r₁⋅(3 - 2⋅√2)
    3⋅r₁⋅(2⋅√2 + 3)

2 組の解が得られるが，最初のもの 3*r1*(3 - 2*sqrt(2)) が適解である。
小円の直径は，大円の直径の 3(3 - 2√2) 倍である。
「術」は「3️ から 8 の平方根を引き，3 倍して大円の直径を掛ける」ということで（当たり前ではあるが）一致する。

大円の直径が 1 寸 5 分のとき，小円の直径は 7 分 7 厘 2 毛である（「答」では 7 分 7 厘 3 毛となっているが）。

1.5 * 3(3 - 2√2)

   0.7720779386421437

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 15//20
   r2 = 3r1*(3 - 2√2)
   @printf("小円の直径 %g;  大円の直径 = %g\n", 2r2, 2r1)
   plot()
   rotate(2r1, 0, r1, angle=60)
   rotate(r2, r2/√3, r2, :blue, angle=120)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(2r1, 0, " 大円:r1,(2r1,0)", :red, :center, delta=-delta/2)
       point(r2, r2/√3, " 小円:r2,(r2,r2/√3)", :blue, :left, :vcenter)
   end
end;

算額（その742）

算額（その742）

埼玉県北本市本宿 天神社 明治24年(1891)
山口正義：やまぶき2，第41号
https://yamabukiwasan.sakura.ne.jp/ymbk41.pdf

一〇八 加須市騎西町 玉敷神社 大正4年(1915)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野

埼玉の算額108 埼玉県加須市騎西 玉敷神社 第4問
和算問題あれこれ2 令和６年４月の問題-No.１
https://gunmawasan.web.fc2.com/k-n-mondai.html

大円 4 個と小円 4 個が互いに交わり，かつ内接・外接している。
大円の直径が 2 寸のとき，小円の直径はいかほどか。

大円の半径と中心座標を r1, (r1, 0), (0, r1)
小円の半径と中心座標を r2, (2r1 - r2, 0)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive
eq = (2r1 - r2)^2 + r1^2 - (r1 + r2)^2
res = solve(eq, r2)

   1-element Vector{Sym{PyCall.PyObject}}:
    2*r1/3

小円の直径は大円の直径の 2/3 倍である。
大円の直径が 2 寸のとき，小円の直径は 4/3 寸 = 一寸三分三厘三毛有奇である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 2//2
   r2 = 2r1/3
   @printf("小円の直径 %g;  大円の直径 = %g\n", 2r2, 2r1)
   plot()
   circle42(0, r1, r1)
   circle42(0, 2r1 - r2, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(2r1 - r2, 0, "小円:r2,(2r1-r2,0)", :blue, :center, :bottom, delta=delta/2)
       point(r1, 0, "大円:r1,(r1,0)", :red, :center, delta=-delta/2)
       point(0, 2r1 - r2, " r2", :blue, :left, :vcenter)
       point(0, r1, " r1", :red, :left, :vcenter)
   end
end;