算額（その791）

算額（その791）

寛政十一年己未四月 丸山良玄門人 北越中宿邑 米持杢左衛門富房
藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

右鈎，左鈎，容円の直径が 9 寸，5 寸，3 寸のとき，雙股はいかほどか。

右鈎，左鈎，雙股 を R, L, a
容円の半径と中心座標を r, (x, r)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms x::positive, a::positive, d,

     r::positive, L::positive, R::positive
eq1 = dist(0, L, a, 0, x, r) - r^2
eq2 = dist(a, R, 0, 0, x, r) - r^2;
eq1 = numerator(apart(eq1, d))
eq2 = numerator(apart(eq2, d))
eq1 |> println
eq2 |> println

   L^2*a^2 - 2*L^2*a*x - L^2*r^2 + L^2*x^2 - 2*L*a^2*r + 2*L*a*r*x
   -R^2*r^2 + R^2*x^2 - 2*R*a*r*x

2 組の解が得られるが，最初のものが適解である。

右鈎，左鈎，容円の直径が 9 寸，5 寸，3 寸のとき，雙股は 112 寸である。

res = solve([eq1, eq2], (a, x));
res[1][1] |> println
res[1][1](L => 5, R => 9, r => 3//2) |> println

   2*r*sqrt((L - 2*r)/(L*R^2 - 4*L*R*r + 4*L*r^2 - 2*R^2*r + 4*R*r^2))*(-L*R + L*r + R*r)/(-L + 2*r)
   12

容円の中心座標は (9/2, 3/2) である。

res[1][2] |> println
res[1][2](L => 5, R => 9, r => 3//2) |> println

   R*r*sqrt((L - 2*r)/(L*R^2 - 4*L*R*r + 4*L*r^2 - 2*R^2*r + 4*R*r^2))
   9/2

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (L, R, r) = (5, 9, 3/2)
   (a, x) = (2*r*sqrt((L - 2*r)/(L*R^2 - 4*L*R*r + 4*L*r^2 - 2*R^2*r + 4*R*r^2))*(-L*R + L*r + R*r)/(-L + 2*r), R*r*sqrt((L - 2*r)/(L*R^2 - 4*L*R*r + 4*L*r^2 - 2*R^2*r + 4*R*r^2)))
   @printf("右鈎 = %g;  左鈎 = %g;  容円直径 = %g\n", R, L, 2r)
   @printf("雙股 = %g;  x = %g\n", a, x)
   plot([0, 0, a, 0, a, a, 0], [0, L, 0, 0, R, 0], color=:blue, lw=0.5)
   circle(x, r, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, R, "(a,R)", :blue, :right, :bottom, delta=delta/2)
       point(0, L, " R", :blue, :left, :bottom, delta=delta/2)
       point(x, r, "容円:r,(x,r)", :red, :center, delta=-delta/2)
       point(0, L/2, " 左鈎", :blue, :left, :vcenter, mark=false)
       point(a, R/2, "右鈎 ", :blue, :right, :vcenter, mark=false)
       point(a/2, 0, "雙股", :blue, :center, :bottom, delta=delta/2, mark=false)
   end
end;

算額（その790）

算額（その790）

寛政八年丙辰十一月 丸山因平良玄門人 参州苅屋 林政右衛門盛保 
藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

十字線を隔てて乾円，坤円，巽円，艮円の4円と，中央に容円を置く。艮円，坤円，巽円の直径がそれぞれ 15 寸，10 寸，6 寸のとき，乾円の直径を求めよ。

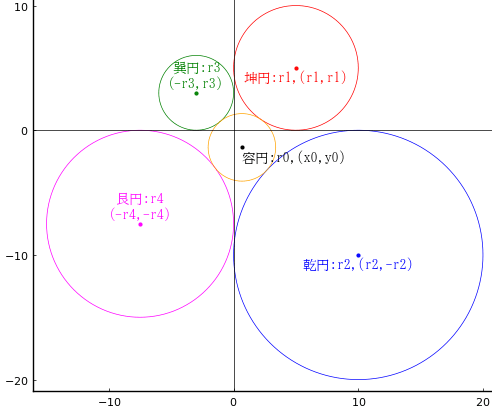
容円の半径と中心座標を r0, (x0, y0)
坤円の半径と中心座標を r1, (r1, r1)
乾円の半径と中心座標を r2, (r2, -r2)
巽円の半径と中心座標を r3, (-r3, r3)
艮円の半径と中心座標を r4, (-r4, -r4)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r0::positive, x0::negative, y0::positive,
     r1::positive, r2::positive, r3::positive, r4::positive
eq1 = (r1 - x0)^2 + (r1 - y0)^2 - (r0 + r1)^2
eq2 = (r2 - x0)^2 + (-r2 - y0)^2 - (r0 + r2)^2
eq3 = (-r3 - x0)^2 + (r3 - y0)^2 - (r0 + r3)^2
eq4 = (-r4 - x0)^2 + (-r4 - y0)^2 - (r0 + r4)^2
res = solve([eq1, eq2, eq3, eq4], (r2, r0, x0, y0));

4 番目の組が適解であるが，SymPy では簡約化できない長い式になる。

res[4][1] |> println

   sqrt(8*r1^2*r3*r4^2*(r1*r3 - r1*r4 + r3^2 + r3*r4)*(r1^2*r3 + r1^2*r4 + r1*r3^2 + 6*r1*r3*r4 - r1*r3*sqrt(r1^2 + 6*r1*r4 + r4^2) + r1*r4^2 - r1*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) + r3^2*r4 - r3^2*sqrt(r1^2 + 6*r1*r4 + r4^2) + r3*r4^2 - r3*r4*sqrt(r1^2 + 6*r1*r4 + r4^2)) + (r1^3*r3^2 - 2*r1^3*r3*r4 + r1^3*r4^2 + r1^2*r3^3 + 6*r1^2*r3^2*r4 - r1^2*r3^2*sqrt(r1^2 + 6*r1*r4 + r4^2) - 10*r1^2*r3*r4^2 + r1^2*r4^3 + r1^2*r4^2*sqrt(r1^2 + 6*r1*r4 + r4^2) + 4*r1*r3^3*r4 - r1*r3^3*sqrt(r1^2 + 6*r1*r4 + r4^2) + 6*r1*r3^2*r4^2 - r1*r3^2*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) - 2*r1*r3*r4^3 + r3^3*r4^2 - r3^3*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) + r3^2*r4^3 - r3^2*r4^2*sqrt(r1^2 + 6*r1*r4 + r4^2))^2)/(4*r1*r4*(r1*r3 - r1*r4 + r3^2 + r3*r4)) + (-r1^3*r3^2 + 2*r1^3*r3*r4 - r1^3*r4^2 - r1^2*r3^3 - 6*r1^2*r3^2*r4 + r1^2*r3^2*sqrt(r1^2 + 6*r1*r4 + r4^2) + 10*r1^2*r3*r4^2 - r1^2*r4^3 - r1^2*r4^2*sqrt(r1^2 + 6*r1*r4 + r4^2) - 4*r1*r3^3*r4 + r1*r3^3*sqrt(r1^2 + 6*r1*r4 + r4^2) - 6*r1*r3^2*r4^2 + r1*r3^2*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) + 2*r1*r3*r4^3 - r3^3*r4^2 + r3^3*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) - r3^2*r4^3 + r3^2*r4^2*sqrt(r1^2 + 6*r1*r4 + r4^2))/(4*r1*r4*(r1*r3 - r1*r4 + r3^2 + r3*r4))

res[4][2] |> println

   (-r1^3*r3^2 + r1^3*r3*r4 - 2*r1^3*r4^2 - r1^2*r3^3 - 5*r1^2*r3^2*r4 + r1^2*r3^2*sqrt(r1^2 + 6*r1*r4 + r4^2) + 2*r1^2*r3*r4^2 + r1^2*r3*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) - 2*r1^2*r4^3 - 2*r1*r3^3*r4 + r1*r3^3*sqrt(r1^2 + 6*r1*r4 + r4^2) - 5*r1*r3^2*r4^2 + 2*r1*r3^2*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) + r1*r3*r4^3 + r1*r3*r4^2*sqrt(r1^2 + 6*r1*r4 + r4^2) - r3^3*r4^2 + r3^3*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) - r3^2*r4^3 + r3^2*r4^2*sqrt(r1^2 + 6*r1*r4 + r4^2))/(8*r1*r4*(r1*r3 - r1*r4 + r3^2 + r3*r4))

res[4][3] |> println

   (3*r1^3*r3 - r1^3*r4 + 9*r1^2*r3*r4 - r1^2*r3*sqrt(r1^2 + 6*r1*r4 + r4^2) + r1^2*r4^2 - r1^2*r4*sqrt(r1^2 + 6*r1*r4 + r4^2) - 3*r1*r3^3 - 7*r1*r3^2*r4 - r3^3*r4 + r3^3*sqrt(r1^2 + 6*r1*r4 + r4^2) - r3^2*r4^2 + r3^2*r4*sqrt(r1^2 + 6*r1*r4 + r4^2))/(8*r1*(r1*r3 - r1*r4 + r3^2 + r3*r4))

res[4][4] |> println
res[4][4](r1 => 5, r3 => 3, r4 => 7.5).evalf() |> println

   -(r1 + r3)*(r3 - r4)*(r3 + r4)*sqrt(r1^2 + 6*r1*r4 + r4^2)/(8*r4*(r1*r3 - r1*r4 + r3^2 + r3*r4)) + (r3 - r4)*(r1^2*r3 + r1^2*r4 + r1*r3^2 + 8*r1*r3*r4 - r1*r4^2 + 3*r3^2*r4 + 3*r3*r4^2)/(8*r4*(r1*r3 - r1*r4 + r3^2 + r3*r4))

res[4][1](r1 => 5, r3 => 3, r4 => 7.5).evalf() |> println
res[4][2](r1 => 5, r3 => 3, r4 => 7.5).evalf() |> println
res[4][3](r1 => 5, r3 => 3, r4 => 7.5).evalf() |> println
res[4][4](r1 => 5, r3 => 3, r4 => 7.5).evalf() |> println

   10.0000000000000
   2.70833333333333
   0.666666666666667
   -1.37500000000000

まえもって r1, r3, r4 に定数を代入しておいてから解くと数値解が求まる。

@syms r0::positive, x0::negative, y0::positive,
     r1::positive, r2::positive, r3::positive, r4::positive
@syms r0, x0, y0, r1, r2, r3, r4
(r1, r3, r4) = (10, 6, 15) .// 2
eq1 = (r1 - x0)^2 + (r1 - y0)^2 - (r0 + r1)^2
eq2 = (r2 - x0)^2 + (-r2 - y0)^2 - (r0 + r2)^2
eq3 = (-r3 - x0)^2 + (r3 - y0)^2 - (r0 + r3)^2
eq4 = (-r4 - x0)^2 + (-r4 - y0)^2 - (r0 + r4)^2
res = solve([eq1, eq2, eq3, eq4], (r2, r0, x0, y0))

   4-element Vector{NTuple{4, Sym{PyCall.PyObject}}}:
    (-18, -305/8, 17, -207/8)
    (55/2, -305/8, 17, -207/8)
    (-1/2, 65/24, 2/3, -11/8)
    (10, 65/24, 2/3, -11/8)

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3, r4) = (10, 6, 15) .// 2
   (r2, r0, x0, y0) = [10, 65/24, 2/3, -11/8]
   plot()
   circle(r1, r1, r1)
   circle(r2, -r2, r2, :blue)
   circle(-r3, r3, r3, :green)
   circle(-r4, -r4, r4, :magenta)
   circle(x0, y0, r0, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
       point(x0, y0, "容円:r0,(x0,y0)", :black, :left, delta=-delta/2)
       point(r1, r1, "坤円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(r2, -r2, "乾円:r2,(r2,-r2)", :blue, :center, delta=-delta/2)
       point(-r3, r3, "巽円:r3\n(-r3,r3)", :green, :center, :bottom, delta=delta/2)
       point(-r4, -r4, "艮円:r4\n(-r4,-r4)", :magenta, :center, :bottom, delta=delta/2)
   end
end;

 

算額（その789）

算額（その789）

藤田貞資門人 東都 八木林平質 文化三年丙寅正月
藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

十四 群馬県佐波郡玉村町樋越 神明宮 文化3年(1806)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.

キーワード：円1個，円弧1個，直角三角形
#Julia, #SymPy, #算額, #和算

直角三角形の中に容円と 2 つの頂点を通る弧が入っている。容円は直角三角形の 2辺と接し，弧とも接している。直角を挟む二辺の短い方（鈎）と長い方（股）の長さがそれぞれ 9 寸，12 寸のとき，容円が最小であるときの直径を求めよ。

少し考えると，容円は大きくなる一方である。最小というのは0ではないが，暗黙のうちに，「弧と容円が図のような配置のとき」という条件がある。つまり，「弧は斜辺と 2 点で交わってはいけない」ということであり，斜辺と1点で交わるときは弧が薄くなっていけば容円は大きくなり続ける。弧が一番厚いのは，斜辺が弧の接線のときである。

鈎，股を a, b
弧がその一部である円の半径と中心座標を r1, (b/2, y1)
容円の半径と中心座標を r2, (r2, y2)
とおく。
斜辺が弧の接線であるということは，(b/2)/y1 = a/b ということである。
以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms a, b, r1::positive, y1::negative, r2::positive, y2::positive, d
(a, b) = (Sym(9), Sym(12))
y1 = -b^2/2a
eq1 = (b/2 - r2)^2 + (y2 - y1)^2 - (r1 + r2)^2
eq2 = b^2/4 + y1^2 - r1^2
eq3 = (sqrt(a^2 + b^2) +a)*r2 + y2*b - a*b
res = solve([eq1, eq2, eq3], (r1, r2, y2))

   1-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (10, 5/2, 4)

鈎，股の長さがそれぞれ 9 寸，12 寸のとき条件を満たすときの容円の直径の最小値は 5 寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (9, 12)
   y1 = -b^2/2a
   (r1, r2, y2) = (10, 5/2, 4)
   plot([0, b, 0, 0], [0, 0, a, 0], color=:black, lw=0.5)
   circle(r2, y2, r2)
   θ = atand(-y1, b/2)
   circle(b/2, y1, r1, :blue, lw=0.2)
   circle(b/2, y1, r1, :blue, beginangle=θ, endangle=180 - θ, lw=1)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(b/2, y1, "(b/2,y1)", :blue, :center, delta=-delta/2)
       point(r2, y2, " 容円:r2,(r2,y2)", :red, :left, :vcenter)
       point(b, 0, " b", :black, :left, :bottom, delta=delta/2)
       point(0, a, " a", :black, :left, :bottom, delta=delta/2)
       plot!(ylims=(1.15y1, 10))
   end
end;

算額（その788）

算額（その788）

享和3年癸亥五月 丸山良玄門人 豫州松山 大西佐兵衛義全
藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

平田浩一：愛媛の和算と算額，日本数学会秋季総合分科会市民講演会，2013/9/23.
https://www.mathsoc.jp/publication/tushin/1804/1804hirata.pdf

弧環減球に中球 2 個と小球 1 個を除いた体積を求めよ。

弧環減球は円を両側から 2 円でくり抜き，それを回転させて得られる回転体である。図の太い黒で示した図形を y 軸を中心として回転する。上の図は，それを三次元表示したものである。

曲線が切り替わる点 (x0, y0) を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms R, r1, r2, r3, x0, y0
(r2, r3) = (3, 2) .// 2
R = 2r2 + r3
eq1 = (r1 + r3)^2 + (r3 + r2)^2 - (r1 + r2)^2
eq2 = (x0 - r1 - r3)^2 + y0^2 - r1^2
eq3 = x0^2 + y0^2 - R^2
res = solve((eq1, eq2, eq3), (r1, x0, y0))

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (5, 9/4, -5*sqrt(7)/4)
    (5, 9/4, 5*sqrt(7)/4)

[0, 5√7/4] で回転体の体積 res1 を求める。

@syms x
res1= integrate(PI*(-sqrt(25 - x^2) + 6)^2, (x, 0, res[2][3]))
res1 |> println
res1.evalf() |> println

   pi*(-150*asin(sqrt(7)/4) + 8365*sqrt(7)/192)
   21.5487629153420

[5√7/4, 4]で回転体の体積 res2 を求める。

res2 = integrate(PI*sqrt(16 - x^2)^2, (x, res[2][3], 4))
res2 |> println
res2.evalf() |> println

   -2965*sqrt(7)*pi/192 + 128*pi/3
   5.68345793167528

3 個の球の体積の和 res3 を求める。

res3 = 4PI/3*(2*(3//2)^3 + (2//2)^3)
res3 |> println
res3.evalf() |> println

   31*pi/3
   32.4631240870945

求める立体の体積 res を求める。

res = 2res1 + 2res2 - res3 
res |> println
res |> simplify |> println
res.evalf() |> println

   -2965*sqrt(7)*pi/96 + 2*pi*(-150*asin(sqrt(7)/4) + 8365*sqrt(7)/192) + 75*pi
   75*pi*(-16*asin(sqrt(7)/4) + 4 + 3*sqrt(7))/4
   22.0013176069401

求める体積は，75π(4 + 3√7 - 16asin(√7/4))/4 = 22.001317606940137 である。

75π*(4 + 3√7 - 16asin(√7/4))/4

   22.001317606940137

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3) = (3, 2) .// 2
   r1 = 5
   R = 2r2 + r3
   println("R = $R")
   (r1, x0, y0) = (5, 9/4, 5*sqrt(7)/4)
   θ1 = atand(y0, x0)
   θ2 = atand(y0, r1 + r3 - x0)
   plot()
   circle(0, 0, R, :palevioletred1)
   circle(0, 0, R, :black, beginangle=θ1, endangle=90, lw=2)
   circle(0, 0, R, :black, beginangle=270, endangle=360-θ1, lw=2)
   circle22(0, r3 + r2, r2, :magenta)
   circle(0, 0, r3, :orange)
   circle(r1 + r3, 0, r1, :blue)
   circle(r1 + r3, 0, r1, :black, beginangle=180-θ2, endangle=180+θ2, lw=2)
   segment(0, r3 + 2r2, 0, -r3 - 2r2, :black, lw=2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1 + r3, 0, "r1+r3")
       point(0, r3, " r3", :black, :left, :bottom, delta=delta)
       point(0, r3+ r2, " r3+r2", :magenta, :left, :vcenter)
       point(x0, y0, " (x0,y0)", :black, :left, :vcenter, mark=false)
   end
end;