算額（その787）

算額（その787）

寛政十年戊午九月(1798) 藤田貞資門人 肥後人吉 西九郎左衛門孟周
藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

正方形内に円弧（弧背）と等円 3 個を入れる。正方形の一辺の長さが 971 寸のとき，等円の直径はいかほどか。

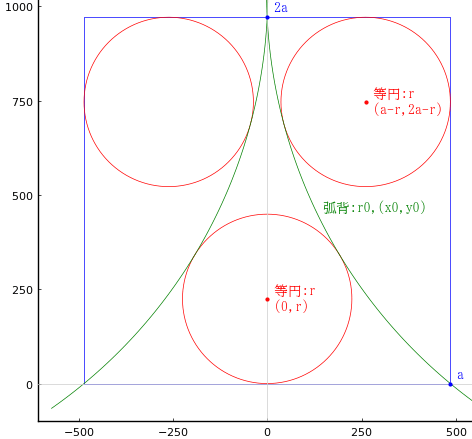
最初に見たとき，正方形の上辺で 2 つの円弧は互いに外接しているかと思ったが，そうではなかった。そこで交わっている。

正方形の一辺の長さを 2a
等円の半径と中心座標を r, (0, r), (a - r, 2a - r)
円弧のもとの円の半径と中心座標を r0, (x0, y0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms r0::positive, x0::positive, y0::positive, a::positive, r::positive
#a = 971//2
eq1 = (x0 - (a - r))^2 + (y0 - (2a - r))^2 - (r0 - r)^2
eq2 = x0^2 + (y0 - r)^2 - (r0 + r)^2
eq3 = (x0 - a)^2 + y0^2 - r0^2
eq4 = x0^2 + (y0 - 2a)^2 - r0^2;
res = solve([eq1, eq2, eq3, eq4], (r, r0, x0, y0))

   1-element Vector{NTuple{4, Sym{PyCall.PyObject}}}:
    (a*(-5*sqrt(5) + sqrt(14 + 10*sqrt(5)) + 7)/4, 5*a*(-34 - 14*sqrt(5) + 5*sqrt(70 + 50*sqrt(5)) + 13*sqrt(14 + 10*sqrt(5)))/(8*(-sqrt(2)*sqrt(7 + 5*sqrt(5)) + 5*sqrt(5) + 13)), a*(-sqrt(14 + 10*sqrt(5)) + 5*sqrt(5) + 17)/8, a*(-sqrt(7/128 + 5*sqrt(5)/128) + 5*sqrt(5)/16 + 29/16))

等円の直径は，正方形の一辺の長さの (sqrt(14 + 10*√5) + 7 - 5√5)/4 倍である。

正方形の一辺の長さが 971 寸のとき，等円の直径は 449.00055949866737 寸である。

数式はそんなに長くないと思うが，術は結構長い。

971*(sqrt(14 + 10*√5) + 7 - 5√5)/4

   449.00055949866737

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 971//2
   (r, r0, x0, y0) = (a*(-5*sqrt(5) + sqrt(14 + 10*sqrt(5)) + 7)/4, 5*a*(-34 - 14*sqrt(5) + 5*sqrt(70 + 50*sqrt(5)) + 13*sqrt(14 + 10*sqrt(5)))/(8*(-sqrt(2)*sqrt(7 + 5*sqrt(5)) + 5*sqrt(5) + 13)), a*(-sqrt(14 + 10*sqrt(5)) + 5*sqrt(5) + 17)/8, a*(-sqrt(7/128 + 5*sqrt(5)/128) + 5*sqrt(5)/16 + 29/16))
   @printf("等円の直径 = %g;  r = %g;  r0 = %g;  x0 = %g\n", 2r, r, r0, x0)
   plot([a, a, -a, -a, a], [0, 2a, 2a, 0, 0], color=:blue, lw=0.5)
   circle2(a - r, 2a - r, r)
   circle(0, r, r)
   circle(x0, y0, r0, :green, beginangle=180, endangle= 235)
   circle(-x0, y0, r0, :green, beginangle=305, endangle= 360)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r, " 等円:r\n (0,r)", :red, :left, :vcenter)
       point(a - r, 2a - r, " 等円:r\n (a-r,2a-r)", :red, :left, :vcenter)
       point(0, 2a, " 2a", :blue, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0.3a, a, "弧背:r0,(x0,y0)", :green, :left, mark=false)
   end
end;

 

算額（その786）

算額（その786）

福島県白河市南湖 南湖神社 昭和58年(1983)
http://www.wasan.jp/fukusima/nanko.html

外円の中に大小の正方形と甲乙丙の 3 円が入っている（甲円ははみ出すが）。丙円の直径がわかっているとき，外円の直径を求めよ。

それぞれの図形が独立なので，上から順に図形を構成していく。

外円の半径と中心座標を R, (0, 0)，大正方形の一辺の長さを a とする。
右にある大正方形の右上の頂点座標から，以下の方程式を解くことにより a が決定される。

include("julia-source.txt");

@syms R, a
eq = sqrt(R^2 - (R - a)^2) - 2a;
solve(eq, a)

   2-element Vector{Sym{PyCall.PyObject}}:
        0
    2*R/5

斜線と外円の交点座標 (x02, y02) を求める。傾きは -1 である。

@syms x02, y02
a = 2R/5
eq1 = (R - a - y02)/x02 + 1
eq2 = x02^2 + y02^2 - R^2;
solve([eq1, eq2], (x02, y02))

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (R*(-3 + sqrt(41))/10, R*(3 + sqrt(41))/10)
    (R*(-sqrt(41) - 3)/10, R*(3 - sqrt(41))/10)

@syms r1, r2, r3
(x02, y02) = (R*(sqrt(Sym(41)) + 3)/10, R*(3 - sqrt(Sym(41)))/10)
eq3 = distance(0, R - a, x02, y02, r2, R - 2a - r2) - r2^2
eq4 = distance(0, R - a, x02, y02, 2r1, R - 2a - 2r2 - r1) - r1^2
eq5 = r1^2 + (r1 - r3)^2 - (r1 + r3)^2
solve([eq3, eq4, eq5], (r1, r2, r3))

   4-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (2*R/5, -sqrt(2)*R/5, R/10)
    (2*R/5, sqrt(2)*R/5, R/10)
    (2*R*(-3 - 2*sqrt(2))/5, sqrt(2)*R/5, R*(-3/10 - sqrt(2)/5))
    (2*R*(-3 + 2*sqrt(2))/5, -sqrt(2)*R/5, R*(-3/10 + sqrt(2)/5))

2番目のものが適解である。

甲円，乙円，丙円の半径はそれぞれ，外円の半径の，2/5, √2/5, 1/10 倍である。

例えば，外円の直径が 10 寸のとき，乙円の半径は 1 寸である。

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 5
   (a, r1, r2, r3) = R .* (2/5, 2/5, √2/5, 1/10)
   @printf("丙円の直径 = %g;  外円の直径 = %g;  甲円の直径 = %g;  乙円の直径 = %g\n", 2r3, 2R, 2r1, 2r2)
   @printf("R = %g;  r1 = %g;  r2 = %g;  r3 = %g\n", R, r1, r2, r3)
   y01 = R - a
   x01 = sqrt(R^2 - y01^2)
   plot([0, a/2, 0, -a/2, 0, 0, a/2, 0, -a/2, 0],
       [R - a, R - a/2, R, R - a/2, R - a, R - 2a, R - 3a/2, R - a, R - 3a/2, R - 2a],
       color=:black, lw=0.5)
   rect(x01, y01, x01 - a, y01 - a, :black)
   rect(x01 - 2a, y01, x01 - a, y01 - a, :black)
   rect(-x01, y01, -x01 + a, y01 - a, :black)
   rect(-x01 + 2a, y01, -x01 + a, y01 - a, :black)
   circle(0, 0, R)
   circle2(r2, R - 2a - r2, r2, :blue)
   circle(0, R - 2a - 2r2 - r1, r1, :green)
   circle2(2r1, R - 2a - 2r2 - r1, r1, :green)
   circle2(r1, R - 2a - 2r2 - r3, r3)
   factor = 5R/4
   segment(-factor, R - 2a - 2r2, factor, R - 2a - 2r2, :orange)
   segment(0, R - a, factor, R - a - factor, :orange)
   segment(0, R - a, -factor, R - a - factor, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(2r1, R - 2a - 2r2 - r1, "甲円：r1,(r2,R-2a-r1)", :black, :center, delta=-delta/2)
       point(r2, R - 2a - r2, "乙円：r2,(r2,R-2a-r2)", :black, :center, delta=-delta/2)
       point(r1, R - 2a - 2r2 - r3, "丙円：r3,(r2,R-2a-2r2-r3)", :red, :center, delta=-delta/2)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(0, R - a, "  R-a", :green, :left, :bottom, delta=delta/2)
       point(0, R - 2a, "  R-2a", :green, :left, :bottom, delta=delta/2)
       point(2a, R - a, "(2a,R-a) ", :black, :right, :bottom, delta=delta/2)
   end
end;