算額(その792)
文化元年甲子九月 藤田貞資門人 北越村上藩 杉村勘助道定
藤田嘉言(1807):続神壁算法
http://www.wasan.jp/jinpeki/jinpeki.html
圓壔(えんとう;円柱)から弧環(トーラス?)で欠き取った鼓状の物体内に大球 2 個と,数個の小球が入っている。小球は大球と外側面および両隣の小球に接する(小球間の隙間はない)。円柱の底面(円)の直径が 35 寸 9 分のとき,円柱の高さはいかほどか。
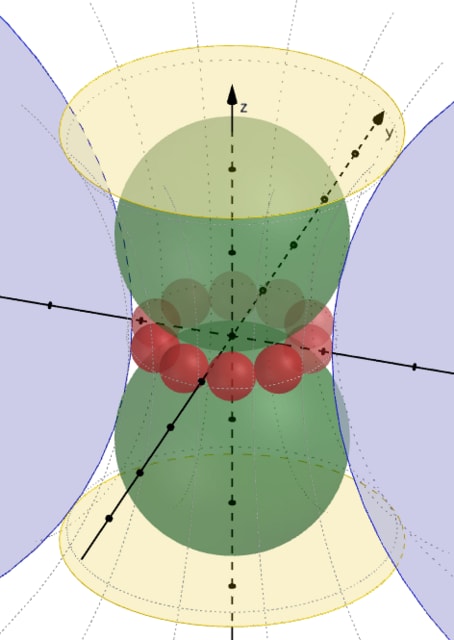
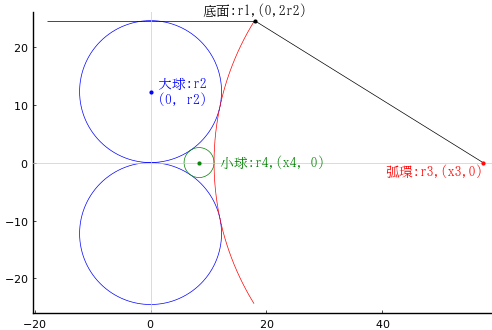
円柱の高さ,底面の半径と中心座標を 4r2, r1, (0, 0, 2r2)
大球の半径と中心座標を r2, (0, 0, r2)
小球の半径と中心座標を r4, (x4, 0, 0)
とおき,以下の連立方程式を解くが,小球の個数を試行錯誤で決める必要がある(?)。
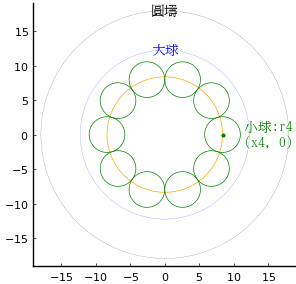
n = 10 のときに,条件を満たす解が得られた。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms r1::positive, r2::positive, r3::positive,
x3::positive, r4::positive, x4::positive,
h::positive, n::integer
h = 2r2
n = 10
eq1 = x3^2 + r2^2 - (r2 + r3)^2
eq2 = (x3 - r1)^2 + h^2 - r3^2
eq3 = x4^2 + r2^2 - (r2 + r4)^2
eq4 = x4 + r4 + r3 - x3
eq5 = x4*sind(Sym(180)//n) - r4
res = solve((eq1, eq2, eq3, eq4, eq5), (r2, r3, x3, r4, x4));
2 組の解が得られるが,2 番目のものが適解である。
res[2][1] |> println
res[2][4] |> println
res[2][5] |> println
r1*(29*sqrt(5 + 5*sqrt(5)) + 65*sqrt(1 + sqrt(5)) + 125 + 56*sqrt(5))/(2*(40*sqrt(1 + sqrt(5)) + 18*sqrt(5)*sqrt(1 + sqrt(5)) + 105 + 47*sqrt(5)))
-3*sqrt(5)*r1*sqrt(5 + 5*sqrt(5))/5 - sqrt(5)*r1*sqrt(1 + sqrt(5)) - r1/4 + 3*sqrt(5)*r1/20 + 9*r1*sqrt(1 + sqrt(5))/4 + 27*r1*sqrt(5 + 5*sqrt(5))/20
-sqrt(5)*r1/10 + r1*sqrt(1 + sqrt(5))/(2*sqrt(5) + 5) + r1/2
円柱の底面(円)の直径が 35 寸 9 分のとき,円柱の高さは 49.0003 寸,小球の個数は 10 個で,小球の半径は 2.58655 寸,小球の中心を通る円の半径は 8.37025 寸である。
その他のパラメータは以下のとおりである。
r2 = 12.2501; r3 = 46.4137; x3 = 57.3705; r4 = 2.58655; x4 = 8.37025
function draw(more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = 35.9/2
u = √5
t = sqrt(1 + u)
s = u*t
(r2, r3, x3, r4, x4) = (
359(29s + 65t + 125 + 56u)/(40(18s + 40t + 47u + 105)),
359(30254s + 67650t + 58301u + 130365)/(200(987s + 2207t + 2584u + 5778)),
359(987s + 2207t + 4253 + 1902u)/(10(521s + 1165t + 1364u + 3050)),
(2513s -5385t + 1077u - 1795)/400,
-359u/200 + 359t/(20(2u + 5)) + 359/40)
h = 2r2
n = 10
@printf("円柱の高さ = %g; 小球の個数 = %g; 小球の半径 = %g\n", 4r2, n, r4)
@printf("r2 = %g; r3 = %g; x3 = %g; r4 = %g; x4 = %g\n", r2, r3, x3, r4, x4)
θ = atand(h, x3 - r1)
plot()
circle22(0, r2, r2, :blue)
circle(x3, 0, r3, beginangle=180 - θ, endangle=180 + θ)
circle(x4, 0, r4, :green)
segment(-r1, h, r1, h, :black)
segment(r1, h, x3, 0)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, r2, " 大球:r2\n (0, r2)", :blue, :left, :vcenter)
point(x4, 0, " 小球:r4,(x4, 0)", :green, :left, :vcenter)
point(r1, h, "底面:r1,(0,2r2)", :black, :center, :bottom, delta=delta)
point(x3, 0, "弧環:r3,(x3,0)", :red, :right, delta=-delta/2)
end
function rotate2(ox, oy, r, color=:red; angle=120, beginangle=0, endangle=360, by=0.5, n=0)
for deg in 0:angle:360-1
(ox2, oy2) = [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * [ox; oy]
@printf("(x-%g)^2+(y-%g)^2+z^2=%g^2\n", ox2, oy2, r)
circle(ox2, oy2, r, color; beginangle, endangle, by, n)
beginangle += angle
endangle += angle
end
end;
pyplot(size=(300, 300), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
plot()
circle(0, 0, r1, :black, lw=0.1)
circle(0, 0, r2, :blue, lw=0.1)
circle(0, 0, x4, :orange)
rotate2(x4, 0, r4, :green, angle=2*18)
point(x4, 0, " 小球:r4\n (x4, 0)", :green, :left, :vcenter)
point(0, r1, "圓壔", :black, :center, :vcenter, mark=false)
point(0, r2, "大球", :blue, :center, :vcenter, mark=false)
end;


















