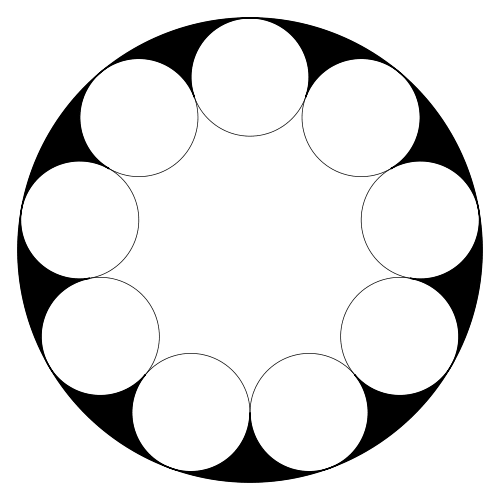
算額（その815）

算額（その815）

藤田貞資：精要算法（下巻），天明元年(1781)
http://www.wasan.jp/seiyou/seiyou.html

大円内に 5 個の等円を描く。外円と等円の直径をそれぞれ 16 寸，10 寸としたとき，5 個の円の共通部分（黒積）を求めよ。

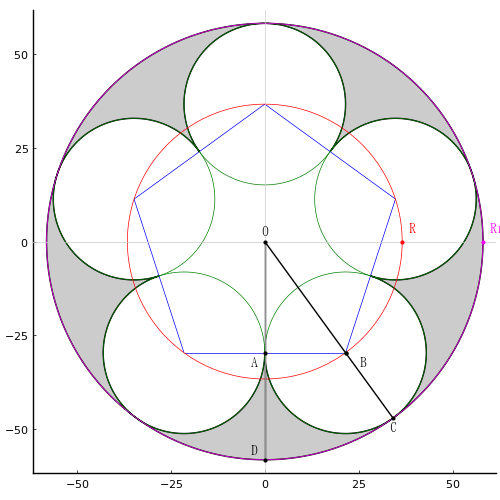
求めたい面積 S は
S1 = B を中心とする半径 r1 の円の ∠CBE/360 倍
S2 = 三角形 BCE
S3 = 三角形 OCE
とすると，
S = S1 - S2 + S3

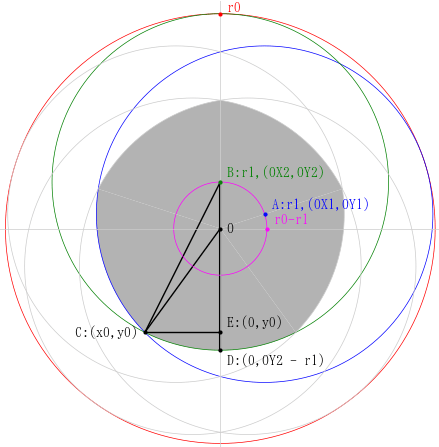
まず，2個の等円の交点座標 C:(x0, y0) を求める。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r0, r1, R, x0, y0, OX1, OY1, OX2, OY2
R = r0 - r1
(OX1, OY1) = (R*cosd(Sym(18)), R*sind(Sym(18)))
(OX2, OY2) = (0, R)
eq1 = (x0 - OX1)^2 + (y0 - OY1)^2 - r1^2
eq2 = (x0 - OX2)^2 + (y0 - OY2)^2 - r1^2
res = solve([eq1, eq2], (x0, y0));

x0 = res[2][1] |> factor
y0 = res[2][2] |> factor;

角度 ∠COE を求める

θ = asind(-x0/r1);

S1, S2, S3 を求める。式は長いが，そのままにしておく。

S1 = π*r1^2*θ/360
S2 = (-x0)*(OY2 - y0)/2
S3 = x0*y0/2
S1 |> println
S2 |> println
S3 |> println

   -r1^2*asin((-5*sqrt(2) + sqrt(10))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(8*r1*(-5 + sqrt(5))*sqrt(sqrt(5) + 5)))/2
   -(-5*sqrt(2) + sqrt(10))*(r0 - r1 + (sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(4*(-5 + sqrt(5))))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(16*(-5 + sqrt(5))*sqrt(sqrt(5) + 5))
   -(-5*sqrt(2) + sqrt(10))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))^2/(64*(-5 + sqrt(5))^2*sqrt(sqrt(5) + 5))

面積を求める。

S = 10(S1 - S2 + S3)
S |> println

   -5*r1^2*asin((-5*sqrt(2) + sqrt(10))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(8*r1*(-5 + sqrt(5))*sqrt(sqrt(5) + 5))) + 5*(-5*sqrt(2) + sqrt(10))*(r0 - r1 + (sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(4*(-5 + sqrt(5))))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(8*(-5 + sqrt(5))*sqrt(sqrt(5) + 5)) - 5*(-5*sqrt(2) + sqrt(10))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))^2/(32*(-5 + sqrt(5))^2*sqrt(sqrt(5) + 5))

r0 = 16//2, r1 = 10//2 を代入して数値を求める。
面積は 13.6341847764931 平方寸（歩）である。

S(r0 => 16//2, r1 => 10//2).evalf() |> println

   13.6341847764931

S(r0 => 1872//2, r1 => 1466//2).evalf() |> println

   915183.000045518

function transform(x, y; deg=0, dx=0, dy=0)
  return [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * [x, y]
end;

function rotatefigure(x2, y2)
   for i in 1:5
       plot!(x2, y2, seriestype=:shape, color=:gray70, fillcolor=:gray70, lw=0)
       i == 5 && return
       (x2, y2) = transform(x2, y2, deg = 72)
   end
end;

function fillblack(r1, θ, OX2, OY2)
   x2 = []
   y2 = []
   for i in 270 - θ:0.5:270
       append!(x2, r1*cosd(i) + OX2)
       append!(y2, r1*sind(i) + OY2)
   end
   x2 = vcat(x2, -reverse(x2), [0, x2[1]])
   y2 = vcat(y2,  reverse(y2), [0, y2[1]])
   rotatefigure(x2, y2)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   x = Vector{Float64}(undef, 6)
   y = Vector{Float64}(undef, 6)
   (r0, r1) = (16, 10) .// 2
   (r0, r1) = (1872, 1466) .// 2
   R = r0 - r1
   for i = 1:6
       θ = 18 + (i - 1)*72
       x[i] = R*cosd(θ)
       y[i] = R*sind(θ)
   end
   (OX1, OY1) = (R*cosd(18), R*sind(18))
   (OX2, OY2) = (0, R)
   x0 = (-5*sqrt(2) + sqrt(10))*(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(8*(-5 + sqrt(5))*sqrt(sqrt(5) + 5))
   y0 = -(sqrt(5)*r0 + 5*r0 - 5*r1 - sqrt(5)*r1 - sqrt(10)*sqrt(-5*r0^2 + sqrt(5)*r0^2 - 2*sqrt(5)*r0*r1 + 10*r0*r1 + sqrt(5)*r1^2 + 3*r1^2))/(4*(-5 + sqrt(5)))
   θ = asind(-x0/r1)
   println("θ = $θ")
   S = 10(π*r1^2*θ/360 - (-x0)*(OY2 - y0)/2 + x0*y0/2)
   println("S = $S")
   plot()
   fillblack(r1, θ, OX2, OY2)
   segment(OX2, OY2, x0, y0, :black, lw=1)
   segment(OX2, OY2, 0, OY2 - r1, :black, lw=1.5)
   segment(0, y0, x0, y0, :black, lw=1)
   segment(0, 0, x0, y0, :black, lw=1)
   circle(0, 0, r0)
   circle(0, 0, r0 - r1, :magenta)
   color = [:blue, :green, :gray80, :gray80, :gray80]
   for i = 1:5
       # segment(x[i], y[i], x[i + 1], y[i + 1], :blue)
       circle(x[i], y[i], r1, color[i])
   end
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(OX1, OY1, " A:r1,(OX1,OY1)", :blue, :left, :bottom, delta=delta/2)
       point(OX2, OY2, " B:r1,(OX2,OY2)", :green, :left, :bottom, delta=delta/2)
       point(x0, y0, "C:(x0,y0) ", :black, :right, :vcenter)
       point(0, OY2 - r1, " D:(0,OY2 - r1) ", :black, :left, delta=-delta/2)
       point(0, y0, " E:(0,y0) ", :black, :left, :bottom, delta=delta/2)
       point(0, 0, " O", :black, :left, :vcenter)
       point(r0 - r1, 0, " r0-r1", :magenta, :left, :bottom, delta=delta/2)
       point(0, r0, " r0", :red, :left, :bottom)
       # plot!(xlims=(-3, 5), ylims=(-3, 3))
   end
end;

   θ = 26.63149441418678
   S = 915183.0000455183

r0，r1 を与えて黒積を返す関数を定義する。

function func(r0, r1)
   p = √5 + 5
   q = √5 - 5
   s = p*(r0 - r1) - √10*sqrt(q*r0*(r0 - 2r1) + r1^2*(√5 + 3))
   t = (√10 - 5√2)*s/(8q√p)
   5(r0*t - r1*t - r1^2*asin(t/r1))
end;
func(8, 5)

   13.634184776493093

この関数を使って，黒積が整数に極めて近い値になるときの r0, r1 の組を探索することもできる。
そのような候補として，r0 = 1872/2, r1 = 1466/2 のとき，黒積が 915183.0000455179 になる。

func(936, 733)

   915183.0000455179

 

算額・和算の挑戦状

精要算法（下巻）にもある問題で，算法助術にも助術用例3として解説されているものである。

そこでは，等円が5個の場合を取り上げている。

これを一般化して，外円内に n  個の等円を入れる。外円と等円に挟まれる部分の面積（黒積）が与えられたとき，等円の直径を求めよ。

n = 9, 黒積 = 66522.03 のとき，等円の直径はいかほどか...

 

算額（その814）

算額（その814）

藤田貞資：精要算法（下巻），天明元年(1781)
http://www.wasan.jp/seiyou/seiyou.html

外円内に 5 個の等円を入れる。外円と等円に挟まれる部分の面積（黒積）が 2330.89 歩のとき，等円の直径を求めよ。

黒積は，「扇形 OCD - 直角三角形 OAB - 扇形ACB」の面積の 10 倍である。
等円の半径 OB = R，AB = r とすれば，∠AOB = 36° より，R = r/sind(36)
OC = OB + BC = R + r = Rr とすれば，
扇形 OCD = πRr^2/10
直角三角形 OAB = r*R*cosd(36)/2
扇形 ACB = πr^2*(126/360)
よって，黒積 = 10*(π*Rr^2/10 - r*R*cosd(36)/2 - π*r^2*126/360)
黒積 = 2332.89 を解いて r を求めると，r = 21.5000025771553，等円の直径は 43.0000051543107 寸である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r::positive, R::positive, Rr::positive,
     黒積::positive, BLK::positive

R = solve(R*sind(Sym(36)) - r, R)[1]
Rr = R + r
R |> println
Rr |> println
(R.evalf(), Rr.evalf()) |> println

   2*sqrt(2)*r/sqrt(5 - sqrt(5))
   r + 2*sqrt(2)*r/sqrt(5 - sqrt(5))
   (1.70130161670408*r, 2.70130161670408*r)

黒積 = PI*Rr^2/10 - R*r*cosd(Sym(36))/2 - PI*r^2*126//360
eq = 10黒積 - BLK  # 2332.89;
eq |> println

   -BLK - 7*pi*r^2/2 - 10*sqrt(2)*r^2*(1/4 + sqrt(5)/4)/sqrt(5 - sqrt(5)) + pi*(r + 2*sqrt(2)*r/sqrt(5 - sqrt(5)))^2

方程式を解いて，等円の直径を求める。

res = 2solve(eq, r)[1]
res |> println

   2*sqrt(2)*sqrt(BLK)*(5 - sqrt(5))^(3/4)/sqrt(-8*sqrt(10)*pi - 20*sqrt(10) - 9*pi*sqrt(5 - sqrt(5)) + 5*sqrt(5)*pi*sqrt(5 - sqrt(5)) + 40*sqrt(2)*pi)

黒積が 2332.89 のときの等円の直径を求める。

res(BLK => 2332.89) |> println

   96.6*sqrt(2)*(5 - sqrt(5))^(3/4)/sqrt(-8*sqrt(10)*pi - 20*sqrt(10) - 9*pi*sqrt(5 - sqrt(5)) + 5*sqrt(5)*pi*sqrt(5 - sqrt(5)) + 40*sqrt(2)*pi)

等円の直径は 43 寸である。

res(BLK => 2332.89).evalf() |> println

   43.0000051543107

function transform(x, y; deg=0, dx=0, dy=0)
  return [cosd(deg) -sind(deg); sind(deg) cosd(deg)] * [x, y]
end;

function rotatefigure(x2, y2)
   for i in 1:5
       plot!(x2, y2, color=:gray80, seriestype=:shape, fillcolor=:gray80)
       i == 5 && return
       (x2, y2) = transform(x2, y2, deg = 72)
   end
end;

function fillblack(r, Rr, x, y)
   x2 = []
   y2 = []
   for i in 180:0.5:306
       append!(x2, r*cosd(i) + x[1])
       append!(y2, r*sind(i) + y[1])
   end
   for i in 306:-0.5:270
       append!(x2, Rr*cosd(i))
       append!(y2, Rr*sind(i))
   end
   x2 = vcat(x2, -reverse(x2))
   y2 = vcat(y2, reverse(y2))
   rotatefigure(x2, y2)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   x = Vector{Float64}(undef, 6)
   y = Vector{Float64}(undef, 6)
   r = 21.5000025771553
   R = 2√2*r/sqrt(5 - √5)
   Rr = R + r
   blk = 10(π*Rr^2/10 - R*r*cosd(36)/2 - π*r^2*126/360)
   @printf("等円の直径 = %g;  黒積 = %g;  R = %g;  Rr = %g\n", 2r, blk, R, Rr)
   for i = 1:6
       θ = 306 + (i - 1)*72
       x[i] = R*cosd(θ)
       y[i] = R*sind(θ)
   end
   plot()
   fillblack(r, Rr, x, y)
   for i = 1:5
       segment(x[i], y[i], x[i + 1], y[i + 1], :blue)
       circle(x[i], y[i], r, :green)
   end
   circle(0, 0, R)
   circle(0, 0, Rr, :magenta)
   segment(0, 0, 0, -Rr, :black, lw=1)
   segment(0, 0, Rr*cosd(306), Rr*sind(306), :black, lw=1)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x[1], y[1])
       point(R, 0, " R", :red, :left, :bottom, delta=delta)
       point(Rr, 0, " Rr", :magenta, :left, :bottom, delta=delta)
       point(0, -R*cosd(36), "A ", :black, :right, delta=-delta/2)
       point(x[1], y[1], "  B", :black, :left, delta=-delta/2)
       point(Rr*cosd(306), Rr*sind(306), "C", :black, :center, delta=-delta/2)
       point(0, -Rr, "D ", :black, :right, :bottom, delta=delta/2)
       point(0, 0, "O", :black, :center, :bottom, delta=delta/2)
   end
end;