算額(その1088)
四十一 岩手県一関市牧沢 牧沢八幡神社 明治8年(1875)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:円6個,外円,正五角形,五芒星
正五角形の対角線を引き,区画された領域に甲円 1 個,乙円 5 個を容れる。乙円の直径が 4 寸のとき,甲円の直径はいかほどか。
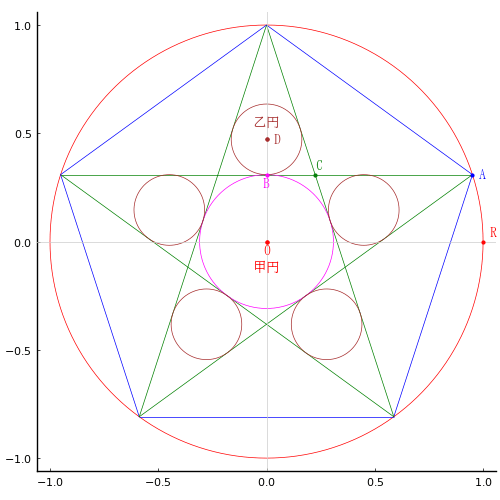
正五角形が内接する円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, 0)
乙円の半径と中心座標を r2, (0, r1 + r2)
とし,以下のように逐次決定してゆく。
計算において,必要な角度がいくつか出てくる。その三角関数の値は無理数ではあるが,きれいな形で表現される。
include("julia-source.txt")
using SymPy
@syms R
s18 = Sym(18)
s36 = Sym(36);
1. 甲円の半径
甲円の半径 OB は五芒星の頂点(正五角形の頂点) A の y 座標値に等しい。
∠AOR は 18° である。
甲円の半径は R*(√5 - 1)/4 である。
r1 = y = R*sind(s18)
r1 |> println
R*(-1/4 + sqrt(5)/4)
2. 乙円の半径
乙円の半径 BD は BC * tan(∠BCD) である。
BC は OB * tan(∠BOC) である。
ここで,∠BCD = ∠BOC = 36°である。
まとめると,乙円の半径は R*(7√5 - 15)/4 である。
OB = R*sind(s18)
r2 = OB*tand(s36)*tand(s36)
r2 |> simplify |> println
R*(-15 + 7*sqrt(5))/4
3. 乙円の直径が既知のときの甲円の直径
甲円の直径は乙円の直径の r1/r2 = 1/(5 - 2√5) = 2√5/5 + 1 = 1.894427190999916 倍である。
乙円の直径が 4 寸のとき,甲円の直径は 7.577708763999664 寸である。
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 1
# r1 = OB = R*sind(18)
# r2 = BD = OB*tand(36)*tand(36)
r1 = R*(√5 - 1)/4
r2 = R*(7√5 - 15)/4
θ = 90:-72:-342
x = R .* cosd.(θ)
y = R .* sind.(θ)
plot()
circle(0, 0, R)
for i in 1:5
segment(x[i], y[i], x[i + 1], y[i + 1], :blue)
segment(x[i], y[i], x[i + 2], y[i + 2], :green)
end
circle(0, 0, r1, :magenta)
rotate(0, r1 + r2, r2, :brown, angle=72)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
point(0, r1, "B", :magenta, :center, delta=-delta/2)
point(0, r1 + r2, " D", :brown, :left, :vcenter)
point(0, r1 + r2, "乙円", :brown, :center, delta=4delta)
point(0, 0, "O", :red, :center, delta=-delta/2)
point(0, 0, "甲円", :red, :center, delta=-3delta)
point(r1*tand(36), r1, "C", :green, :left, :bottom, delta=delta/2)
point(R*cosd(18), r1, " A", :blue, :left, :vcenter)
end
end;


















