算額（その1101）

算額（その1101）

六十六 岩手県花泉町金沢字大柳 金沢八幡宮 明治29年(1896)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，四分円3個，外円

全円の中に 四分円を 3 個，等円を 3 個容れる。正三角形の一辺の長さ（四分円の半径）が与えられたとき，等円の直径を求めよ。

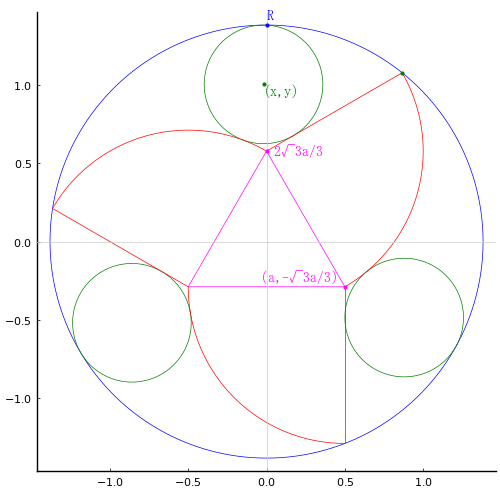
全円の半径と中心座標を R, (0, 0); R = sqrt((√3a/3 + 2a)^2 + a^2) = 2a*sqrt(3√3 + 12)/3
四分円の半径と中心座標を 2a, (0, 2√3a/3), (-a, -√3a/3)
等円の半径と中心座標を r, (x, y); x < 0
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms R::positive, a::positive,
     x::negative, y::positive, r::positive
R = sqrt((√Sym(3)a/3 + 2a)^2 + a^2)
eq1 = (x + a)^2 + (y + √Sym(3)a/3)^2 - (2a + r)^2
eq2 = x^2 + y^2 - (R - r)^2
eq3 = dist2(0, 2√Sym(3)a/3, √Sym(3)a, 2√Sym(3)a/3 + a, x, y, r);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r, x, y) = u
   return [
       (a + x)^2 - (2*a + r)^2 + (sqrt(3)*a/3 + y)^2,  # eq1
       x^2 + y^2 - (-r + sqrt(a^2 + (sqrt(3)*a/3 + 2*a)^2))^2,  # eq2
       a^2 + a*x - sqrt(3)*a*y - r^2 + x^2/4 - sqrt(3)*x*y/2 + 3*y^2/4,  # eq3
   ]
end;
a = 1/2
iniv = BigFloat[0.38, -0.019, 1]
res = nls(H, ini=iniv)

   ([0.3786461241150318, -0.019277088702774222, 1.0034435202087308], true)

正三角形の一辺の長さが 1 のとき，等円の直径は 2*0.3786461241150318 = 0.7572922482300636 である。
算額の「術」は正しいが，山村の解説は途中で数値の参照ミスをしているため結果がだめになっている。「0.636×三角面」ではなく「（正確に）0.7572922482300636×三角面」である。

三角面 = 1
天 = √3
地 = √(天 + 4) + 天
誤 A = sqrt((3*0.732 + 1)*(2地 + 1) + 3) + (地 + 1) 0.732 ではなく 1.732(=√3）
A = sqrt((3天 + 1)*(2地 + 1) + 3) + (地 + 1)
等円径 = A/地^2*三角面

   0.7572922482300636

その他のパラメータは以下のとおりである。

   a = 0.5;  R = 1.38227;  r = 0.378646;  x = -0.0192771;  y = 1.00344

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1/2 #10√3/2
   (r, x, y) = res[1]
   #a = 8.66025;  R = 23.9417;  r = 6.61269;  x = -0.39708;  y = 17.3766
   R = sqrt((√3a/3 + 2a)^2 + a^2)
   @printf("正三角形の一辺の長さが %g のとき，等円の直径は %.15g である。\n", 2a, 2r)
   @printf("a = %g;  R = %g;  r = %g;  x = %g;  y = %g\n", a, R, r, x, y)
   plot([a, 0, -a, a], [-√3a/3, 2√3a/3, -√3a/3, -√3a/3], color=:magenta, lw=0.5)
   circle(0, 0, R, :blue)
   rotate(x, y, r, :green)
   for i = 0:2 # 90:120:330
       ox = 2√3a/3*cosd(90 + 120i)
       oy = 2√3a/3*sind(90 + 120i)
       ba = -60 + 120i
       ea = -60 + 120i + 90
       circle(ox, oy, 2a, beginangle=ba, endangle=ea)
       x1 = ox + 2a*cosd(ea)
       y1 = oy + 2a*sind(ea)
       segment(ox, oy, x1, y1, :red)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x, y, "(x,y)")
       point(a, -√3a/3, "(a,-√3a/3) ", :magenta, :right, :bottom, delta=delta/2)
       point(0, 2√3a/3, " 2√3a/3", :magenta, :left, :vcenter)
       point(0, R, " R", :blue, :center, :bottom, delta=delta/2)
       point(√3a, 2√3a/3 + a)
   end
end;

算額（その1100）

算額（その1100）

六十六 岩手県花泉町金沢字大柳 金沢八幡宮 明治29年(1896)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，二等辺三角形4個，半円1個

半円の中に二等辺三角形を 4 個，大円 1 個，小円 2 個を容れる。小円の直径が与えられたとき，大円の直径を求めよ。

半円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
小円の半径と中心座標を r2, (R/2, y2)
二等辺三角形の高さを y0
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms R::positive, r1::positive,
     r2::positive, y2::positive, y0::positive
y0 = √Sym(7)R/4  # y0 = sqrt(R^2 - (3R/4)^2)
eq1 = R^2/4 + y2^2 - (R - r2)^2 |> expand
eq2 = r2/y0 - r1 /(R - r1)
eq2 = r2/y2 - r1 /(R - r1)
eq3 = dist2(0, 0, R/4, y0, R/2, y2, r2)
eq4 = dist2(0, 0, R/4, y0, 0, R - r1, r1)
res = solve([eq1, eq2, eq4], (R, r1, y2))[1]

   (2*r2*(5*sqrt(9 - 4*sqrt(2)) + 14 + 10*sqrt(18 - 8*sqrt(2)))/21, 2*r2*(-2 + 4*sqrt(2) + 5*sqrt(9 - 4*sqrt(2)))/21, 2*sqrt(2)*r2)

それぞれの解は簡約化できるものもある。

#= R =# res[1] |> sympy.sqrtdenest |> simplify |> println

   14*r2/3

#= r1 =# res[2] |> sympy.sqrtdenest |> simplify |> println

   2*r2*(-1 + 2*sqrt(2))/3

#= y2 =# res[3] |> println

   2*sqrt(2)*r2

大円の半径 r1 は，小円の半径 r2 の (4√2 - 2)/3 倍である。
小円の直径が 1 寸のとき，大円の直径は 1.2189514164974602 寸である。

その他のパラメータは以下のとおりである。

   r2 = 0.5;  R = 2.33333;  r1 = 0.609476;  y2 = 1.41421;  y0 = 1.54335

「術」では，小円の直径の (70 - √1372)/27 = 1.220721542410953 としているので，食い違いがある。

原因は図形の解釈にあるかもしれない。
いつもの通り，山村の図が不正確であり（算額の図も同じかもしれないが），左右の二等辺三角形の頂点が半円の円周上にあるかどうか不明瞭である。
山村の図では右の二等辺三角形の頂点は円周上にないが，左のそれは円周上にあるように見える。
ここでは，頂点は円周上にあるものとして解いた（そのほうが算額らしいと思うので）。しかし，別途，円周上にないとして解いた場合でも 1.2260924510696558 となり，やはり「術」の解とは一致しなかった。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (R, r1, y2) = r2 .* (14/3, (4√2 - 2)/3, 2√2)
   y0 = √7R/4
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r2, 2r1)
   @printf("r2 = %g;  R = %g;  r1 = %g;  y2 = %g;  y0 = %g\n", r2, R, r1, y2, y0)
   plot(R .* [1, 3/4, 1/2, 1/4, 0, -1/4, -1/2, -3/4, -1, 1], [0, y0, 0, y0, 0, y0, 0, y0, 0, 0], color=:magenta, lw=0.5)
   circle(0, 0, R, :blue, beginangle=0, endangle=180)
   circle(0, R - r1, r1)
   circle2(R/2, y2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R/4, 0, "R/4", :magenta, :center, delta=-delta)
       point(R/2, 0, "R/2", :magenta, :center, delta=-delta)
       point(3R/4, 0, "3R/4", :magenta, :center, delta=-delta)
       point(3R/4, y0, " (3R/4,y0)", :magenta, :left, :vcenter)
       point(R/2, y2, "小円:r2\n(R/2,y2)", :green, :center, delta=-delta)
       point(0, R - r1, "大円:r1\n(0,R-r1)", :red, :center, delta=-delta)
       point(0, R, "R", :blue, :center, :bottom, delta=delta)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta)
       plot!(ylims=(-8delta, R + 2delta))
   end
end;

算額（その1099）

算額（その1099）

六十六 岩手県花泉町金沢字大柳 金沢八幡宮 明治29年(1896)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，外円，直角三角形2個

全円の中に交差する（合同な）直角三角形を 2 個と，大円，小円を 1 個ずつ容れる。大円と小円の直径が与えられたとき，全円の直径を求めよ。

内接する直角三角形なので，斜辺は全円の直径である。一つの直角三角形の斜辺が x 軸上になるように図を描く。
全円の半径と中心座標を　R, (0, 0)
大円の直径と中心座標を r1, (x1, r1); x1 < 0
小円の半径と中心座標を r2, (0, R - r2)
直角三角形の直径上ではない直角の頂点の座標を (x0, y0)
とおき，以下の方程式を解く。

なお，証明はしないが x1 = r2 - r1 である（図の水色の垂直線を参照）ので，方程式の解は簡単に求まる。

include("julia-source.txt")

using SymPy
@syms R::positive, x0::positive, y0::positive,
     r1::positive, x1::negative, r2::positive
y0 = sqrt(R^2 - x0^2)
x1 = r2 - r1  # 未証明
eq1 = x1^2 + r1^2 - (R - r1)^2
eq2 = dist2(-x0, y0, x0, -y0, -x1, r1, r1)
eq3 = dist2(-R, 0, x0, y0, 0, R - r2, r2);

最初に eq1 を解くことで全円の半径 R が求まる。「術」と同じ式になる。

ans_R = solve(eq1, R)[2]
ans_R |> println

   r1 + sqrt(2*r1^2 - 2*r1*r2 + r2^2)

次いで，eq2 を解いて x0 を求める。
なお，eq3 を解いても求まるが，本質的におなじ式であるが eq3 から求める式は SymPy では簡約化できず，長く複雑なものになる。

ans_x0 = solve(eq2, x0)[3] |> factor
ans_x0 |> println

   R*r2*(2*r1 - r2)/(2*r1^2 - 2*r1*r2 + r2^2)

大円，小円の直径が 20, 10 のとき，全円の直径は 42.3607 である。

   r1 = 10;  r2 = 5;  R = 21.1803;  x0 = 12.7082;  y0 = 16.9443;  x1 = -5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (10, 5)
   R = r1 + sqrt(2*r1^2 - 2*r1*r2 + r2^2)
   x0 = R*r2*(2*r1 - r2)/(2*r1^2 - 2*r1*r2 + r2^2)
   y0 = sqrt(R^2 - x0^2)
   x1 = r2 - r1  # 未証明
   @printf("大円，小円の直径が %g, %g のとき，全円の直径は %g である。\n", 2r1, 2r2, 2R)
   @printf("r1 = %g;  r2 = %g;  R = %g;  x0 = %g;  y0 = %g;  x1 = %g\n", r1, r2, R, x0, y0, x1)
   plot()
   circle(0, 0, R, :blue)
   circle(x1, -r1, r1)
   circle(0, R - r2, r2, :green)
   plot!([x0, -x0, R, x0], [-y0, y0, 0, -y0], color=:magenta, lw=0.5)
   plot!([R, -R, x0, R], [0, 0, y0, 0], color=:magenta, lw=0.5)
   vline!([r2], lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, -r1, "大円:r1,(x1,-r1)", :red, :center, delta=-delta/2)
       point(0, R - r2, "小円:r2,(0,R-r2)", :green, :center, delta=-delta/2)
       point(r2, 0, "r2", :green, :center, delta=-delta/2)
       point(x0, y0, "(x0,y0)  ", :magenta, :right, :bottom, delta=-delta/2)
       point(x0, -y0, "(x0,-y0)  ", :magenta, :right, :bottom, delta=-delta/2)
       point(-x0, y0, "  (-x0,y0)", :magenta, :left, :bottom, delta=-delta/2)
   end
end;