算額（その1040）

算額（その1040）

八十三 藤沢町保呂羽保呂羽山 保呂羽神社 明治26年(1893)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

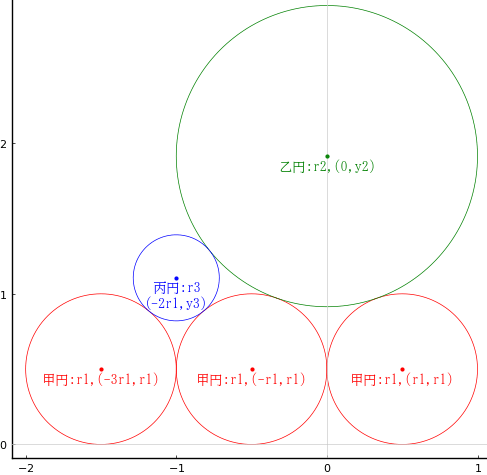
直線の上に甲円，乙円が互いに接して載っている。その 2 つの円の上に丙円が載っている。3 個の円の直径が与えられたとき，丙円のてっぺんまでの高さを求めよ。

甲円の半径と中心座標を r1, (x1, r1)
乙円の半径と中心座標を r2, (0, r2)
丙円の半径と中心座標を r3, (x3, y3)
とおき，以下の連立方程式を解く。
高さは y3 + r3 である。

include("julia-source.txt");

using SymPy
@syms r1::positive, x1::positive, r2::positive,
     r3::positive, x3::positive, y3
eq1 = x1^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand
eq2 = (x1 - x3)^2 + (y3 - r1)^2 - (r1 + r3)^2 |> expand
eq3 = x3^2 + (y3 - r2)^2 - (r2 + r3)^2 |> expand
#res = solve([eq1, eq2, eq3], (x1, x3, y3))[1];  # 1 of 2

SymPy で解くと，x1 の式が信じられないくらい長くなってしまうので，別途解く。
x1 = 2sqrt(r1*r2) である。ちなみに，「算法助術」の公式40ではある。

ans_x1 = solve(eq1, x1)[1]
ans_x1 |> println

   2*sqrt(r1)*sqrt(r2)

x3, y3 も別々に解いたほうが若干短くなるが，連立方程式として解く。eq2 は x1 を含むので，代入しておく。

eq2 = eq2(x1 => ans_x1);
(ans_x3, ans_y3) = solve([eq2, eq3], (x3, y3))[2];  # 2 of 2

ans_x3 = ans_x3 |> factor
ans_x3 |> println

   2*sqrt(r1)*sqrt(r2)*(r1*r2 - r1*sqrt(r3)*sqrt(r1 + r2 + r3) - r1*r3 + r2^2 + r2*sqrt(r3)*sqrt(r1 + r2 + r3) + r2*r3)/(r1 + r2)^2

ans_y3 = ans_y3 |> factor
ans_y3 |> println

   (2*r1^2*r2 - r1^2*r3 + 2*r1*r2^2 + 4*r1*r2*sqrt(r3)*sqrt(r1 + r2 + r3) + 2*r1*r2*r3 - r2^2*r3)/(r1 + r2)^2

ans_x1(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println
ans_x3(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println
ans_y3(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println

   3.87298334620742
   0.669041418324543
   3.90881372890605

高さは,ans_y3 + r3 = 3.90881372890605 + 1 = 4.9088137289060505 である。

高さだけを求めるならば，「算法助術」の公式47を適用する。

@syms h
公式47 = r1*h + r2*h - 2r1*r2 - 2sqrt(2r1*r2*r3*h)
res = solve(公式47, h)[2]
res |> println

   2*r1*r2*(r1 + r2 + 2*sqrt(r3)*sqrt(r1 + r2 + r3) + 2*r3)/(r1^2 + 2*r1*r2 + r2^2)

res(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println

   4.90881372890605

「術」も，簡約化した結果の見た目は異なるが，公式47と等価である。

@syms r1, r2, r3
天 = 2(r1 + r2 + r3)
A = sqrt(天 * 2r3)*2
B = 天 - A + 2r3
高 = 2r1*2r2/B |> simplify
高 |> println

   2*r1*r2/(r1 + r2 + 2*r3 - 2*sqrt(r3*(r1 + r2 + r3)))

高(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println

   4.90881372890605

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3) = (5, 3, 2) ./ 2
   x1 = 2*sqrt(r1)*sqrt(r2)
   x3 = 2*sqrt(r1)*sqrt(r2)*(r1*r2 - r1*sqrt(r3)*sqrt(r1 + r2 + r3) - r1*r3 + r2^2 + r2*sqrt(r3)*sqrt(r1 + r2 + r3) + r2*r3)/(r1 + r2)^2
   y3 = (2*r1^2*r2 - r1^2*r3 + 2*r1*r2^2 + 4*r1*r2*sqrt(r3)*sqrt(r1 + r2 + r3) + 2*r1*r2*r3 - r2^2*r3)/(r1 + r2)^2
   @printf("甲円，乙円，丙円の直径がそれぞれ %g, %g, %g のとき，盤面から丙円のてっぺんまでの高さは %g である。\n", 2r1, 2r2, 2r3, y3 + r3)
   @printf("x1 = %g;  x3 = %g;  y3 = %g\n",x1, x3, y3)
   plot()
   circle(x1, r1, r1)
   circle(0, r2, r2, :green)
   circle(x3, y3, r3, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, r1, "甲円:r1,(x1,r1)", :red, :center, delta=delta)
       point(0, r2, "乙円:r2,(0,r2)", :green, :center, delta=delta)
       point(x3, y3, "丙円:r3,(x3,y3)", :blue, :center, delta=delta)
       point(x3, y3 + r3, "高さ=y3+r3", :magenta, :center, :bottom, delta=delta)
   end
end;

算額（その1039）

算額（その1039）

八十二 藤沢町保呂羽保呂羽山 保呂羽神社 明治7年(1874)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

大円の中に中円 2 個，小円 5 個を容れる。小円の直径が 1 寸のとき，中円の直径はいかほどか。

大円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を 2r3, (x32, 0); x32 = x3 - 3r3 < 0
小円の半径と中心座標を r3, (x3, r3), x(3 - 3r3, 0)
とおき以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r3::positive, x3::positive
x32 = x3 - 3r3
eq1 = x32^2 + r3^2 - (R - 2r3)^2
eq2 = x3^2 + r3^2 - (R - r3)^2;
res = solve([eq1, eq2], (R, x3))[2]  # 2 of 2

   (-3*r3 + 3*r3*(sqrt(6)/4 + 3/2), r3*(sqrt(6)/4 + 3/2))

res[1] |> simplify |>  println

   3*r3*(2 + sqrt(6))/4

大円の半径は小円の半径の 3(2 + √6)/4 倍である。
小円の直径が 1 寸のとき，大円の直径は 3.337117307087383 寸である。

その他のパラメータは以下のとおりである。
r3 = 0.5;  R = 1.66856;  x3 = 1.05619;  x32 = -0.443814

3(2 + √6)/4

   3.337117307087383

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   (R, x3) = (-3*r3 + 3*r3*(sqrt(6)/4 + 3/2), r3*(sqrt(6)/4 + 3/2))
   x32 = x3 - 3r3
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r3, 2R)
   @printf("r3 = %g;  R = %g;  x3 = %g;  x32 = %g\n", r3, R, x3, x32)
   plot()
   circle(0, 0, R)
   circle22(x32, 2r3, r3, :green)
   circle22(x32, r3, 2r3, :blue)
   circle22(x3, r3, r3, :green)
   circle(x32, 0, r3, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x3, r3, "小円:r3,(x3,r3)", :green, :center, delta=-delta/2)
       point(x32, 0, "小円:r3,(x32,0)", :green, :center, delta=-delta/2)
       point(x32, r3, "中円:r2\n(x32,r3)", :blue, :center, :bottom, delta=delta)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その47）

算額（その47）

岩手県東磐井郡藤沢町 藤勢寺 元治 2 年
http://www.wasan.jp/iwate/fujise.html

七十九 藤沢町藤沢道場 藤勢寺 元治2年
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

前者のリンクは，画像が不鮮明で，問，答，術とも正確に読めていなかった。
後者のリンク内容に基づき，第二版を作成する。

1 辺が 1 寸の正方形に2種類の円が収まっている。それぞれの径を求めよ。
注：算額の図では円が2種類あるように見えるが，問では「小円6個」と書いてある。

正方形の一辺の長さを a
小円の半径と中心座標を r, (x1, r), (r, x1), (x2, x2)
菱形の頂点座標を (x0, x0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a::positive, r::positive,
     x0::positive, x1::positive, x2::positive;
eq1 = dist2(a, 0, 0, a, x2, x2, r)
eq2 = dist2(a, 0, x0, x0, x2, x2, r)
eq3 = dist2(a, 0, x0, x0, x1, r, r)
eq4 = dist2(0, 0, a, a, x1, r, r)
res = solve([eq1, eq2, eq3, eq4], (r, x0, x1, x2))[6]  # 6 of 8

   (a*(-4553*sqrt(-10 + 12*sqrt(2)) - 4605*sqrt(-5 + 6*sqrt(2)) - 3537 + 17080*sqrt(2))/(2*(-4663*sqrt(-5 + 6*sqrt(2)) - 351*sqrt(2)*sqrt(-5 + 6*sqrt(2)) + 3845 + 4092*sqrt(2))), a*(-104*sqrt(2) - 3 + 25*sqrt(-10 + 12*sqrt(2)) + 45*sqrt(-5 + 6*sqrt(2)))/(12*(-6*sqrt(2) + 1 + 4*sqrt(-5 + 6*sqrt(2)))), (-4*sqrt(2)*a*sqrt(-5 + 6*sqrt(2)) - 5*a*sqrt(-5 + 6*sqrt(2)) + 5*sqrt(2)*a + 13*a)/(8 - 4*sqrt(-5 + 6*sqrt(2))), a*(-sqrt(2)/8 + 1/4 + sqrt(-5/32 + 3*sqrt(2)/16)))

a = 10
r = a*(-4553*sqrt(-10 + 12√2) - 4605*sqrt(-5 + 6√2) - 3537 + 17080√2)/(2*(-4663*sqrt(-5 + 6√2) - 351√2*sqrt(-5 + 6√2) + 3845 + 4092√2))
x0 = a*(-104√2 - 3 + 25*sqrt(-10 + 12√2) + 45*sqrt(-5 + 6√2))/(12*(-6√2 + 1 + 4*sqrt(-5 + 6√2)))
x1 = (-4√2a*sqrt(-5 + 6√2) - 5*a*sqrt(-5 + 6√2) + 5√2a + 13*a)/(8 - 4*sqrt(-5 + 6√2))
x2 = a*(-sqrt(2)/8 + 1/4 + sqrt(-5/32 + 3√2/16))
(r, x0, x1, x2)

   正方形の一辺の長さが 10 のとき，小円の直径は 2.73661 である。
   a = 10;  r = 1.36831;  x0 = 2.98964;  x1 = 3.30338;  x2 = 4.03246

r は，a の 6次式を解いて求めることができる。
山村は「術の式（の係数）に誤りがある」として，訂正の上で解を求めたが，「許容範囲内の誤差がある」と言っているが，そもそも山村が訂正した係数にも誤りがあるし，さらに言えば，係数は整数ではない。
どのような 6 次式なのか，手作業で方程式を解いてみる。
方針としては，eq1, eq2, eq4 の連立方程式から(a, r を含む） x0, x1, x2 （の式）を求めて，eq3 に代入して a, r を含む 式を求め，r について解く。 

res = solve([eq1, eq2, eq4], (x0, x1, x2))[3]  # 3 of 4

   ((a^3 - 4*a^2*(a/2 - sqrt(2)*r/2) + 2*a*r^2)/(-2*a^2 + 4*r^2), r*(1 + sqrt(2)), a/2 - sqrt(2)*r/2)

eq = eq3(x0 => res[1], x1 => res[2]) |> expand |> simplify
eq = numerator(eq)/a^2

    a^6/100 - 3*sqrt(2)*a^5*r/50 - a^5*r/25 + 3*sqrt(2)*a^4*r^2/25 + 6*a^4*r^2/25 - 2*sqrt(2)*a^3*r^3/25 - 8*sqrt(2)*a^2*r^4/25 - 11*a^2*r^4/25 + 2*sqrt(2)*a*r^5/25 + 4*a*r^5/25 + 4*r^6/25 + 4*sqrt(2)*r^6/25

a に定数を代入して eq = 0 を解けば r が求まる。
a = 10 としたとき，
38.62741699796952r^6+ 273.1370849898476r^5 -8925.483399593904r^4 -11313.70849898476r^3 +409705.6274847714r^2 -1.248528137423857e6r+ 1000000 = 0
である。係数は整数ではないので，「術」や山村のように整数係数を使用しても，正しい解は得られない。グラフを描けば，近似解すら得られないことがわかる。
SymPy でも解を得られないので，ニュートン・ラフソン法で数値解を求める。

function newton(fun, x1; delta = 1e-5, epsilon = 1e-14, maxrotation = 100)
   fun2(x) = (fun(x + delta) - fun(x)) / delta
   for i = 1:maxrotation
       x2 = x1 - fun(x1) / fun2(x1)
       if abs((x2 - x1) / x2) < epsilon
           return x2
       end
       x1 = x2
   end
   error("収束しませんでした")
end;

関数定義
fun(r) = 16*r^6 + 16*sqrt(2)*r^6 + 80*sqrt(2)*r^5 + 160*r^5 - 3200*sqrt(2)*r^4 - 4400*r^4 - 8000*sqrt(2)*r^3 + 120000*sqrt(2)*r^2 + 240000*r^2 - 600000*sqrt(2)*r - 400000*r + 1000000;

r = newton(fun , 1.368)
a = 10
x0 = a*(a^2 - 2*sqrt(2)*a*r - 2*r^2)/(2*(a^2 - 2*r^2))
x1 = r*(1 + sqrt(2))
x2 = a/2 - sqrt(2)*r/2
(r, x0, x1, x2)

   (1.368306828856772, 2.989643583187269, 3.30338490371374, 4.032460962571516)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 10
   r = a*(-4553*sqrt(-10 + 12√2) - 4605*sqrt(-5 + 6√2) - 3537 + 17080√2)/(2*(-4663*sqrt(-5 + 6√2) - 351√2*sqrt(-5 + 6√2) + 3845 + 4092√2))
   x0 = a*(-104√2 - 3 + 25*sqrt(-10 + 12√2) + 45*sqrt(-5 + 6√2))/(12*(-6√2 + 1 + 4*sqrt(-5 + 6√2)))
   x1 = (-4√2a*sqrt(-5 + 6√2) - 5*a*sqrt(-5 + 6√2) + 5√2a + 13*a)/(8 - 4*sqrt(-5 + 6√2))
   x2 = a*(-sqrt(2)/8 + 1/4 + sqrt(-5/32 + 3√2/16))
   @printf("正方形の一辺の長さが %g のとき，小円の直径は %g である。\n", a, 2r)
   @printf("a = %g;  r = %g;  x0 = %g;  x1 = %g;  x2 = %g\n", a, r, x0, x1, x2)
   #plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
   plot([0, x0, a, a - x0, 0, a, a, 0, 0, a], [a, x0, 0, a - x0, a, 0, a, a, 0, 0], color=:blue, lw=0.5)
   segment(0, 0, x0, x0, :blue)
   segment(a, a, a - x0, a - x0, :blue)
   circle(x1, r, r)
   circle(r, x1, r)
   circle(x2, x2, r)
   circle(a - x1, a - r, r)
   circle(a - r, a - x1, r)
   circle(a - x2, a - x2, r)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(x0, x0, "(x0,x0)", :black, :left, :bottom, delta=delta/2)
       point(x1, r, "小円:r,(x1,r)", :red, :center, delta=-delta/2)
       point(x2, x2, "小円:r,(x2,x2)", :red, :center, delta=-delta/2)
   end
end;

算額（その1038）

算額（その1038）

七十九 藤沢町藤沢道場 藤勢寺 元治2年
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

外円の中に交差する正方形を2個入れ，区分された領域に小円を 3 個容れる。外円の直径が 10 寸のとき，正方形の一辺の長さはいかほどか。

外円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, 0), (R - r, 0)
正方形の一辺の長さを a
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, a::positive
b = a/√Sym(2)
eq1 = dist2(0, R - 2b, b, R - b, R - r, 0, r)
eq2 = dist2(0, R - 2b, b, R - b, 0, 0, r)
res = solve([eq1, eq2], (a, r))[2]  # 2 of 3

   (-R/7 + 11*sqrt(2)*R/14, R*(-1/7 + 2*sqrt(2)/7))

正方形の一辺の長さは a = -R/7 + 11*sqrt(2)*R/14 = R(11√2 - 2)/14 である。
外円の半径が 5 寸（直径が 10）寸のとき，5(11√2 - 2)/14 = 4.841553280751445 寸である。

「答」は 4.114 寸であるが，それでは小さすぎる。図を描いてみればわかる。山村も算額の「術」をそのまま書き写しているので，答えが変である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 10/2
   (a, r) = (-R/7 + 11*sqrt(2)*R/14, R*(-1/7 + 2*sqrt(2)/7))
   b = a/√2
   plot([0, b, 0, -b, 0], [R - 2b, R - b, R, R - b, R - 2b], color=:blue, lw=0.5)
   plot!([0, b, 0, -b, 0], -[R - 2b, R - b, R, R - b, R - 2b], color=:blue, lw=0.5)
   circle(0, 0, R, :green)
   circle2(R - r, 0, r)
   circle(0, 0, r)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(b, R - b, "(a/√2,R-a/√2) ", :blue, :right, :vcenter)
       point(0, R - 2b, " (0,R-2a/√2)", :blue, :left, :vcenter)
       point(R - r, 0, "小円:r,(R-r,0)", :red, :center, delta=-delta/2)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
   end
end;

算額（その1037）

算額（その1037）

七十八 藤沢町藤沢早道 竹駒神社 元治2年(1865)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

直線の上に甲円，乙円，丙円が載っている。甲円，乙円の直径がそれぞれ 1 寸，2 寸のとき，丙円の直径はいかほどか。

甲円の半径と中心座標を r1, (r1, r1), (-r1, r1), (-3r1, r1)
乙円の半径と中心座標を r2, (0, y2)
丙円の半径と中心座標を r3, (-r1, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, y2::positive,
     r3::positive, y3::positive
eq1 = r1^2 + (y2 - r1)^2 - (r1 + r2)^2
eq2 = 4r1^2 + (y2 - y3)^2 - (r2 + r3)^2
eq3 = r1^2 + (y3 - r1)^2 - (r1 + r3)^2
res = solve([eq1, eq2, eq3], (r3, y3, y2))[4] ## 4 of 4

   ((-2*r1^3 + 5*r1^2*r2 - r1*r2^2 - 2*r2^3 + 2*r2*sqrt(4*r1^4 - 4*r1^3*r2 - 3*r1^2*r2^2 + 2*r1*r2^3 + r2^4))/(r1^2 - 5*r1*r2 + 4*r2^2), (r1^2 - r1*sqrt(r2)*sqrt(2*r1 + r2) - 4*r1*r2 - 2*r2^(3/2)*sqrt(2*r1 + r2) + 2*sqrt(r2)*sqrt(2*r1^3 - 3*r1^2*r2 + r2^3))/(r1 - 4*r2), r1 + sqrt(r2)*sqrt(2*r1 + r2))

1.　手動による簡約化

丙円の半径 r3 は SymPy では簡約化できていないので，手作業で簡約化する。
方針としては，分子と分母を別々に簡約化（因数分解）して，結果を割り算する。

r3 = res[1]

まず，分子について検討する。平方根内の数式を因数分解する。

4*r1^4 - 4*r1^3*r2 - 3*r1^2*r2^2 + 2*r1*r2^3 + r2^4 |> factor |>println

   (r1 - r2)^2*(2*r1 + r2)^2

平方根内は二乗項の積であるが， r1 < r2 のため，ルートを外したときの符号が変わることに注意する。
因数分解をして，結果として -r1*(r1 - r2)*(2*r1 + r2) になる。

num = (-2*r1^3 + 5*r1^2*r2 - r1*r2^2 - 2*r2^3 - 2*r2*(r1 - r2)*(2*r1 + r2)) |> factor

  -r1*(r1 - r2)*(2*r1 + r2)

次に，分母を因数分解する。
結果として，(r1 - 4*r2)*(r1 - r2) になる。

den = denominator(r3)|> factor

  (r1 - 4*r2)*(r1 - r2)

「分子/分母」を計算すると，約分できるb場合には自動的に約分される。
結果として -r1*(2*r1 + r2)/(r1 - 4*r2) を得る。
これは，当然であるが，術で述べられたものと同じである。

(num/den) |> println

   -r1*(2*r1 + r2)/(r1 - 4*r2)

甲円，乙円の直径がそれぞれ 1，2 のとき，丙円の直径は 0.571429 である。

その他のパラメータは以下のとおりである。
   r1 = 0.5;  r2 = 1;  y2 = 1.91421;  r3 = 0.285714;  y3 = 1.10609

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (1, 2) ./ 2
   (r3, y3, y2) = ((-2*r1^3 + 5*r1^2*r2 - r1*r2^2 - 2*r2^3 + 2*r2*sqrt(4*r1^4 - 4*r1^3*r2 - 3*r1^2*r2^2 + 2*r1*r2^3 + r2^4))/(r1^2 - 5*r1*r2 + 4*r2^2), (r1^2 - r1*sqrt(r2)*sqrt(2*r1 + r2) - 4*r1*r2 - 2*r2^(3/2)*sqrt(2*r1 + r2) + 2*sqrt(r2)*sqrt(2*r1^3 - 3*r1^2*r2 + r2^3))/(r1 - 4*r2), r1 + sqrt(r2)*sqrt(2*r1 + r2))
   @printf("甲円，乙円の直径がそれぞれ %g，%g のとき，丙円の直径は %g である。\n", 2r1, 2r2, 2r3)
   @printf("その他のパラメータは以下のとおりである。\nr1 = %g;  r2 = %g;  y2 = %g;  r3 = %g;  y3 = %g\n", r1, r2, y2, r3, y3)
   plot()
   circle2(r1, r1, r1)
   circle(-3r1, r1, r1)
   circle(0, y2, r2, :green)
   circle(-2r1, y3, r3, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(-3r1, r1, "甲円:r1,(-3r1,r1)", :red, :center, delta=-delta/2)
       point(-r1, r1, "甲円:r1,(-r1,r1)", :red, :center, delta=-delta/2)
       point(r1, r1, "甲円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(0, y2, "乙円:r2,(0,y2)", :green, :center, delta=-delta/2)
       point(-2r1, y3, "丙円:r3\n(-2r1,y3)", :blue, :center, delta=-delta/2)
   end
end;