算額（その1149）

算額（その1149）

番外九 武州 慈恩寺 
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円2個，正三角形

正方形と大円が直線上に載っている正方形の大円寄りにある頂点を通る大円の接線と，正方形の上辺を延長した直線と正方形の辺の 3 点で接する小円を描く。大円の直径が 12 寸，正方形の一辺の長さが 10 寸のとき，小円の直径はいかほどか。

正方形の一辺の長さを a
大円の半径と中心座標を r1, (r1, r1)
小円の半径と中心座標を r2, (-a - r2, a - r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive
eq1 = dist2(-a, b, 0, a, r1, r1, r1)
eq2 = dist2(-a, b, 0, a, -a -r2, a - r2, r2)
res = solve([eq1, eq2], (r2, b))[1]

   ((a^2 - 2*a*r1)/(-2*a + 2*r1), a*(-a^2 + 2*r1^2)/(2*r1*(-a + r1)))

小円の半径は (a^2 - 2*a*r1)/(-2*a + 2*r1) である。

正方形の一辺の長さが 10，大円の直径が 12 のとき，小円の直径は 5 である。

function draw(a, r1, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, b) = ((a^2 - 2*a*r1)/(-2*a + 2*r1), a*(-a^2 + 2*r1^2)/(2*r1*(-a + r1)))
   @printf("正方形の一辺の長さが %g，大円の直径が %g のとき，小円の直径は %g である。\n", a, 2r1, 2r2)
   plot([-a, 0, 0, -a, -a], [0, 0, a, a, 0], color=:blue, lw=0.5)
   circle(r1, r1, r1)
   circle(-a - r2, a - r2, r2, :green)
   abline(-a, b, (a - b)/a, -a - 2r2, 1.3r1)
   segment(-a - 2r2, a, -a, a, :black)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r1, "大円:r1,(r1,r1)", :red, :center, delta=-delta)
       point(-a - r2, a - r2, "小円:r2,(-a-r2,a-r2)", :black, :left, :bottom, delta=delta, deltax=-12delta)
       point(0, a, "a", :blue, :center, :bottom, delta=delta)
       point(-a, a, "(-a,a)", :blue, :center, :bottom, delta=delta)
       point(-a, b, " (-a,b)", :black, :left, delta=-delta/2)
   end
end;

算額（その1148）

算額（その1148）

番外三 川口市峯後 峯が岡八幡宮 （昭和10年代よりは前）
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円2個，直角三角形，正三角形

直角三角形内に大円，小円，正三角形を容れる。鈎（直角を挟む二辺の短い方）が 5 寸のとき，図形の各寸法を得よ。

大円の半径と中心座標を r1, (r1, y1)
小円の半径と中心座標を r2, (r2, r2)
正三角形の頂点の座標を (a, 0), (b, 0), ((a + b)/2, √3(b - a)/2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms 鈎::positive, a::positive, b::positive,
     r1::positive, y1::positive, r2::positive
s3 = √Sym(3)
eq1 = dist2(a, 0, (a + b)/2, s3*(b - a)/2, r1, y1, r1)
eq2 = dist2(a, 0, (a + b)/2, s3*(b - a)/2, r2, r2, r2)
eq3 = dist2(0, 鈎, 2b - a, 0, r1, y1, r1)
eq4 = (r1 - r2)^2 + (y1 - r2)^2 - (r1 + r2)^2
eq5 =  s3*鈎 - (2b - a);

まず，eq1, eq2, eq4, eq5 を解いて a, b, y1, y2 を求める。

(ans_a, ans_b, ans_y1, ans_r2) = solve([eq1, eq2, eq4, eq5], (a, b, y1, r2))[1]

   (r1*(-9*sqrt(3) - 12*sqrt(26 - 15*sqrt(3)) - 4*sqrt(78 - 45*sqrt(3)) + 21)/3, -3*sqrt(3)*r1/2 - 2*r1*sqrt(26 - 15*sqrt(3)) - 2*r1*sqrt(78 - 45*sqrt(3))/3 + 7*r1/2 + sqrt(3)*鈎/2, r1*(-6*sqrt(3) + 4*sqrt(26 - 15*sqrt(3)) + 4*sqrt(78 - 45*sqrt(3)) + 11), r1*(-8*sqrt(3) - 4*sqrt(26 - 15*sqrt(3)) + 15))

ans_a = ans_a |> sympy.sqrtdenest |> factor
ans_a |> println

   r1*(-8*sqrt(6) - 9*sqrt(3) + 12*sqrt(2) + 21)/3

ans_b = ans_b |> sympy.sqrtdenest |> factor
ans_b |> println

   (-8*sqrt(6)*r1 - 9*sqrt(3)*r1 + 12*sqrt(2)*r1 + 21*r1 + 3*sqrt(3)*鈎)/6

ans_y1 = ans_y1 |> sympy.sqrtdenest |> factor
ans_y1 |> println

   r1*(-6*sqrt(3) - 4*sqrt(6) + 11 + 8*sqrt(2))

ans_r2 = ans_r2 |> sympy.sqrtdenest |> simplify
ans_r2 |> println

   r1*(-6*sqrt(6) - 8*sqrt(3) + 10*sqrt(2) + 15)

これらを eq13 に代入する。

eq13 = eq3(a => ans_a, b => ans_b, y1 => ans_y1, r2 => ans_r2) |> simplify
eq13 |> println

   鈎^2*(-536*sqrt(6)*r1^2 - 758*sqrt(3)*r1^2 + 1320*r1^2 + 936*sqrt(2)*r1^2 - 48*sqrt(2)*r1*鈎 - 66*r1*鈎 + 24*sqrt(6)*r1*鈎 + 34*sqrt(3)*r1*鈎 + 3*鈎^2)

eq13 を解いて r1 を求める。

ans_r1 = solve(eq13, r1)[1];
ans_r1 |> println

   鈎*(-19*sqrt(3) - 12*sqrt(6) + 33 + 24*sqrt(2))/(2*(-268*sqrt(6) - 379*sqrt(3) + 660 + 468*sqrt(2)))

den = denominator(ans_r1) |> sympy.sqrtdenest |> simplify
ans_r1 = numerator(ans_r1)/den
ans_r1 = apart(ans_r1) |> simplify
ans_r1 |> println

   鈎*(-16*sqrt(6) - 4*sqrt(2) + 19 + 29*sqrt(3))/94

鈎 = 5 を代入すると数値解が得られる。

ans_r1(鈎 => 5).evalf() |> println

   1.29685017475927

全てのパラメータは以下のように計算される。

鈎 = 5
r1 = 鈎*(-16*sqrt(6) - 4*sqrt(2) + 19 + 29*sqrt(3))/94
r2 = r1*(-6*sqrt(6) - 8*sqrt(3) + 10*sqrt(2) + 15)
y1 = r1*(-6*sqrt(3) - 4*sqrt(6) + 11 + 8*sqrt(2))
b = (-8*sqrt(6)*r1 - 9*sqrt(3)*r1 + 12*sqrt(2)*r1 + 21*r1 + 3*sqrt(3)*鈎)/6
a = r1*(-8*sqrt(6) - 9*sqrt(3) + 12*sqrt(2) + 21)/3
println("正三角形の一辺の長さ = $(b - a)")
println("大円の直径 = $(2r1)")
println("小円の直径 = $(2r2)")

   正三角形の一辺の長さ = 3.727915719641115
   大円の直径 = 2.593700349518533
   小円の直径 = 1.5271466611926818

「答」では以下のようになっている。
正三角形の一辺の長さ = 3.66
大円の直径 = 2.68
小円の直径 = 1.55
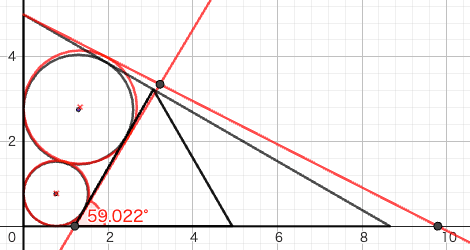
小数点以下2位までしか書かれていないので比較しても意味がないが，少なくとも，このパラメータで図を描くと赤のようになり，上で求めた正確な図（黒）とは違う。大円と小円の共通接線が水辺線となす角は 60° にならない。



2位までしか書かれていないから不正確なのではなく，「術」に疑問がある。たとえば正三角形の一辺の長さは

鈎 = 5
甲 = sqrt(3) + 1
三角面 = (鈎 / 甲)*2

で求めるとしているが，これで計算すると三角面は 3.6602540378443864 となり，そもそも正しい値 3.727915719641115 とは異なった術式である。

function draw(鈎, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 鈎*(-16*sqrt(6) - 4*sqrt(2) + 19 + 29*sqrt(3))/94
   r2 = r1*(-6*sqrt(6) - 8*sqrt(3) + 10*sqrt(2) + 15)
   y1 = r1*(-6*sqrt(3) - 4*sqrt(6) + 11 + 8*sqrt(2))
   b = (-8*sqrt(6)*r1 - 9*sqrt(3)*r1 + 12*sqrt(2)*r1 + 21*r1 + 3*sqrt(3)*鈎)/6
   a = r1*(-8*sqrt(6) - 9*sqrt(3) + 12*sqrt(2) + 21)/3
   @printf("大正三角形の一辺の長さが %g のとき，正方形の一辺の長さは %g である。\n", 2a, 2b)
   plot([0, 2b - a, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   plot!([a, b, (a + b)/2, a], [0, 0, √3(b - a)/2, 0], color=:magenta, lw=0.5)
   circle(r1, y1, r1)
   circle(r2, r2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :magenta, :left, :bottom, delta=delta/2)
       point(b, 0, " b", :magenta, :left, :bottom, delta=delta/2)
       point(2b - a, 0, " 2b-a", :blue, :left, :bottom, delta=delta/2)
       point(0, 鈎, " 鈎", :blue, :left, :bottom, delta=delta/2)
       point((a + b)/2, √3*(b - a)/2, "((a+b)/2,√3(b-a)/2)", :magenta, :left, :bottom, delta=delta/2)
       point(r1, y1, "大円:r1,(r1,y1)", :red, :center, delta=-delta/2)
       point(r2, r2, "小円:r2\n(r2,r2)", :green, :center, :bottom, delta=delta)
   end
end;

算額（その1147）

算額（その1147）

一〇八 加須市騎西町 玉敷神社 大正4年(1915)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：正三角形，正方形

交差する大小の正三角形の中に 3 個の正方形を容れる。大きい正三角形の一辺の長さが 10 寸のとき，正方形の一辺の長さはいかほどか。

大きい正三角形の一辺の長さを 2a
正方形の一辺の長さを 2b
下にある正方形の左右の頂点を通る，大きい正三角形の斜辺と並行な直線が作る正三角形は上にある正方形を内包する正三角形と合同である。下に新たに作った正三角形の底辺の長さを 2c とおく。
eq1 は b, c のみを含む関係式，eq2 は a, b, c を含む関係式である。両者を併せて b, c を求めれば，それぞれは a のみを含む式になる。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, c::positive
eq1 = 2b/(c - b) - √Sym(3)
eq2 = ((√Sym(3)a - 2b)/√Sym(3))/2 - c;

res = solve([eq1, eq2], (b, c));
res[b] |> simplify |> println
res[c] |> simplify |> println

   a*(-1 + sqrt(3))/4
   a*(sqrt(3) + 3)/12

正方形の一辺の長さは，大正三角形の一辺の長さの (-1 + sqrt(3))/4 倍である。
大正三角形の一辺の長さが 10 寸のとき，正方形の一辺の長さは 1.830127018922193 寸である。

function draw(a, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   s3 = √3
   b = a*(s3 - 1)/4
   c = a*(s3 + 3)/12
   @printf("大正三角形の一辺の長さが %g のとき，正方形の一辺の長さは %g である。\n", 2a, 2b)
   plot([a, 0, -a, a], [0, s3*a, 0, 0], color=:blue, lw=0.5)
   y = s3*a
   x = (y - 2b)/s3
   plot!([x, 0, -x, x], [y, 2b, y, y], color=:green, lw=0.5)
   rect(-b, 0, b, 2b, :red)
   rect(c - b, y - 2b, c + b, y, :red)
   rect(b - c, y - 2b, -b -c, y, :red)
   segment(c, 0, 0, s3*c, :gray80)
   segment(-c, 0, 0, s3*c, :gray80)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(b, 0, " b", :red, :left, :bottom, delta=delta/2)
       point(c, 0, " c", :black, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, 2b, " 2b", :red, :left, delta=-delta/2)
       point(0, s3*c, " √3c", :black, :left, :vcenter)
       point(0, s3*a, "√3a", :blue, :center, :bottom, delta=delta/2)
       point(c, s3*a, "(c,√3a)", :blue, :center, :bottom, delta=delta/2)
       point(2c, s3*a, "(2c,√3a)", :blue, :center, :bottom, delta=delta/2)
       point(c + b, s3*a - 2b, "(c+b,√3a-2b)", :red, :left, delta=-delta)
   end
end;

算額（その1146）

算額（その1146）

一〇四 北足立郡桶川町加納 氷川天満神社 明治43年(1910)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円2個，直角三角形，正方形

直角三角形の中に正方形と 2 個の円を容れる。鈎，股が 3 寸，4 寸のとき，正方形の一辺の長さと円の直径を求めよ。

正方形の一辺の長さを a，円の直径を r とおき，以下の方程式を解く。

include("julia-source.txt")

using SymPy

@syms 鈎::positive, 股::positive, a::positive, r::positive
eq1 = (鈎 - a)/a - 鈎/股
eq2 = 2a - sqrt(2a^2) - 2r;

まず，正方形の一辺の長さを求める。

a = 股*鈎/(股 + 鈎) で，鈎，股が 3 寸, 4 寸のとき，正方形の一辺の長さは 1.71428571428571 寸である。

ans_a = solve(eq1, a)[1]
ans_a |> println
ans_a(鈎 => 3, 股 => 4).evalf() |>println

   股*鈎/(股 + 鈎)
   1.71428571428571

eq2 の a に代入し，方程式を解き r を求める。

r = -鈎*(sqrt(2)*股*sqrt(股^2/(股 + 鈎)^2) - 2*股 + sqrt(2)*鈎*sqrt(股^2/(股 + 鈎)^2))/(2*股 + 2*鈎) で，鈎，股が 3 寸, 4 寸のとき，円の直径は 1.00420532164612 寸である。

eq2 = eq2(a => ans_a);
ans_r = solve(eq2, r)[1] |> simplify
ans_r |> println
2ans_r(鈎 => 3, 股 => 4).evalf() |>println

   -鈎*(sqrt(2)*股*sqrt(股^2/(股 + 鈎)^2) - 2*股 + sqrt(2)*鈎*sqrt(股^2/(股 + 鈎)^2))/(2*股 + 2*鈎)
   1.00420532164612

function draw(鈎, 股, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 股*鈎/(股 + 鈎)
   r = -鈎*(sqrt(2)*股*sqrt(股^2/(股 + 鈎)^2) - 2*股 + sqrt(2)*鈎*sqrt(股^2/(股 + 鈎)^2))/(2*股 + 2*鈎)
   @printf("鈎，股が %g，%g のとき，正方形の一辺の長さは %g，円の直径は %g である。\n", 鈎, 股, a, 2r)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   plot!([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
   segment(0, a, a, 0, :magenta)
   circle(r, r, r)
   circle(a - r, a - r, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(股, 0, " 股", :blue, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, 鈎, " 鈎", :blue, :left, :bottom, delta=delta/2)
       point(0, a, " a", :blue, :left, :bottom, delta=delta/2)
       point(r, r, "(r, r)", :red, :center, delta=-delta/2)
   end
end;