算額（その1152）

算額（その1152）

　九九 春日部市小渕 観音院 明治30年(1897)
一〇三 春日部市 東福寺 明治40年(1907)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：正五角形，正方形，五角法

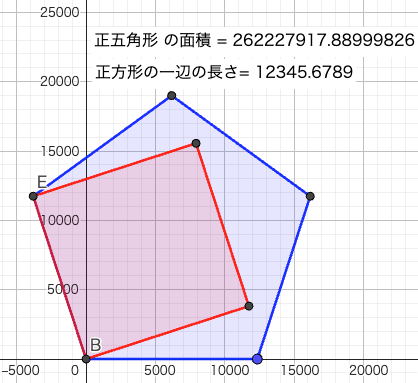
面積が 262155154.5032769612 坪の正五角形の土地の一辺の長さはいかほどか。

以下の図は GeoGebra で，一辺を与えた正多角形をかき，その面積を求めたものである。算額の「答」を得るために，「問」の数値を変えている。

注：10間四方=1坪

正五角形の一辺の長さを a，一辺の両端と正五角形の中心を結ぶ二等辺三角形の高さを h とする。
h = a/2/tand(Sym(72)/2) で，正五角形の面積は，5 * a*h/2 = 5 * (a * (a/2)/tand(72/2))/2 である。

include("julia-source.txt")

using SymPy

@syms S::positive, a::positive

S = 5 * a*h/2
S |> println

   5*a^2/(4*sqrt(5 - 2*sqrt(5)))

a^2 にかかる係数 5/(4*sqrt(5 - 2*sqrt(5))) = 1.7204774005889671 を「五角法」と呼ぶ。

5/(4*sqrt(5 - 2*sqrt(5)))

   1.7204774005889671

慣例的に，五角法の近似値として 1.72 が使われていた。その場合，正五角形の面積は S = 1.72*a^2 となる。a について解けば a = sqrt(S/1.72) である。

与えられた条件は，正五角形の面積が 262155154.5032769612 なので，正五角形の一辺の長さは sqrt(262155154.5032769612/1.72) = 12345.6789 = 123456.789 間である。
この「きれいな結果」を出すために，あのとんでもない長い数字列の面積が与えられたのだ。

sqrt(262155154.5032769612/1.72) |> println
sqrt(big"262155154.5032769612"/big"1.72") |> println

   12345.6789
   12345.67890000000000000000000000000000000000000000000000000000000000000000000004

しかし，近似値でない五角法を使えば，「きれいな数値は出てこない」

sqrt(262155154.5032769612/1.7204774005889671) |> println
sqrt(big"262155154.5032769612"/big"1.7204774005889671") |> println

   12343.96593263111
   12343.96593263111017155386297511751038450862787310648018338764402293502103615974

最初の図に示したが，正確な五角法を使うときには，「正五角形の面積は 262227917.89 坪」といえばよい。そうすれば答えは 123456.789 間になる。

sqrt(big"262227917.89"/big"1.7204774005889671")

   12345.67890000004107475558293899828913755690970317874535819580788216955810780953

算額（その1151）

算額（その1151）

七八 加須市大字外野 棘脱地蔵堂 明治9年(1876)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円7個，最大値

交差する 2 個の大円の交差部分に中円 1 個，小円 2 個を容れる。大円の直径が 3.5 寸のとき，小円の最大直径はいかほどか。

注：交差する部分が小さければ小円も小さい。交差部分が大きくなるに連れ小円も大きくなるが，ある点をすぎれば逆に小さくなる。なお，図には大円の内部にもう一個（二個）の円があるがそれは交差部分の大きさに連動するので解を得るには無関係である。

大円の半径と中心座標を r1, (0, r2)
中円の半径と中心座標を r3, (0, 0)
小円の半径と中心座標を r4, (r3 + r4, 0)
とおく。
ただし，今回の方程式 eq1 は，大円，中円，小円の中心が構成する直角三角形におけるピタゴラスの定理である。
大円の交差の程度は中円の半径 r3 により評価される。小円の半径は中円の半径により決まる。
eq1 を解いて r3 から r4 を求める式を得る。これを関数 f とする。r4 = f(x3)。

include("julia-source.txt")

using SymPy

@syms r1::positive, x1::positive, r2::positive, r3::positive, r4::positive
r1 = 35//20
eq1 = (r1 - r3)^2 + (r3 + r4)^2 - (r1 - r4)^2
f = solve(eq1, r4)[1]

using Plots
pyplot(size=(500, 200), grid=false, aspectratio=:none, label="")
plot(f, xlims=(0, 3.5/2), xlabel="r3", ylabel="r4")

図を描いてみると，r3 が 0.7 近辺で r4 が最大になるのがわかる。
r4 が最大になるときの r3 を求めるには，f の導関数 g を求め g(r3) = 0 を解けばよい。

g = diff(f, r3) |> simplify
g |> println

   (-16*r3^2 - 56*r3 + 49)/(16*r3^2 + 56*r3 + 49)

ans_r3 = solve(g, r3)[1] |> factor
ans_r3 |> println
ans_r3.evalf() |> println

   7*(-1 + sqrt(2))/4
   0.724873734152916

g(r3) = 0 の解 ans_r3 により f(ans_r3) がr4 の最大値である。

res = 2*f(ans_r3) |> simplify
res |> println
res.evalf() |> println

   21/2 - 7*sqrt(2)
   0.600505063388335

21/2 - 7*sqrt(2) は x1 = 3.5/2 のときの解なので，3.5/2 で割ってやれば一般解になる。直径を一般解とするなら 3.5 で割ればよい。

@syms r1
res/(35//10)*r1 |> println

   r1*(3 - 2*sqrt(2))

最大時の小円の直径は大円の直径の (3 - 2√2) 倍である。
大円の直径が 3.5 寸 のとき，小円の直径は 3.5*(3 - 2√2) = 0.600505063388334 寸である。

function draw(r1, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 7*(-1 + sqrt(2))/4
   r2 = r1 - r3
   r4 = r1*(3 - 2*sqrt(2))
   #@printf("正方形の一辺の長さが %g，大円の直径が %g のとき，小円の直径は %g である。\n", a, 2r1, 2r2)
   plot()
   circle22(0, r2, r1)
   circle22(0, r2 + r1 - r2, r2, :blue)
   circle(0, 0, r3, :green)
   circle2(r3 + r4, 0, r4, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r2, "大円:r1,(0,r2)", :red, :center, :bottom, delta=delta/2)
       point(0, r1, "", :blue)
       point(0, 0, "中円:r3,(0,0)", :green, :center, :bottom, delta=delta/2)
       point(r3 + r4, 0, "小円:r4,(r3＋r4,0)", :black, :center, delta=-delta/2)
   end
end;

算額（その1150）

算額（その1150）

五七 羽生市小松 小松神社 安政6年()
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円2個，楕円，正六角形2個

楕円の中に 2 個の等円と 2 個の正六角形を容れる。等円の直径が 1 寸のとき，正六角形の一辺の長さはいかほどか。

正六角形の一辺の長さを 2a
楕円の長半径と短半径を 4a, b
等円の半径と中心座標を r, (0, b - r)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, r::positive
eq1 = dist2(0, 0, a, √Sym(3)a, 0, b - r, r)
eq2 = (3a)^2/(4a)^2 + (√Sym(3)a)^2/b^2 - 1
res = solve([eq1, eq2], (a, b))[1]

   (sqrt(21)*r/4, 3*r)

正六角形の一辺の長さは r*√21/2 である。

2res[1](r => 10/2).evalf() |> println

   11.4564392373896

function draw(r, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (sqrt(21)*r/4, 3*r)
   #@printf("正方形の一辺の長さが %g，大円の直径が %g のとき，小円の直径は %g である。\n", a, 2r1, 2r2)
   #x = a.*[0, 1, 3, 4, 3, 1, 0]
   #y = a.*[0, √3, √3, 0, -√3, -√3, 0]
   #plot(x, y, color=:blue, lw=0.5)
   #plot!(x .- 4a, y, color=:blue, lw=0.5)
   plot(a.*[4, 3, 1, -1, -3, -4, -3, -1, 1, 3, 4],
       √3a.*[0, -1, -1, 1, 1, 0, -1, -1, 1, 1, 0], color=:blue, lw=0.5)
   circle22(0, b - r, r)
   ellipse(0, 0, 4a, b, color=:green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(4a, 0, " 4a", :blue, :left, :bottom, delta=delta/2)
       point(3a, √3a, "(3a,√3a)", :blue, :left, :bottom, delta=delta/2)
       point(a, √3a, "(a,√3a)", :blue, :left, :bottom, delta=delta/2)
       point(0, b, "b", :green, :center, :bottom, delta=delta)
       point(0, b - r, " b-r", :red, :left, :vcenter)
       dimension_line(a, √3a - 2delta, 3a, √3a - 2delta, "2a", delta=-2delta)
   end
end;