算額（その1128）

算額（その1128）

四十四 岩手県一関市真滝 熊野白山滝神社 文久元年(1861)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円5個，直線

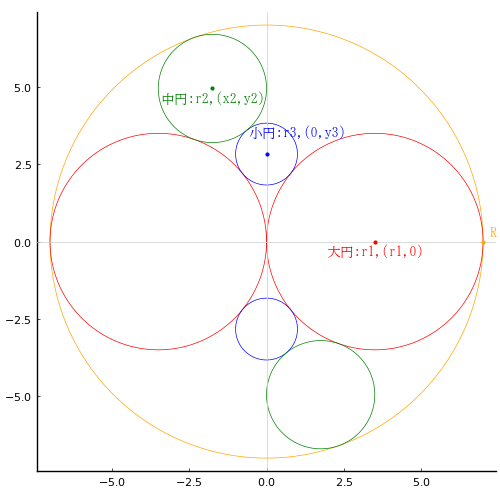
互いに接している大円と中円があり，両者を通る直線と各円の隙間に 3 個の小円を容れる。大円と小円の直径が 10 寸，1 寸のとき，中円の直径はいかほどか。

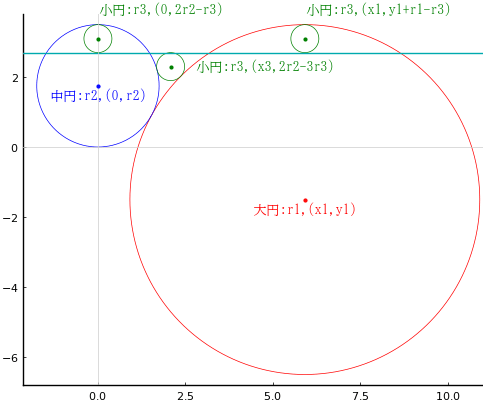
大円の半径と中心座標を r1, (x1, y1)
中円の半径と中心座標を r2, (0, r2)
小円の半径と中心座標を r3, (0, 2r2 - r3), (x3, 2r2 - 3r3), (x1, y1 + r1 - r3)
とおき，以下の連立方程式を解く。

注：大円と小円の直径が 10 寸，1 寸のとき，y1 = 0 となるが，これは特殊な場合で常に y1 = 0 が成り立つわけではない。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive, x1::positive, y1,
     r2::positive, x2::positive, y2::positive,
     r3::positive, x3::positive;
y1 = 2r2 - r1
eq1 = (x1 - x3)^2 + (2r2 - 3r3 - y1)^2 - (r1 + r3)^2
eq2 = x3^2 + (r2 - 3r3)^2 - (r2 + r3)^2
eq3 = x1^2 + (r2 - y1)^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3], (r2, x1, x3))[4]  # 4 of 4

   (2*r1*(r1^3*r3 + 2*r1^2*r3^(3/2)*sqrt(r1 - r3) - 4*r1^2*r3^2 - 8*r1*r3^(5/2)*sqrt(r1 - r3) + 4*r1*r3^3 + 8*r3^(7/2)*sqrt(r1 - r3))/(r1^4 - 8*r1^3*r3 + 24*r1^2*r3^2 - 32*r1*r3^3 + 16*r3^4), 2*sqrt(2)*r1*sqrt((r1^4*r3^2 + 4*r1^3*r3^(5/2)*sqrt(r1 - r3) - 16*r1^2*r3^(7/2)*sqrt(r1 - r3) - 16*r1^2*r3^4 + 16*r1*r3^(9/2)*sqrt(r1 - r3) + 32*r1*r3^5 - 16*r3^6)/(r1^4 - 8*r1^3*r3 + 24*r1^2*r3^2 - 32*r1*r3^3 + 16*r3^4))*(r1^4*r3^(5/2)*sqrt(r1 - r3) - r1^4*r3^3 - 8*r1^3*r3^(7/2)*sqrt(r1 - r3) + 8*r1^3*r3^4 + 24*r1^2*r3^(9/2)*sqrt(r1 - r3) - 24*r1^2*r3^5 - 32*r1*r3^(11/2)*sqrt(r1 - r3) + 32*r1*r3^6 + 16*r3^(13/2)*sqrt(r1 - r3) - 16*r3^7)/(r3^3*(r1^5 - 10*r1^4*r3 + 40*r1^3*r3^2 - 80*r1^2*r3^3 + 80*r1*r3^4 - 32*r3^5)), 2*sqrt(2)*sqrt((r1^4*r3^2 + 4*r1^3*r3^(5/2)*sqrt(r1 - r3) - 16*r1^2*r3^(7/2)*sqrt(r1 - r3) - 16*r1^2*r3^4 + 16*r1*r3^(9/2)*sqrt(r1 - r3) + 32*r1*r3^5 - 16*r3^6)/(r1^4 - 8*r1^3*r3 + 24*r1^2*r3^2 - 32*r1*r3^3 + 16*r3^4)))

かなり複雑な式で分母は因数分解できるも場合もあるが(r2, x1)，分子を含めると式は簡単にはできない。術にもあるが，簡単な式にできたと思っても，それは特定の条件下のものに過ぎないと思われる。

大円と小円の直径が 10 寸，1 寸のとき，中円の直径は 5 寸である（r2 = 2.5）。

res[1](r1 =>10/2, r3 => 1/2).evalf() |> println
res[2](r1 =>10/2, r3 => 1/2).evalf() |> println
res[3](r1 =>10/2, r3 => 1/2).evalf() |> println

   2.50000000000000
   7.07106781186548
   2.82842712474619

術では 「+ 0.5」 とあるのを山村が 「- 0.1」 と訂正した。確かにそのようにすれば中円の直径として 5 が得られる。
しかし，これは「大円径 = 10，小円径 = 1」のときのみの付け焼き刃に過ぎず，一般解ではない。

大円径 = 10
小円径 = 1
A = (大円径 - 小円径)*小円径
B = √A/大円径 - 0.1  # 
中円径 = 小円径/B

   5.0

たとえば，大円径が 10，小円径が 0.8 のときの計算をすると破綻が露見する。
正しい答えは，「大円の直径が 10， 小円の直径が 0.8 のとき，中円の直径は 3.49792834161003」である。

その他のパラメータは以下の通りである。
r1 = 5;  r3 = 0.4;  r2 = 1.74896;  x1 = 5.91433;  x3 = 2.07766

2res[1](r1 =>10/2, r3 => 0.8/2).evalf() |> println

   3.49792834161003

山村の訂正では，中円の半径は 4.670354708490701 になる。どちらが正しいかは，図を見ればわかる。

大円径 = 10
小円径 = 0.8
A = (大円径 - 小円径)*小円径
B = √A/大円径 - 0.1  # 
中円径 = 小円径/B

   4.670354708490701

function draw(r1, r3, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   t = sqrt(r1 - r3)
   r2 = 2*r1*(r1^3*r3 + 2*r1^2*r3^(3/2)*t - 4*r1^2*r3^2 - 8*r1*r3^(5/2)*t + 4*r1*r3^3 + 8*r3^(7/2)*t)/(r1 - 2*r3)^4
   x3 = 2*sqrt(2)*sqrt((r1^4*r3^2 + 4*r1^3*r3^(5/2)*t - 16*r1^2*r3^(7/2)*t - 16*r1^2*r3^4 + 16*r1*r3^(9/2)*t + 32*r1*r3^5 - 16*r3^6)/(r1^4 - 8*r1^3*r3 + 24*r1^2*r3^2 - 32*r1*r3^3 + 16*r3^4))
   x1 = r1*x3*(r1^4*r3^(5/2)*t - r1^4*r3^3 - 8*r1^3*r3^(7/2)*t + 8*r1^3*r3^4 + 24*r1^2*r3^(9/2)*t - 24*r1^2*r3^5 - 32*r1*r3^(11/2)*t + 32*r1*r3^6 + 16*r3^(13/2)*t - 16*r3^7)/(r3^3*(r1 - 2*r3)^5)
   y1 = 2r2 - r1
   @printf("大円の直径が %g， 小円の直径が %g のとき，中円の直径は %g である。\n", 2r1, 2r3, 2r2)
   @printf("r1 = %g;  r3 = %g;  r2 = %g;  x1 = %g;  x3 = %g\n", r1, r3, r2, x1, x3)
   plot()
   circle(x1, y1, r1)
   circle(0, r2, r2, :blue)
   circle(0, 2r2 - r3, r3, :green)
   circle(x3, 2r2 - 3r3, r3, :green)
   circle(x1, y1 + r1 - r3, r3, :green)
   hline!([2r2 - 2r3])
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, y1, "大円:r1,(x1,y1)", :red, :center, delta=-delta/2)
       point(0, r2, "中円:r2,(0,r2)", :blue, :center, delta=-delta/2)
       point(0, 2r2 - r3, "小円:r3,(0,2r2-r3)", :green, :left, :vcenter, delta=6delta)
       point(x3, 2r2 - 3r3, "小円:r3,(x3,2r2-3r3)", :green, :left, :vcenter, deltax=5delta)
       point(x1, y1 + r1 - r3, "小円:r3,(x1,y1+r1-r3)", :green, :left, :vcenter, delta=6delta)
   end
end;

算額（その1127）

算額（その1127）

四十四 岩手県一関市真滝 熊野白山滝神社 文久元年(1861)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円7個，外円

全円の中に大円，中円，小円をそれぞれ 2 個ずつ容れる。大円，小円の直径がそれぞれ 7 寸，2 寸のとき，中円の直径はいかほどか。

山村の図は，意地悪としか思えないほど実際の姿と異なっている。山村の図が正しいものとして解こうとしても解は得られない。

全円の半径と中心座標を R, (0, 0); R = 2r1
大円の半径と中心座標を r1, (r1, 0)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (0, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive, r2::positive, x2::positive, y2::positive,
     r3::positive, y3::positive;
R = 2r1
eq1 = r1^2 + y3^2 - (r1 + r3)^2
eq2 = x2^2 + y2^2 - (R - r2)^2
eq3 = x2^2 + (y2 - y3)^2 - (r2 + r3)^2
eq4 = (x2 + r1)^2 + y2^2 - (r1 + r2)^2
res = solve([eq1, eq2, eq3, eq4], (r2, x2, y2, y3))[1]

   (r1*(2*r1 + r3)/(2*r1 + 9*r3), r1*(2*r1 - 15*r3)/(2*r1 + 9*r3), 8*r1*sqrt(r3)*sqrt(2*r1 + r3)/(2*r1 + 9*r3), sqrt(r3)*sqrt(2*r1 + r3))

大円，小円の半径を r1, r3 としたとき，中円の半径 r2 は r1*(2*r1 + r3)/(2*r1 + 9*r3) である。

大円の直径が 7， 小円の直径が 2 のとき，中円の直径は 3.5 である。

その他のパラメータは以下の通りである。

   r1 = 3.5;  r3 = 1;  r2 = 1.75;  x2 = -1.75;  y2 = 4.94975;  y3 = 2.82843

function draw(r1, r3, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   s = 2r1 + r3
   t = 2r1 + 9r3
   r2 = r1*s/t
   x2 = r1*(2r1 - 15r3)/t
   y2 = 8r1*sqrt(r3*s)/t
   y3 = sqrt(r3*s)
   @printf("大円の直径が %g， 小円の直径が %g のとき，中円の直径は %g である。\n", 2r1, 2r3, 2r2)
   @printf("r1 = %g;  r3 = %g;  r2 = %g;  x2 = %g;  y2 = %g;  y3 = %g\n", r1, r3, r2, x2, y2, y3)
   plot()
   circle(0, 0, 2r1, :orange)
   circle2(r1, 0, r1)
   circle22(0, y3, r3, :blue)
   circle(x2, y2, r2, :green)
   circle(-x2, -y2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, 0, "大円:r1,(r1,0)", :red, :center, delta=-delta/2)
       point(x2, y2, "中円:r2,(x2,y2)", :green, :center, delta=-delta/2)
       point(0, y3, "小円:r3,(0,y3)", :blue, :center, :bottom, delta=2.5delta, deltax=5delta)
       point(2r1, 0, " R", :orange, :left, :bottom, delta=delta/2)
   end
end;

算額（その1126）

算額（その1126）

四十一 岩手県一関市牧沢 牧沢八幡神社 明治8年(1875)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円4個，二等辺三角形
#Julia, #SymPy, #算額, #和算

二等辺三角形の中に，甲円，乙円，丙円を容れる。甲円と丙円の直径がわかっているときに，乙円の直径を求めよ。

与えられるものと求めるものが違うが，図形としては 算額（その164）と同じである。

二等辺三角形の底辺の長さを 2x，高さを y
甲円の半径と中心座標を r1, (0, r1)
乙円の半径と中心座標を r2, (0, 2r1 + r2)
丙円の半径と中心座標を r3, (x3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, r3::positive, x3::positive, x::positive, y::positive;

eq1 = x3^2 + (r1 - r3)^2 - (r1 + r3)^2 |> simplify  # 黃円と赤円が外接する
eq2 = r2/(y - 2r1 - r2) - r1/(y - r1)
eq3 = x/sqrt(x^2 + y^2) - r1/(y - r1)
eq4 = r3*x - r1*(x - x3);  # 三角形の相似
res = solve([eq1, eq2, eq3, eq4], (r2, x3, x, y))[1];

ans_r2 = res[1] |> factor
ans_r2 |> println
ans_r2(r1 => 4/2, r3 => 1/2) * 2 |> println

   (r1 - r3)^2/(4*r3)
   2.25000000000000

甲円の直径が 4，丙円の直径が 1 のとき，乙円の直径は 2.25 である。

res[2] |> println
res[3] |> println
res[4] |> println

   2*sqrt(r1)*sqrt(r3)
   2*r1^(3/2)*sqrt(r3)/(r1 - r3)
   -8*r1^2*r3/(r1^2 - 6*r1*r3 + r3^2)

全てのパラメータは以下のとおりである。

    r1 = 2;  r2 = 1.125;  r3 = 0.5;  x3 = 2;  x = 2.6666666666666674;  y = 9.142857142857142

function draw(r1, r3, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = (r1 - r3)^2/(4*r3)
   x3 = 2sqrt(r1*r3)
   x  = 2r1^(3/2)*sqrt(r3)/(r1 - r3)
   y  = -8r1^2*r3/(r1^2 - 6r1*r3 + r3^2)
   @printf("甲円の直径が %g，丙円の直径が %g のとき，乙円の直径は %g である。\n", 2r1, 2r3, 2r2)
   @printf("r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  x = %g;  y = %g\n", r1, r2, r3, x3, x, y)
   plot([x, 0, -x, x], [0, y, 0, 0], color=1, lw=0.5)
   circle(0, r1, r1, :orange)
   circle(0, 2r1 + r2, r2, :black)
   circle2(x3, r3, r3)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, " r1", :orange, :left, :vcenter)
       point(0, 2r1 + r2, "2r1+r2", :black, :center, delta=-delta/2)
       point(x3, r3, "(x3,r3)", :red, :center, delta=-delta/2)
       point(x, 0, " x", :blue, :left, :bottom, delta=delta/2)
       point(0, y, " y", :blue, :left, :bottom, delta=delta/2)
   end
end;