算額(その1352)
九 群馬県群馬郡群馬町引間 妙見寺 寛政9年(1797)
群馬県和算研究会:群馬の算額,上武印刷株式会社,高崎市,1987年3月31日.
キーワード:正方形,4等分割
#Julia, #SymPy, #算額, #和算
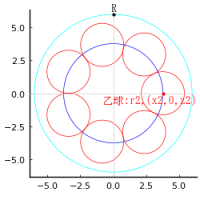
正方形の田んぼがある(45°回転)。図のように 3 本の割線で区切って,面積を 4 等分する。甲の長さはいかほどか。

正方形の一辺の長さを x
a, b, c を図のように定め,連立方程式を解く。
甲の長さは c - a + b である。
include("julia-source.txt");
using SymPy
@syms a::positive, b::positive, x::positive
c = x/√Sym(2)
eq1 = (c - b)^2 - x^2/4
eq2 = ((c - a) + (c - b - a)) * b/2 + (c - a)^2/2 - x^2/4
res = solve([eq1, eq2], (a, b))[1] # 1 of 4
(-x/2 + sqrt(2)*x - sqrt(-x^2 + (-x + 2*sqrt(2)*x)^2)/2, -x/2 + sqrt(2)*x/2)
a = -x/2 + sqrt(2)*x - sqrt(-x^2 + (-x + 2*sqrt(2)*x)^2)/2
b = -x/2 + sqrt(2)*x/2
甲の長さは正方形の一辺の長さの (x/sqrt(Sym(2)) - a + b) 倍である。
a, b を代入して,sqrt(2 - √2) 倍である。
甲 = (x/sqrt(Sym(2)) - a + b)
甲 = 甲(a => res[1], b => res[2]) |> simplify
甲 |> println
x*sqrt(2 - sqrt(2))
甲の長さは,正方形の一辺の長さの sqrt(2 - √2) 倍である。
正方形の一辺の長さが 10 寸のとき,甲は 10*sqrt(2 - √2) = 7.653668647301794 である。
x = 10
x*sqrt(2 - √2)
7.653668647301794
function draw(x, more)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
c = x/√2
(a, b) = (-x/2 + sqrt(2)*x - sqrt(-x^2 + (-x + 2*sqrt(2)*x)^2)/2, -x/2 + sqrt(2)*x/2)
甲 = sqrt(2 - √2)*x
@printf("正方形の一辺の長さが %g のとき,甲は %g\n", x, b + c - a)
println((a, b))
@printf("x = %g; a = %g; b = %g; c = %g\n", x, a, b, c)
plot([c, 0, -c, 0, c], [0, c, 0, -c, 0], color=:blue, lw=1)
segment(c - b, -b, b - c, -b, :red)
segment(a, -b, a, c - a, :red, lw=1)
segment(-a, -b, -a, c - a, :red)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(c - b, -b, " (c-b,-b)")
point(a, -b, "(a,-b)")
point(a, c - a, " (a,c-a)", :green, :left, :vcenter)
point(c, 0, " c", :green, :left, :vcenter)
point(0, c, "c", :green, :center, :bottom, delta=delta/2)
point(0, 0, " 0", :green, :left, :vcenter)
point(a, (c - a - b)/2, " 甲", :green, :left, :vcenter, mark=false)
end
end;
draw(10, true)