算額(その1426)
八十九 陸前高田市小友町 常膳寺観音堂 天保13年(1842)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:円4個,半円2個,四分円1個
#Julia, #SymPy, #算額, #和算
正方形の中に半円 2 個,四分円 1 個,大円 1 個,中円 2 個,小円 1 個を容れる。小円の直径が 1 寸のとき,中円の直径はいかほどか。
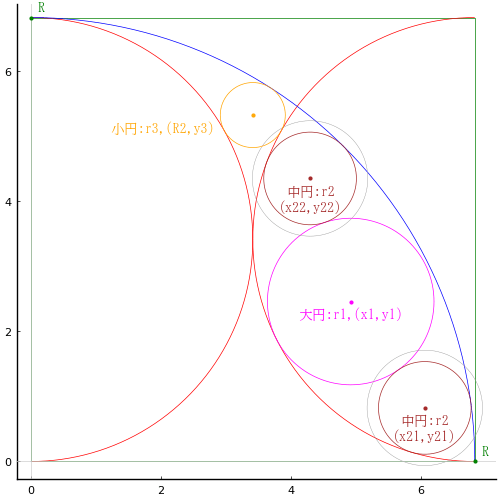
正方形の一辺の長さを R
四分円の半径を R
半円の半径を R/2
大円の半径と中心座標を r1, (x1, y1); y1 = x1/2
中円の半径と中心座標を r2, (x21, y21), (x22, y22)
小円の半径と中心座標を r3, (R/2, y3)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
@syms R::positive, r1::positive, x1::positive, y1::positive,
r2::positive, x21::positive, y21::positive,
x22::positive, y22::positive, r3::positive, y3::positive
R2 = R/2
y1 = x1/2
eq1 = R2^2 + y3^2 - (R - r3)^2
eq2 = R2^2 + (y3 - R2)^2 - (R2 + r3)^2
eq3 = (R - x1)^2 + (R2 - y1)^2 - (R2 - r1)^2
eq4 = (R - x21)^2 + (R2 - y21)^2 - (R2 - r2)^2
eq5 = (R - x22)^2 + (R2 - y22)^2 - (R2 - r2)^2
eq6 = x21^2 + y21^2 - (R - r2)^2
eq7 = x22^2 + y22^2 - (R - r2)^2
eq8 = (x21 - x1)^2 + (y1 - y21)^2 - (r1 + r2)^2
eq9 = (x22 - x1)^2 + (y1 - y22)^2 - (r1 + r2)^2;
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return Float64.(v), r.f_converged
end;
function H(u)
(R, r1, x1, r2, x21, y21, x22, y22, y3) = u
return [
R^2/4 + y3^2 - (R - r3)^2, # eq1
R^2/4 + (-R/2 + y3)^2 - (R/2 + r3)^2, # eq2
-(R/2 - r1)^2 + (R/2 - x1/2)^2 + (R - x1)^2, # eq3
-(R/2 - r2)^2 + (R/2 - y21)^2 + (R - x21)^2, # eq4
-(R/2 - r2)^2 + (R/2 - y22)^2 + (R - x22)^2, # eq5
x21^2 + y21^2 - (R - r2)^2, # eq6
x22^2 + y22^2 - (R - r2)^2, # eq7
-(r1 + r2)^2 + (-x1 + x21)^2 + (x1/2 - y21)^2, # eq8
-(r1 + r2)^2 + (-x1 + x22)^2 + (x1/2 - y22)^2, # eq9
]
end;
r3 = 1/2
iniv = BigFloat[6.8, 1.3, 4.9, 0.7, 6.1, 0.81, 4.3, 4.4, 5.3]
res = nls(H, ini=iniv)
([6.82842712474619, 1.2810685816644012, 4.920484251655344, 0.7126517245944497, 6.059977212374935, 0.8242481001480593, 4.2953848075434085, 4.353432909811113, 5.32842712474619], true)
小円の直径が 1 寸のとき,中円(茶色で示した円)の直径は 2r2 = 2*0.7033666754658107 = 1.4067333509316213 である。
算額の「答」,「術」による中円の直径は 1.775275591337676 寸である。この数値では,図に示した灰色の円になり,明らかに不適切である。
function draw(r3, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r1, x1, r2, x21, y21, x22, y22, y3) = [6.82842712474619, 1.2810685816644012, 4.920484251655344, 0.7126517245944497, 6.059977212374935, 0.8242481001480593, 4.2953848075434085, 4.353432909811113, 5.32842712474619]
R2 = R/2
y1 = x1/2
@printf("小円の直径が %g のとき,中円の直径は %.15g である。\n", 2r3, 2r2)
# @printf("r2 = %g; R = %g; r1 = %g; x1 = %g; x0 = %g; y0 = %g; y = %g\n", r2, R, r1, x1, x0, y0, y)
plot([0, R, R, 0, 0], [0, 0, R, R, 0], color=:green, lw=0.5)
circle(0, R2, R2, beginangle=-90, endangle=90)
circle(R, R2, R2, beginangle=90, endangle=270)
circle(0, 0, R, :blue, beginangle=0, endangle=90)
circle(x1, y1, r1, :magenta)
circle(x21, y21, r2, :brown)
circle(x22, y22, r2, :brown)
false_r2 = (√45 - 1) * (√3 + 2)/12/2
println("算額の「答」,「術」による不適切な中円径 = $(2false_r2)")
circle(x21, y21, false_r2, :gray60, lw=0.3)
circle(x22, y22, false_r2, :gray60, lw=0.3)
circle(R2, y3, r3, :orange)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) / 3 # size[2] * fontsize * 2
vline!([0], color=:gray80, lw=0.5)
hline!([0], color=:gray80, lw=0.5)
point(x1, y1, "大円:r1,(x1,y1)", :magenta, :center, delta=-delta)
point(x21, y21, "中円:r2\n(x21,y21)", :brown, :center, delta=-delta)
point(x22, y22, "中円:r2\n(x22,y22)", :brown, :center, delta=-delta)
point(R2, y3, "小円:r3,(R2,y3)", :orange, :right, delta=-delta, deltax=-6delta)
point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
point(0, R, " R", :green, :left, :bottom, delta=delta/2)
end
end;
draw(1/2, true)



























