算額（その1296）

算額（その1296）

六十四 群馬県安中市板鼻 鷹巣神社 天保11年(1840)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円10個，外円

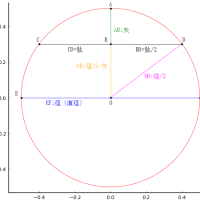
外円の中に甲乙丙丁戊の円を容れる。甲円，乙円の直径が 4 寸，9 寸のとき，外円の直径はいかほどか。
異版では，名前の付け方が違うが，本問に対応付けると「丙円の直径も求めよ」としている。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (r1, y1)
乙円の半径と中心座標を r2, (r2, y2)
丙円の半径と中心座標を r3, (0, y3)
丁円の半径と中心座標を r4, (x4, y4)
戊円の半径と中心座標を r5, (x5. y5)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, y1::positive,
     r2::positive, y2::negative, r3::positive, y3::positive,
     r4::positive, x4::positive, y4::positive,
     r5::positive, x5::positive, y5::positive;
eq1 = r1^2 + (y1 - y3)^2 - (r1 + r3)^2
eq2 = (x4 - r1)^2 + (y1 - y4)^2 - (r1 + r4)^2
eq3 = (x5 - r1)^2 + (y1 - y5)^2 - (r1 + r5)^2
eq4 = r2^2 + (y3 - y2)^2 - (r2 + r3)^2
eq5 = (r2 - x4)^2 + (y4 - y2)^2 - (r2 + r4)^2
eq6 = (x5 - r2)^2 + (y5 - y2)^2 - (r2 + r5)^2
eq7 = x4^2 + (y3 - y4)^2 - (r3 + r4)^2
eq8 = (x5 - x4)^2 + (y5 - y4)^2 - (r4 + r5)^2
eq9 = r1^2 + y1^2 - (R - r1)^2
eq10 = r2^2 + y2^2 - (R - r2)^2
eq11 = x5^2 + y5^2 - (R - r5)^2;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (R, y1, y2, r3, y3, r4, x4, y4, r5, x5, y5) = u
   return [
       r1^2 - (r1 + r3)^2 + (y1 - y3)^2,  # eq1
       (-r1 + x4)^2 - (r1 + r4)^2 + (y1 - y4)^2,  # eq2
       (-r1 + x5)^2 - (r1 + r5)^2 + (y1 - y5)^2,  # eq3
       r2^2 - (r2 + r3)^2 + (-y2 + y3)^2,  # eq4
       -(r2 + r4)^2 + (r2 - x4)^2 + (-y2 + y4)^2,  # eq5
       (-r2 + x5)^2 - (r2 + r5)^2 + (-y2 + y5)^2,  # eq6
       x4^2 - (r3 + r4)^2 + (y3 - y4)^2,  # eq7
       -(r4 + r5)^2 + (-x4 + x5)^2 + (-y4 + y5)^2,  # eq8
       r1^2 + y1^2 - (R - r1)^2,  # eq9
       r2^2 + y2^2 - (R - r2)^2,  # eq10
       x5^2 + y5^2 - (R - r5)^2,  # eq11
   ]
end;

(r1, r2) = (4/2, 9/2)
iniv = BigFloat[9.1, 6.9, -1.1, 1.9, 3.5, 0.94, 2.8, 4.0, 1.8, 5.3, 5.1]

res = nls(H, ini=iniv)

   ([9.142857142857142, 6.857142857142857, -1.1428571428571428, 1.9393939393939394, 3.463203463203463, 0.9411764705882353, 2.823529411764706, 4.033613445378151, 1.7777777777777777, 5.333333333333333, 5.079365079365079], true)

甲円，乙円の直径が 4 寸，9 寸のとき，外円の直径は 128/7 = 18 + 2/7 ≒ 18.2857 である。
丙円は 128/33 = 3 + 29/33 ≒ 3.87879 である。

すべてのパラメータは以下のとおりである。

   R = 9.14286;  y1 = 6.85714;  y2 = -1.14286;  r3 = 1.93939;  y3 = 3.4632;  r4 = 0.941176;  x4 = 2.82353;  y4 = 4.03361;  r5 = 1.77778;  x5 = 5.33333;  y5 = 5.07937

function draw(r1, r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, y1, y2, r3, y3, r4, x4, y4, r5, x5, y5) = [37.4/2, 12.9, -3.5, 7.9/2, 5.6, 2.3, 6.2, 5.9, 7.9/2, 12.2, 8.1]
   (R, y1, y2, r3, y3, r4, x4, y4, r5, x5, y5) = res[1]
   @printf("甲円，乙円の直径が %g, %g のとき，外円の直径は %g, 丙円の直径は %g である。\n", 2r1, 2r2, 2R, 2r3)
   @printf("R = %g;  y1 = %g;  y2 = %g;  r3 = %g;  y3 = %g;  r4 = %g;  x4 = %g;  y4 = %g;  r5 = %g;  x5 = %g;  y5 = %g\n", R, y1, y2, r3, y3, r4, x4, y4, r5, x5, y5)
   plot()
   circle(0, 0, R)
   circle2(r1, y1, r1, :blue)
   circle2(r2, y2, r2, :green)
   circle(0, y3, r3, :magenta)
   circle2(x4, y4, r4, :orange)
   circle2(x5, y5, r5, :brown)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, "R", :red, :center, :bottom, delta=delta/2)
       point(r1, y1, "甲円:r1\n(r1,y1)", :blue, :center, delta=-delta/2)
       point(r2, y2, "乙円:r2,(r2,y2)", :green, :center, delta=-delta/2)
       point(0, y3, "丙円:r3\n(0,y3)", :magenta, :center, delta=-delta/2)
       point(x4, y4, "丁円:r4,(x4,y4)", :black, :left, :bottom, delta=delta/2, deltax=-2delta)
       point(x5, y5, "戊円:r5\n(x5,y5)", :brown, :center, :bottom, delta=delta/2)
   end  
end;

draw(4/2, 9/2, true)

 

#和算