算額(その1447)
十一 金ケ崎町 個人宅 元文6年(1741)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
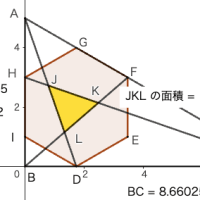
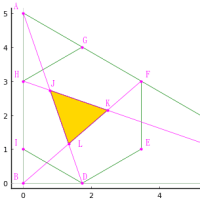
キーワード:正方形3個,円1個,直角三角形1個
#Julia, #SymPy, #算額, #和算
ごちゃごちゃしているので,分かりやすく書き下すと,以下の 6 式が述べられている。
(1) 「中正方形の面積から直角三角形の面積を除いたもの」と,「大正方形から円の面積を除いたもの」と,「小正方形の一辺の長さの 4 乗」を加えると 4240.36
(2) 鈎,股,円径を加えると 18
(3) 矢は 3
(4) 股 - 股 = 2
(5) 大方面 - 中方面 = 1
(6) 中方面 - 小方面 = 1
ただし,円積率として 0.79 ≒ π/4 = 0.7853981633974483 を使え。

注1:直径が5の円の面積は 5^2*0.79 = 19.75 と計算する。正確には π*2.5^2 = 19.634954084936208
以上 (1) 〜 (6) を連立方程式として解く。
using SymPy
@syms 大方面, 中方面, 小方面, 円径, 矢, 鈎, 股
矢 = 3
eq1 = (中方面^2 - 鈎*股/2) + (大方面^2 - 円径^2*0.79) + 小方面^4 - 4240.36
eq2 = 鈎 + 股 + 円径 - 18
eq3 = 円径 - (大方面 - 2矢)
eq4 = (股 - 鈎) - 2
eq5 = (大方面 - 中方面) - 1
eq6 = (中方面 - 小方面) - 1
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (大方面, 中方面, 小方面, 円径, 鈎, 股))[2] # 2 of 4
(10.0000000000000, 9.00000000000000, 8.00000000000000, 4.00000000000000, 6.00000000000000, 8.00000000000000)
すべて整数の解が得られた。中正方形の一辺の長さ(中方面)は 9 である。
eq2 〜 eq6 を連立方程式として大方面,小方面,円径,鈎,股を求めると以下のようになる。
res2 = solve([eq2, eq3, eq4, eq5, eq6], (大方面, 小方面, 円径, 鈎, 股))

この結果を eq1 に代入して,中方面のみを含む多項式にする。
eq1 = eq1(円径 => res2[円径], 鈎 => res2[鈎],大方面 => res2[大方面], 股 => res2[股], 小方面 => res2[小方面])
eq1 |> println
中方面^2 - (21/2 - 中方面/2)*(25/2 - 中方面/2)/2 - 0.79*(中方面 - 5)^2 + (中方面 - 1)^4 + (中方面 + 1)^2 - 4240.36
簡約化すると以下のように,中方面の 4 次式になるのでこれを解いて中方面を求める。
eq1 = eq1 |> simplify
eq1 |> println
1.0*中方面^4 - 4.0*中方面^3 + 7.085*中方面^2 + 11.65*中方面 - 4323.735
解は 4 個得られるが,そのうちの 2 個は虚数解,もう 1 つは不適切解であり,残りの 1 つのみが適解である。
中正方形の一辺の長さ(中方面)は 9 である。
solve(eq1)[2] |> println
9.00000000000000