算額(その1562)
七十一 岩手県一関市川崎町薄衣諏訪前 浪分神社 明治35年(1902)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード:球4個,円錐1個,四角柱1個
#Julia, #SymPy, #算額, #和算
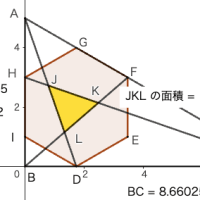
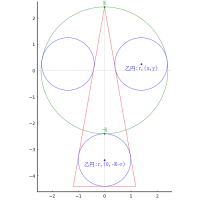
底面が正方形の四角柱の中に等球 4 個と円錐 1 個を容れる。円錐と四角柱の高さは等しい。等球は 2 個の等球と外接し,円錐と 1 点で外接し,四角柱に 3 点で内接する。等球の直径が与えられたとき,円錐(四角柱)の高さはいかほどか。
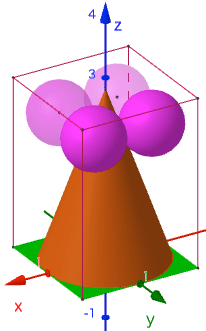
円錐の底面の半径と中心座標を a, (0, 0, 0)
四角柱の底面の座標を (a, a, 0), (a, -a, 0), (-a, a, 0), (-a, -a, 0)
等球の半径と中心座標を r, (a - r, a - r, h - r); a = 2r
とおき,以下の連立方程式を解く。
include("julia-source.txt")
# julia-source.txt ソース https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf
using SymPy
using LinearAlgebra
function shortest_distance_to_line(p0, p1, p2)
"""
点 p0 から p1, p2 を通る直線までの垂直距離を計算
"""
line_dir = p2 - p1 # 直線の方向ベクトル
numerator = norm(cross(line_dir, p0 - p1)) # 外積の大きさ
denominator = norm(line_dir) # 直線の方向ベクトルの大きさ
return numerator / denominator
end;
@syms a::positive, h::positive, r::positive
a = 2r
eq = shortest_distance_to_line([a - r, a - r, h - r], [a/√Sym(2), a/√Sym(2), 0], [0, 0, h]) - r
eq |> println
-r + sqrt(2)*Abs(h*(-sqrt(2)*r + r) + sqrt(2)*r*(h - r))/sqrt(h^2 + 4*r^2)
ans_h = solve(eq, h)[1]
ans_h |> println
4*sqrt(2)*r
円錐の高さ h は,等円の半径 r の 4√2 倍である。
等円の直径が 1 寸のとき,円錐の高さは 2√2 = 2.82842712474619 寸である。