算額(その1525)
三十一 一関市舞川 観福寺内地蔵堂前額 明治34年(1901)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
今有如図 03085
https://w.atwiki.jp/sangaku/pages/157.html
キーワード:正五角形,折り紙
#Julia, #SymPy, #算額, #和算
内部に正五角形の空白(DGFHI)ができるように細長い長方形の紙を折る。紙の幅 AD が与えられたとき,長さを求める術を述べよ。
山村の図は不正確極まりない。実際に紙を折ってみたり,算額を解いてみたりしていないというのが透けて見える。
「今有如図」も細かいところは不正確である。折り紙をしたらどうなるかを理解していないから,直角であるところが直角でないし,線を延長すると通るべき所を通っていない。
正確な図は以下のようになる。赤が表,ベージュは裏
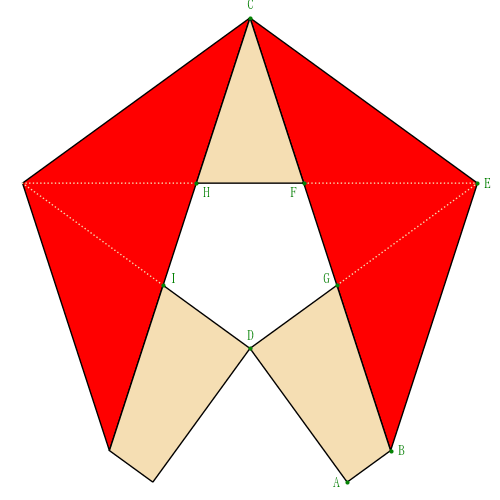
B, E の座標を (bx, by), (ex, ey)
B, E, C を円周上に持つ円の半径を R
D, G, F を円周上に持つ円の半径を r
とおき,BD の長さを求める。この時点では BD は R の関数である。
include("julia-source.txt");
using SymPy
@syms R::positive, r::positive
s18 = Sym(18)
s36 = Sym(36)
(ex, ey) = (R*cosd(s18), R*sind(s18))
(bx, by) = (R*sind(s36), -R*cosd(s36))
r = R*sind(s18)/cosd(s36)
BD = sqrt(bx^2 + (-r - by)^2) |> factor
BD |> println
R*sqrt(160 - 32*sqrt(5))/(4*(1 + sqrt(5)))
紙の長さは 2(AB + BC) である。
AB = BD*sind(s18) |> simplify;
BC = sqrt((R - by)^2 + bx^2) |> simplify;
長さ = 2(AB + BC) |> simplify
長さ |> println
R*(-sqrt(50 - 10*sqrt(5)) + 3*sqrt(10 - 2*sqrt(5)) + 4*sqrt(2*sqrt(5) + 10))/4
長さが R の関数として求められた。問は,長さを AD で表せということなので, R と AD の関係式を求める。
紙の幅 AD は BD*cosd(s18) である。
@syms AD
eq1 = AD - BD*cosd(s18)
eq1 |> println
AD - R*sqrt(160 - 32*sqrt(5))*sqrt(sqrt(5)/8 + 5/8)/(4*(1 + sqrt(5)))
方程式 eq1 を解いて R が AD でどのように表されるかを見る。
R = AD*(sqrt(5) + 5)/5 である。
ans_R = solve(eq1, R)[1]
ans_R |> println
AD*(sqrt(5) + 5)/5
長さを AD の関数で表す。
長さAD = 長さ(R => ans_R) |> sympy.sqrtdenest |> factor
長さAD |> println
-AD*(-10*sqrt(2)*sqrt(sqrt(5) + 5) - 2*sqrt(10)*sqrt(sqrt(5) + 5) - 5*sqrt(2)*sqrt(5 - sqrt(5)) + sqrt(10)*sqrt(5 - sqrt(5)))/10
紙の幅 AD = 10 のときの紙の長さは 61.5536707435051 である。
長さAD(AD => 10).evalf() |> println
61.5536707435051
「術」は 「紙の長さ = 2sqrt(sqrt(20) + 5) * 紙の幅」である。
2sqrt(sqrt(20) + 5) * 10 = 61.55367074350507 と,上の解と一致した。
「長さAD」は SymPy では簡約化できないが,「長さAD/AD」と術の「2sqrt(sqrt(20) + 5)」の差を取ると,ほぼゼロで,見かけの数式では同じように見えないが,両者は数値的に等しいことがわかる。
(長さAD/AD - 2sqrt(sqrt(Sym(20)) + 5)).evalf() |> println
-0.e-123
function draw(AD, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
s18 = 18
s36 = 36
R = AD*(√5 + 5)/5
r = R*sind(s18)/cosd(s36)
(cx, cy) = (0, R)
(dx, dy) = (0, -r)
(ex, ey) = (R*cosd(s18), R*sind(s18))
(bx, by) = (R*sind(s36), -R*cosd(s36))
(ax, ay) = (AD*sind(s36), -AD*cosd(s36) - r)
(fx, fy) = (r*sind(s36), r*cosd(s36))
(gx, gy) = (r*cosd(s18), -r*sind(s18))
r = R*sind(s18)/cosd(s36)
plot(showaxis=false)
plot!([bx, ex, cx, bx], [by, ey, cy, by], seriestype=:shape, color=:red, fillcolor=:red)
plot!(-[bx, ex, cx, bx], [by, ey, cy, by], seriestype=:shape, color=:red, fillcolor=:red)
plot!([fx, cx, -fx, fx], [fy, cy, fy, fy], seriestype=:shape, color=:wheat, fillcolor=:wheat)
plot!([ax, bx, gx, dx, ax], [ay, by, gy, dy, ay], seriestype=:shape, color=:wheat, fillcolor=:wheat)
plot!(-[ax, bx, gx, dx, ax], [ay, by, gy, dy, ay], seriestype=:shape, color=:wheat, fillcolor=:wheat)
plot!([gx, ex, fx], [gy, ey, fy], linestyle=:dot, color=:wheat)
plot!(-[gx, ex, fx], [gy, ey, fy], linestyle=:dot, color=:wheat)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
# hline!([0], color=:gray80, lw=0.5)
# vline!([0], color=:gray80, lw=0.5)
point(ax, ay, "A ", :green, :right, :vcenter)
point(bx, by, " B", :green, :left, :vcenter)
point(cx, cy, "C", :green, :center, :bottom, delta=delta)
point(dx, dy, "D", :green, :center, :bottom, delta=delta)
point(ex, ey, " E", :green, :left, :vcenter)
point(fx, fy, "F ", :green, :right, delta=-delta/2)
point(gx, gy, "G ", :green, :right, :bottom)
point(-fx, fy, " H", :green, :left, delta=-delta/2)
point(-gx, gy, " I", :green, :left, :bottom)
end
end;
draw(10, true)