算額（その1092）

算額（その1092）

五十一 岩手県一関市西風 西風白山神社 明治18年(1885)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円2個，楕円1個，正三角形

正三角形の中に楕円 1 個と 2 個の等円を容れる。等円の直径が与えられるとき，楕円の長径を求めよ。

等円の半径と中心座標を r, (0, r), (0, 3r)
楕円の長半径と短半径を a, b; b = r
正三角形の一辺の長さを 2l
楕円と正三角形の辺の接点座標を (x0, y0)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms l::positive, r::positive, a::positive, x0::positive, y0::positive
b = r
eq1 = r/(√Sym(3)l- 3r) - 1//2
eq2 = x0^2/a^2 + (y0 - r)^2/b^2 - 1
eq3 = -b^2*x0/(a^2*(y0 - r)) + √Sym(3)
eq4 = y0/x0 - 1/√Sym(3)
res = solve([eq1, eq2, eq3, eq4], (l, a, x0, y0))[1]

   (5*sqrt(3)*r/3, sqrt(5)*r, 5*sqrt(3)*r/4, 5*r/4)

楕円の長半径 a は，等円の半径 r の √5 倍である。
等円の直径が 1 寸のとき，楕円の長径は √5 = 2.23606797749979 寸である。

その他のパラメータは以下のとおりである。

   r1 = 0.5;  l = 1.44338;  a = 1.11803;  x0 = 1.08253;  y0 = 0.625

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (l, a, x0, y0) = (5*sqrt(3)*r/3, sqrt(5)*r, 5*sqrt(3)*r/4, 5*r/4)
   @printf("等円の直径が %g のとき，楕円の長径は %g である。\n", 2r, 2a)
   @printf("r1 = %g;  l = %g;  a = %g;  x0 = %g;  y0 = %g\n", r, l, a, x0, y0)
   plot([l, 0, -l, l], [0, √3l, 0, 0], color=:blue, lw=0.5)
   ellipse(0, r, a, r, color= :green)
   circle(0, r, r)
   circle(0, 3r, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x0, y0, " (x0,y0)", :green, :left, :vcenter)
       point(0, r, "等円:r,(0,r)", :red, :center, delta=-delta/2)
       point(0, 3r, "等円:r,(0,3r)", :red, :center, delta=-delta/2)
       point(a, r, "(a,r) ", :green, :right, :vcenter)
       point(0, 2r, "2r = 2b", :green, :center, delta=-delta/2)
       point(l, 0, " l", :blue, :left, :bottom, delta=delta/2)
       point(0, √3l, " √3l", :blue, :left, :vcenter)
   end
end;

算額（その1091）

算額（その1091）

四十三 岩手県一関市真滝 熊野白山滝神社 弘化3年(1846)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円1個，四分円2個，正方形

正方形の中に四分円を 2 個，円を 1 個容れる。円の直径が与えられたときに黒積（灰色の部分の 2 倍）を求めよ。

正方形の一辺の長さを R，円の半径を r とおき，以下の方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r::positive
eq1 = (R/2)^2 + r^2 - (R - r)^2
res = solve(eq1, R)[1]
res[1] |> println

   8*r/3

正方形の一辺の長さは円の半径の 8/3 倍である。

黒積の半分（図の灰色の部分）は，
扇形 OAR の面積（半径　R の円の面積の 1/6 = πR^2/6）から，
⊿AOC の面積（√3R/2 * R/2 / 2 = √3R^2/8）と，
円の面積の半分（πr^2/2）を引いたものの，
2倍である。

r = 1/2 のとき，R = 4/3 となり，黒積は 0.30648601314366886 である。

r = 1/2
R = 4/3
2(pi*R^2/6 - R^2*√3/8 - pi*r^2/2)

   0.30648601314366886

術は，円径^2*1.5593 とあるが，おかしい?

(2r)^2*1.5593

   1.5593

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   R = 8r/3
   黒積 = 2(pi*R^2/6 - R^2*√3/8 - pi*r^2/2)
   @printf("円の直径が %g(正方形の一辺の長さが %g) のとき，黒積は %g である。\n", 2r, R, 黒積)
   θ = 0:0.1:60
   x = @. R*cosd(θ)
   y = @. R*sind(θ)
   append!(x, [R/2, R])
   append!(y, [0, 0])
   plot([0, R, R, 0, 0], [0, 0, R, R, 0], color=:blue, lw=0.5)
   plot!(x, y, seriestype=:shape, fillcolor=:gray80)
   circlef(R/2, r, r, :white, beginangle=-90, endangle=90)
   circle(0, 0, R, beginangle=0, endangle=90)
   circle(R, 0, R, beginangle=90, endangle=180)
   circle(R/2, r, r, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       segment(R/2, 0, R/2, √3R/2)
       segment(0, 0, R/2, √3R/2)
       point(R/2, √3R/2, "A", :black, :center, :bottom, delta=delta/2)
       point(R, 0, " R", :black, :left, :bottom, delta=delta/2)
       point(0, 0, "O ", :black, :right, :bottom, delta=delta/2)
       circle(0, 0, 0.05R,  :black, beginangle=0, endangle=60)
       circle(0, 0, 0.055R,  :black, beginangle=0, endangle=60)
       point(0.13R, 0.01R, "60°", :black, :right, :bottom, delta=delta/2, mark=false)
       point(R/2, r, " B", :black, :left, :vcenter)
       point(R/2, 0, " C", :black, :left, :bottom, delta=delta)
       plot!(xlims=(-3delta, R + 3delta))
   end
end;

 

モンテカルロ法で，解析解のチェック

 一辺の長さが R の正方形の中に，半径 R の四分円 2 個と，半径 r の円を描く。

四分円と円の隙間（緑の点が散らばっている領域）の面積をモンテカルロ法により求める。

1000000 個の点を打って，領域内に入った点の割合から面積を推定すると，0.172231*R^2 となった。解析解は 0.17239838239331384*R^2 だったので，解析解を導いた式は間違っていなさそうだ。

using Random, Distributions, StatsBase
R = 1
r = 3R/8
n = 1000000
x = rand(Uniform(0.5, 1.0), n)
y = rand(Uniform(0, 1.0), n)
z = @. (x^2 + y^2 < R^2) && ((x - R/2)^2 + (y - r)^2 > r^2)
2*(R^2/2 * mean(z))

   0.172231

算額（その1090）

算額（その1090）

四十三 岩手県一関市真滝 熊野白山滝神社 弘化3年(1846)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，二等辺三角形，正方形

正方形の中に二等辺三角形と等円 3 個を容れる。等円の直径が与えられたとき，正方形の一辺の長さを求めよ。

正方形の一辺の長さを a，
正方形の辺の上にある二等辺三角形の頂点座標を (b, 0), (a - b, 0)
等円の半径と中心座標を r, (r, r), (a - r, r), (a - r, a - r)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms a::positive, b::positive, r::positive
eq1 = a + b - sqrt(a^2 + b^2) - 2r
eq2 = 2(a - b) - sqrt(2(a - b)^2) - 2r
res = solve([eq1, eq2], (a, b))[1]

   (2*r*(-sqrt(2) + sqrt(26 - 16*sqrt(2)) + 2*sqrt(13 - 8*sqrt(2)))/(-2 - sqrt(2) + sqrt(2)*sqrt(13 - 8*sqrt(2)) + 2*sqrt(13 - 8*sqrt(2))), r*(-sqrt(2) + sqrt(26 - 16*sqrt(2)) + 2 + 2*sqrt(13 - 8*sqrt(2)))/2)

t = sqrt(13 - 8√2) とおいて，
正方形の一辺の長さ a は r*(6 + √2 + (2 + √2)t)/2
斜線と正方形の一辺の交点座標 b は r*(2 - √2 + (2 + √2)t)/2
である。

等円の半径が 1/2 寸のとき，正方形の一辺の長さは 2.9619546674751045 寸である。

r = 1/2
t = sqrt(13 - 8√2)
r*(6 + √2 + (2 + √2)t)/2

   2.9619546674751045

「術」も正しい。

等円径 = 1
位 = (√2 + 6)
(sqrt(4位 -10) + 位)*等円径/4

   2.961954667475105

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   t = sqrt(13 - 8√2)
   a = r*(6 + √2 + (2 + √2)t)/2
   b = r*(2 - √2 + (2 + √2)t)/2
   @printf("等円の直径が %g のとき，正方形の一辺の長さは %g である。\n", 2r, a)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
   plot!([0, b, a, 0], [a, 0, a - b, a], color=:green, lw=0.5)
   circle(r, r, r)
   circle(a - r, r, r)
   circle(a - r, a - r, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r, r, "等円:r,(r,r)", :red, :center, delta=-delta/2)
       point(a - r, r, "等円:r,(a-r,r)", :red, :center, delta=-delta/2)
       point(a - r, a - r, "等円:r,(a-rr,a-rr)", :red, :center, delta=-delta/2)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, a, " a", :blue, :left, :bottom, delta=delta/2)
       point(b, 0, "b ", :green, :right, :bottom, delta=delta/2)
       point(a, a - b, "(a,a-b)  ", :green, :right, :vcenter)
   end
end;

算額（その1089）

算額（その1089）

四十三 岩手県一関市真滝 熊野白山滝神社 弘化3年(1846)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：楕円2個（楕円3個），正六角形（正三角形）

正六角形の中に等楕円（同じ大きさの楕円）を 2 個容れる。楕円の長径，短径が与えられたとき正六角形の一辺の長さを求めよ。

注：多分もとの算額の図でもそうなのであろうが，山村の図では楕円の書き方がまずく，図形を正確に表現できていない。正しくは下図のように，楕円は互いに接し，それぞれは正六角形の 2 辺にも接している。
算額では楕円を 2 個としているが正六角形の中心を点対称として，3 個の楕円を考えるとわかりやすい。しかも，第 3 の楕円は長径，短径が水平，垂直なので，計算しやすい。以下では，第 3 の楕円について解く。

原点を 第 3 の楕円の中心に置く。
楕円の長半径，短半径を a, b
正六角形の一辺の長さを l
楕円同士の接点（符号は違うが正六角形の一辺との接点と同じ）の座標を (x0, y0)
とおき，以下の連立方程式を解く。
作図する際には，(x0, y0) は不要である。

include("julia-source.txt")

using SymPy
@syms a::positive, b::positive, l::positive,
     x0::positive, y0::positive
@syms a, b, l, x0, y0
eq1 = x0^2/a^2 + y0^2/b^2 - 1
eq2 = -b^2*x0/(a^2*y0) + 1/√Sym(3)
eq3 = √Sym(3)y0 - √Sym(3)l/2 + x0
res = solve([eq1, eq2, eq3], (l, x0, y0))[2];

l，x0，y0 は以下のように，少し簡約化できる。

(2√Sym(3)sqrt(a^2 + 3b^2)/3, a^2/sqrt(a^2 + 3b^2), √Sym(3)b^2/sqrt(a^2 + 3b^2));

たとえば，長半径 が 4 寸，短半径が 2 寸のとき，正六角形の一辺の長さは 6.110100926607786 寸である。

a = 4
b = 2
2√3sqrt(a^2 + 3b^2)/3

   6.110100926607786

術は「邪術」である。これでは答えは出ない。
たとえば，長径と短径がともに 1 である（これは，円である）ときに以下のように 0.8611513361757016 になる。

長径 = 1
短径 = 1
位 = 長径^2 + 短径^2
A = (sqrt(位^2 + 2長径^2*短径^2) + 位)/6
sqrt(A)

   0.8611513361757016

図を描いてみると正六角形の一辺の長さは 0.8611513361757016 ではないことが明らかである。
円の半径が 1/2 なので，正三角形の一辺の長さは 2 になる。更に，正六角形の一辺の長さは，正三角形の一辺の長さの半分の 2/√3 倍で 1.1547005383792515 になる。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b) = (4, 2)
   (l, x0, y0) = (2*sqrt(3)*sqrt(a^2 + 3*b^2)/3, a^2/sqrt(a^2 + 3*b^2), sqrt(3)*b^2/sqrt(a^2 + 3*b^2))
   @printf("l = %.15g;  x0 = %g;  y0 = %g\n", l, x0, y0)
   plot([√3l/2, 0, -√3l/2, √3l/2], [0, 3l/2, 0, 0], color=:blue, lw=0.5)
   plot!(l .* [0, √3/2, √3/2, 0, -√3/2, -√3/2, 0],
       l .* [-1/2, 0, 1, 3/2, 1, 0, -1/2], color=:green, lw=0.5)
   circle(0, l/2, l)
   ellipse(0, 0, a, b, color=:magenta)
   ellipse(l/2*cosd(30), l/2*sind(30) + l/2, a, b, φ=120, color=:magenta)
   ellipse(-l/2*cosd(30), l/2*sind(30) + l/2, a, b, φ=240, color=:magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "", :magenta)
       point(l/2*cosd(30), l/2*sind(30) + l/2, "", :magenta)
       point(-l/2*cosd(30), l/2*sind(30) + l/2, "", :magenta)
       point(0, b, "b", :magenta, :center, :bottom, delta=delta/2)
       point(a, 0, " a", :magenta, :left, :bottom)
   end
end;

算額（その1088）

算額（その1088）

四十一 岩手県一関市牧沢 牧沢八幡神社 明治8年(1875)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円6個，外円，正五角形，五芒星

正五角形の対角線を引き，区画された領域に甲円 1 個，乙円 5 個を容れる。乙円の直径が 4 寸のとき，甲円の直径はいかほどか。

正五角形が内接する円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, 0)
乙円の半径と中心座標を r2, (0, r1 + r2)
とし，以下のように逐次決定してゆく。

計算において，必要な角度がいくつか出てくる。その三角関数の値は無理数ではあるが，きれいな形で表現される。

include("julia-source.txt")

using SymPy
@syms R
s18 = Sym(18)
s36 = Sym(36);

1.　甲円の半径

甲円の半径 OB は五芒星の頂点（正五角形の頂点） A の y 座標値に等しい。
∠AOR は 18° である。
甲円の半径は R*(√5 - 1)/4 である。

r1 = y = R*sind(s18)
r1 |> println

   R*(-1/4 + sqrt(5)/4)

2.　乙円の半径

乙円の半径 BD は BC * tan(∠BCD) である。
BC は OB * tan(∠BOC) である。
ここで，∠BCD = ∠BOC = 36°である。
まとめると，乙円の半径は R*(7√5 - 15)/4 である。

OB = R*sind(s18)
r2 = OB*tand(s36)*tand(s36)
r2 |> simplify |> println

   R*(-15 + 7*sqrt(5))/4

3.　乙円の直径が既知のときの甲円の直径

甲円の直径は乙円の直径の r1/r2 = 1/(5 - 2√5) = 2√5/5 + 1 = 1.894427190999916 倍である。
乙円の直径が 4 寸のとき，甲円の直径は 7.577708763999664 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 1
   # r1 = OB = R*sind(18)
   # r2 = BD = OB*tand(36)*tand(36)
   r1 = R*(√5 - 1)/4
   r2 = R*(7√5 - 15)/4
   θ = 90:-72:-342
   x = R .* cosd.(θ)
   y = R .* sind.(θ)
   plot()
   circle(0, 0, R)
   for i in 1:5
       segment(x[i], y[i], x[i + 1], y[i + 1], :blue)
       segment(x[i], y[i], x[i + 2], y[i + 2], :green)
   end
   circle(0, 0, r1, :magenta)
   rotate(0, r1 + r2, r2, :brown, angle=72)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(0, r1, "B", :magenta, :center, delta=-delta/2)
       point(0, r1 + r2, " D", :brown, :left, :vcenter)
       point(0, r1 + r2, "乙円", :brown, :center, delta=4delta)
       point(0, 0, "O", :red, :center, delta=-delta/2)
       point(0, 0, "甲円", :red, :center, delta=-3delta)
       point(r1*tand(36), r1, "C", :green, :left, :bottom, delta=delta/2)
       point(R*cosd(18), r1, " A", :blue, :left, :vcenter)
   end
end;

算額（その1087）

算額（その1087）

二十六 一関市萩荘 赤萩観音寺 弘化4年(1847)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円3個，正三角形，二等辺三角形

正三角形と二等辺三角形が重なってできる領域に等円を 3 個容れる。等円の直径が 1 寸のとき正三角形の一辺の長さはいかほどか。

正三角形の一辺の長さを 2a
等円の半径と中心座標を r, (x, r), (0, -r)
二等辺三角形の底辺の頂点座標を (x0, -2r)
とおいて以下の連立方程式を解く。
しかし，SymPy では一度に解けない。さらに，eq1, eq3 から x，x0 を求めて eq2 に代入し，方程式を解くも，a = √3r/3 という不適切回しかでてこない。方程式のグラフを描くと a = √3 という解があるのを確認できるのに不思議だ。
解析解を諦めて数値解を求めると解は求まる。

しかし，ここでめげてはいけない。初心に帰って図に示すような補助線を描くと，答えが見えてくる。

できる正三角形は全て合同で，一辺の長さは内接円の直径の √3 倍である。
したがって，等円の直径が 1 寸のとき，元の正三角形の一辺の長さは 2√3 = 3.4641016151377544 寸である。

include("julia-source.txt")

using SymPy
@syms a::positive, r::positive, x::positive, x0::positive
eq1 = dist2(a, 0, 0,√Sym(3)a, x, r, r)/√Sym(3)
eq2 = dist(x0, -2r, 0, √Sym(3)a, x, r)- r^2 |> expand |> simplify |> numerator |> factor
eq3 = x0*(√Sym(3)a + r) - r*sqrt(x0^2 + (√Sym(3)a + 2r)^2);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, x, x0) = u
   return [
       sqrt(3)*(3*a^2/4 - sqrt(3)*a*r/2 - 3*a*x/2 - 3*r^2/4 + sqrt(3)*r*x/2 + 3*x^2/4)/3,  # eq1
       -27*a^6*r^2 + 27*a^6*x^2 - 54*a^6*x*x0 + 27*a^6*x0^2 - 108*sqrt(3)*a^5*r^3 + 108*sqrt(3)*a^5*r*x^2 - 162*sqrt(3)*a^5*r*x*x0 + 54*sqrt(3)*a^5*r*x0^2 - 540*a^4*r^4 + 540*a^4*r^2*x^2 - 540*a^4*r^2*x*x0 + 54*a^4*r^2*x0^2 + 18*a^4*x^2*x0^2 - 36*a^4*x*x0^3 + 18*a^4*x0^4 - 480*sqrt(3)*a^3*r^5 + 480*sqrt(3)*a^3*r^3*x^2 - 240*sqrt(3)*a^3*r^3*x*x0 - 96*sqrt(3)*a^3*r^3*x0^2 + 48*sqrt(3)*a^3*r*x^2*x0^2 - 60*sqrt(3)*a^3*r*x*x0^3 + 12*sqrt(3)*a^3*r*x0^4 - 720*a^2*r^6 + 720*a^2*r^4*x^2 - 288*a^2*r^4*x0^2 + 144*a^2*r^2*x^2*x0^2 - 72*a^2*r^2*x*x0^3 - 27*a^2*r^2*x0^4 + 3*a^2*x^2*x0^4 - 6*a^2*x*x0^5 + 3*a^2*x0^6 - 192*sqrt(3)*a*r^7 + 192*sqrt(3)*a*r^5*x^2 + 96*sqrt(3)*a*r^5*x*x0 - 96*sqrt(3)*a*r^5*x0^2 + 64*sqrt(3)*a*r^3*x^2*x0^2 + 16*sqrt(3)*a*r^3*x*x0^3 - 20*sqrt(3)*a*r^3*x0^4 + 4*sqrt(3)*a*r*x^2*x0^4 - 2*sqrt(3)*a*r*x*x0^5 - 2*sqrt(3)*a*r*x0^6 - 64*r^8 + 64*r^6*x^2 + 64*r^6*x*x0 - 32*r^6*x0^2 + 32*r^4*x^2*x0^2 + 32*r^4*x*x0^3 - 4*r^4*x0^4 + 4*r^2*x^2*x0^4 + 4*r^2*x*x0^5,  # eq2
       -r*sqrt(x0^2 + (sqrt(3)*a + 2*r)^2) + x0*(sqrt(3)*a + r),  # eq3
   ]
end;

r = 1/2
iniv = BigFloat[1.7, 0.87, 0.58]
res = nls(H, ini=iniv)

   ([1.7320508075688774, 0.8660254037844387, 0.5773502691896257], true)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (a, x, x0) = [1.7320508075688774, 0.8660254037844387, 0.5773502691896257]
   #@printf("小円の直径が %g のとき，中円の直径は %g である。\n", 2r4, 2r3)
   #@printf("r4 = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", r4, r1, r2, r3, x3, y3)
   plot([a, 0, -a, a], [0, √3a, 0, 0], color=:blue, lw=0.5)
   plot!([x0, 0, -x0, x0], [-2r, √3a, -2r, -2r], color=:green, lw=0.5)
   plot!([0, x, -x, 0], [0, √3x, √3x, 0], color=:blue, lw=1)
   circle2(x, r, r)
   circle(0, -r, r)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x, r, "等円:r,(x,r)", :red, :center, delta=-delta/2)
       point(0, -r, "等円:r,(0,-r)", :red, :center, delta=-delta/2)
       point(a, 0, "a", :blue, :left, :bottom, delta=delta/2)
       point(x0, -2r, " (x0,-2r)", :green, :left, :vcenter)
   end
end;

算額（その1086）

算額（その1086）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円10個，外円，弦

全円の中に水平な弦を引き，その上下に乙円 2 個，丙円 2 個，大円 1 個を入れる。大円の中には甲円 2 個，乙円 2 個が入っている。丙円の直径が 1 寸のとき，全円の直径はいかほどか。

全円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を 2r1, (0 2r1 - R)
甲円の半径と中心座標を r1, (0, r1 - R), (0, 3r1 - R)
乙円の半径と中心座標を r2, (x2, 2r1 - R), (r2, 4r1 - R + r2)
丙円の半径と中心座標を r3, (x3, 4r1 - R - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms R::positive, r1::positive, r2::positive, x2::positive,
     r3::positive, x3::positive, y3::positive,
     r4::positive
eq1 = r2^2 + (4r1 - R + r2)^2 - (R - r2)^2
eq2 = x3^2 + (4r1 - R - r3)^2 - (R - r3)^2
eq3 = x3^2 + (2r1- r3)^2 - (2r1 + r3)^2
eq4 = x2^2 + r1^2 - (r1 + r2)^2
eq5 = x2 + r2 - 2r1
res = solve([eq1, eq2, eq3, eq4, eq5], (R, r1, r2, x2, x3))[1]

   (2401*r3/468, 49*r3/26, 49*r3/39, 98*r3/39, 14*sqrt(13)*r3/13)

全円の半径 R は，丙円の 2401/468 倍である。
丙円の直径が 1 寸のとき，全円の直径は 5 寸と 61/468 である。

divrem(2401, 468)

   (5, 61)

その他のパラメータは以下のとおりである。

  r3 = 0.5;  R = 2.56517;  r1 = 0.942308;  r2 = 0.628205;  x2 = 1.25641;  x3 = 1.94145

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   (R, r1, r2, x2, x3) = (2401*r3/468, 49*r3/26, 49*r3/39, 98*r3/39, 14*sqrt(13)*r3/13)
   @printf("丙円の直径が %g のとき，全円の直径は %g である。\n", 2r3, 2R)
   @printf("r3 = %g;  R = %g;  r1 = %g;  r2 = %g;  x2 = %g;  x3 = %g\n", r3, R, r1, r2, x2, x3)
   plot()
   circle(0, 0, R, :green)
   circle(0, r1 - R, r1)
   circle(0, 3r1 - R, r1)
   circle(0, 2r1 - R, 2r1, :orange)
   circle2(x2, 2r1 - R, r2, :blue)
   circle2(x3, 4r1 - R - r3, r3, :magenta)
   circle2(r2, 4r1 - R + r2, r2, :blue)
   y0 = 4r1 - R
   x0 = sqrt(R^2 - y0^2)
   segment(-x0, y0, x0, y0, :brown)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1 - R, "甲円:r1,(0,r1-R)", :red, :center, delta=-delta/2)
       point(0, 2r1 - R, " 2r1-R", :red, :center, :bottom, delta=delta/2)
       point(0, 4r1 - R, " 4r1-R", :red, :center, delta=-delta/2)
       point(0, 3r1 - R, "甲円:r1,(0,3r1-R)", :red, :center, delta=-delta/2)
       point(x2, 2r1 - R, "乙円:r2\n(x2,2r1-R)", :blue, :center, delta=-delta/2)
       point(r2, 4r1 - R + r2, "乙円:r2\n(r2,4r1-R+r2)", :blue, :center, delta=-delta/2)
       point(x3, 4r1 - R - r3, "丙円:r2\n(x3,4r1-R-r3)", :magenta, :center, :bottom, delta=delta/2)
       point(0, R, "R", :green, :center, :bottom, delta=delta/2)
       point(R, 0, " R", :green, :left, :vcenter)
   end
end;

算額（その1085）

算額（その1085）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円4個，半円1個，四分円2個，正方形

直線の上に大円，小円が載っており，大円の中には水平な元を挟んで，小円 2 個と中円 1 個が入っている。小円の直径が 1 寸のとき，中円の直径はいかほどか。

大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (0, r3), (x3, 2r1 - 3r3), (r1, 2r1 - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     r4::positive
eq1 = r1^2 + r2^2 - (2r1 - r2)^2
eq3 = (2r1 - x3)^2 +y3^2 - (2r1 - r3)^2
eq4 = (x3 - r1)^2 + (2r1 - y3)^2 - (r1 - r3)^2
eq5 = x3^2 + y3^2 - (2r1 + r3)^2
eq2 = 2r2 - r4 - (r1 + r4)
res = solve([eq1, eq2, eq3, eq4, eq5], (r1, r2, r3, x3, y3))[1]

   (4*r4, 3*r4, 4*r4*(26 - sqrt(-52*sqrt(3)*sqrt(19 - 8*sqrt(3)) - 24*sqrt(3) + 733))/13, 4*r4*(2*sqrt(57 - 24*sqrt(3)) + 13)/13, 8*r4*(sqrt(3) + 9)/13)

r3, x3 は二重根号を外して簡約化できる。

res[3] |> sympy.sqrtdenest |> simplify |> println

   4*r4*(-3 + 4*sqrt(3))/13

res[4] |> sympy.sqrtdenest |> simplify |> println

   4*r4*(7 + 8*sqrt(3))/13

中円の半径 r3 は，小円の半径 r4 の 4(4√3 - 3)/13 倍である。
小円の直径が 1 寸のとき，中円の直径は 4(4√3 - 3)/13 = 1.2086779170078488 寸である。

その他のパラメータは以下のとおりである。

   r4 = 0.5;  r1 = 2;  r2 = 1.5;  r3 = 0.604339;  x3 = 3.20868;  y3 = 3.30217

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r4 = 1/2
   (r1, r2, r3, x3, y3) = (4*r4, 3*r4, 4*r4*(26 - sqrt(-52*sqrt(3)*sqrt(19 - 8*sqrt(3)) - 24*sqrt(3) + 733))/13, 4*r4*(2*sqrt(57 - 24*sqrt(3)) + 13)/13, 8*r4*(sqrt(3) + 9)/13)
   @printf("小円の直径が %g のとき，中円の直径は %g である。\n", 2r4, 2r3)
   @printf("r4 = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  y3 = %g\n", r4, r1, r2, r3, x3, y3)
   plot(2r1 .* [0, 1, 1, 0, 0], 2r1 .* [0, 0, 1, 1, 0], color=:green, lw=0.5)
   circle(2r1, 0, 2r1, beginangle=90, endangle=180)
   circle(0, 0, 2r1, beginangle=0, endangle=90)
   circle(r1, 2r1, r1, beginangle=180, endangle=360)
   circle(r1, r2, r2, :blue)
   circle(x3, y3, r3, :magenta)
   circle(2r1 - x3, y3, r3, :magenta)
   circle(r1, 2r2 - r4, r4, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r2, "大円:r2,(r1,r2)", :blue, :center, delta=-delta/2)
       point(x3, y3, "中円:r3,(x3,y3)", :magenta, :center, delta=-delta/2)
       point(r1, 2r2 - r4, "小円:r4\n(r1,2r2-r4)", :green, :center, delta=-delta/2)
       point(r1, 2r1, "(r1,2r1)", :green, :center, :bottom, delta=delta/2)
   end
end;

算額（その1084）

算額（その1084）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：キーワード：円9個，外円，弦

直線の上に大円，小円が載っており，大円の中には水平な元を挟んで，小円 2 個と中円 1 個が入っている。小円の直径が 1 寸のとき，中円の直径はいかほどか。

大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (x2, y2)
小円の半径と中心座標を r3, (0, r3), (x3, 2r1 - 3r3), (r1, 2r1 - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms r1::positive, r2::positive, x2::positive, y2::positive,
     r3::positive, x3::positive
eq1 = r1^2 + (r1 - r3)^2 - (r1 + r3)^2
eq2 = (x3 - x2)^2 + (2r1 - 3r3 - y2)^2 - (r2 + r3)^2
eq3 = (r1 - x2)^2 + (r1 - y2)^2 - (r1 - r2)^2
eq4 = (x3 - r1)^2 + (r1 - 3r3)^2 - (r1 - r3)^2
eq5 = y2 + r2 - (2r1 - 2r3)
res = solve([eq1, eq2, eq3, eq4, eq5], (r1, r2, x2, y2, x3))[4]  # 4 of 4

   (4*r3, r3*(2*sqrt(2) + 3)/2, r3*(sqrt(2) + 2), r3*(9/2 - sqrt(2)), 2*r3*(sqrt(2) + 2))

中円の半径 r2 は，小円の半径 r3 の (2√2 + 3)/2 倍である。
小円の直径が 1 寸のとき，中円の直径は 2.914213562373095 寸である。

その他のパラメータは以下のとおりである。

   r3 = 0.5;  r1 = 2;  r2 = 1.45711;  x2 = 1.70711;  y2 = 1.54289;  x3 = 3.41421

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   (r1, r2, x2, y2, x3) = (4*r3, r3*(2*sqrt(2) + 3)/2, r3*(sqrt(2) + 2), r3*(9/2 - sqrt(2)), 2*r3*(sqrt(2) + 2))
   @printf("小円の直径が %g のとき，中円の直径は %g である。\n", 2r3, 2r2)
   plot()
   circle2(r1, r1, r1, :blue)
   circle2(x2, y2, r2, :green)
   circle2(x3, 2r1 - 3r3, r3)
   circle(0, r3, r3)
   circle2(r1, 2r1 - r3, r3)
   y0 = r1 - 2r3
   x0 = sqrt(r1^2 - y0^2)
   segment(r1 - x0, r1 + y0, r1 + x0, r1 + y0, :magenta)
   segment(x0 - r1, r1 + y0, -r1 - x0, r1 + y0, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r1, "大円:r1,(r1,r1)", :blue, :center, delta=-delta/2)
       point(x2, y2, "中円:r2,(x2, y2)", :green, :center, delta=-delta/2)
       point(0, r3, "小円:r3,(0,r3)", :black, :center, delta=-delta/2)
       point(r1, 2r1 - r3, "小円:r3,(r1,2r1-r3)", :black, :center, delta=-delta/2)
       point(x3, 2r1 - 3r3, "小円:r3,(x4,2r1-3r3)", :black, :center, delta=-delta/2, deltax=-6delta)
       segment(-2r1, 0, 2r1, 0)
   end
end;

算額（その1083）

算額（その1083）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円11個，円弧，1/3円，外円

全円の中に，円弧（1/3円） 2 個，甲円 2 個，乙円 2 個，丙円 4 個，丁円 2 個を容れる。全円の直径が 3 寸のとき，10 個の円（甲，乙，丙，丁）の直径の和はいかほどか。

全円の半径と中心座標を R, (0, 0)
半円の半径と中心座標を R, (0, R), (0, -R)
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (R - r2, 0)
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (x4, 0)

include("julia-source.txt")

using SymPy
@syms R::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     r4::positive, x4::positive
r1 = R/2
x3 = r1 + r3
y3 = r1
eq1 = x3^2 + (R - y3)^2 - (R - r3)^2
eq2 = (R - r2)^2 + R^2 - (R + r2)^2
eq3 = x4^2 + R^2 - (R + r4)^2
eq4 = x4 + r4 + 2r2 - R;
(r2, r3, r4, x4) = solve([eq1, eq2, eq3, eq4], (r2, r3, r4, x4))[1]

   (R/4, R/6, R/12, 5*R/12)

全円の直径　2R が 3 寸のとき，10 個の円（甲，乙，丙，丁）の直径の和は 14R/3 = 7 寸である。

2(2r1 + 2r2 + 4r3 + 2r4) |> println
2(2r1 + 2r2 + 4r3 + 2r4)(R => 3//2) |> println

   14*R/3
   7

その他のパラメータは以下のとおりである。

   R = 1.5;  r1 = 0.75;  r2 = 0.375;  r3 = 0.25;  r4 = 0.125;  x3 = 1;  y3 = 0.75;  x4 = 0.625

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R =3/2
   (r2, r3, r4, x4) = (R/4, R/6, R/12, 5*R/12)
   r1 = R/2
   x3 = r1 + r3
   y3 = r1
   @printf("R = %g;  r1 = %g;  r2 = %g;  r3 = %g;  r4 = %g;  x3 = %g;  y3 = %g;  x4 = %g\n",
       R, r1, r2, r3, r4, x3, y3, x4)
   plot()
   circle(0, 0, R, :blue)
   circle(0, R, R, :blue, beginangle=210, endangle=330)
   circle(0, -R, R, :blue, beginangle=30, endangle=150)
   circle22(0, R - r1, r1, :magenta)
   circle2(R - r2, 0, r2, :red)
   circle4(x3, y3, r3, :green)
   circle2(x4, 0, r4, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
       point(0, R - r1, "甲円:r1,(0,R-r1)", :magenta, :center, delta=-delta/2)
       point(R - r2, 0, "乙円:r2\n(R-r2,0)", :red, :center, delta=-delta/2)
       point(x3, y3, "丙円:r3\n(x3,y3)", :green, :center, delta=-delta/2)
       point(x4, 0, "丁円:r4,(x4,0)", :black, :left, :bottom, delta=delta/2)
   end
end;

算額（その1082）

算額（その1082）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円6個，半円3個，正三角形

正三角形の中に，半円，大円，小円を 3 個ずつ容れる。小円の直径が 1 寸のとき，大円の直径はいかほどか。

半円の半径は正三角形の一辺の長さの √3/2 倍で，その中心は正三角形の辺の中点である。
正三角形の一辺の長さを 2a
半円の半径と中心座標を R, (0, 0), (a/2, √3a/2), (-a/2, √3a/2)
大円の半径と中心座標を r1, (0, R - r1), (x1, r1)
小円の半径と中心座標を r2, (0, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms a::positive, R::positive, r1::positive, x1::positive, r2::positive
R = √Sym(3)a/2
eq1 = x1^2 + r1^2 - (R - r1)^2
eq2 = x1^2 + (R - 2r1)^2 - 4r1^2
eq3 = (a/2)^2 + (√Sym(3)a/2 - r2)^2 - (R + r2)^2
res = solve([eq1, eq2, eq3], (a, r1, x1))[1]

   (8*sqrt(3)*r2, 4*r2, 4*sqrt(3)*r2)

大円の半径は，小円の半径の 4 倍である。
小円の直径が 1 寸のとき，大円の直径は 4 寸である。

その他のパラメータは以下のとおりである。

r2 = 0.5;  a = 6.9282;  r1 = 2;  x1 = 3.4641;  R = 6

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (a, r1, x1) = (8*sqrt(3)*r2, 4*r2, 4*sqrt(3)*r2)
   R = √3a/2
   @printf("r2 = %g;  a = %g;  r1 = %g;  x1 = %g;  R = %g\n",  r2, a, r1, x1, R)
   plot([a, 0, -a, a], [0, √3a, 0, 0], color=:magenta, lw=0.5)
   circle(0, 0, R, :blue,  beginangle=0, endangle=180)
   circle(a/2, √3a/2, R, :blue, beginangle=120, endangle= 300)
   circle(-a/2, √3a/2, R, :blue, beginangle=-120, endangle= 60)
   circle(0, a/√3, r1)
   circle2(x1, r1, r1)
   circle2(0, R + r1, r1)
   circle(0, r2, r2, :green)
   circle((R - r1 - r2)*cosd(30), (R - r1) + (R - r1 - r2)*sind(30), r2, :green)
   circle((R - r1 - r2)*cosd(150), (R - r1) + (R - r1 - r2)*sind(150), r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r1, "大円:r1,(0,R-r1)", :red, :center, delta=-delta/2)
       point(x1, r1, "大円:r1,(x1,r1)", :red, :center, delta=-delta/2)
       point(0, r2, " 小円:r2,(0,r2)", :black, :left, :vcenter)
       point(a/2, √3a/2, "半円:R\n(a/2,√3a/2)", :blue, :left, :vcenter, deltax=2delta)
       point(0, R, " R", :blue, :center, :bottom, delta=delta/2)
       point(0, √3a, " √3a", :blue, :center, :bottom, delta=delta/2)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
       point(a, 0, " a", :magenta, :left, :bottom, delta=delta/2)
   end
end;

算額（その1081）

算額（その1081）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円11個，外円，二等辺三角形（直角三角形）

全円の中に圭（二等辺三角形），甲円 3 個，乙円 1 個，丙円 2 個，丁円 4 個を容れる。丙円の直径が 1 寸のとき，乙円の直径はいかほどか。

注：「問」では圭（二等辺三角形）といっているが底辺は全円の直径である。したがって，三角形は二等辺直角三角形である。

全円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1), (r1, -r1)
乙円の半径と中心座標を r2, (0, r2 - R)
丙円の半径と中心座標を r3, (x3, x3)
丁円の半径と中心座標を r4, (x4, y4), (y4, x4)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy
@syms R::positive, r1::positive, r2::positive, r3::positive, x3::positive
eq1 = 2r1^2 - (R - r1)^2
eq2 = r1^2 + (-r1 -(r2 - R))^2 - (r1 + r2)^2
eq3 = 2x3^2 - (R - r3)^2
eq4 = 2(R - 2r3)^2 - R^2
res = solve([eq1, eq2, eq3, eq4], (r1, r2, x3, R))[2];  # 2 of 2

r1 = res[1] |> sympy.sqrtdenest |> simplify
r2 = res[2] |> sympy.sqrtdenest |> simplify
x3 = res[3] |> sympy.sqrtdenest |> simplify
R = res[4]
(r1, r2, x3, R)

   (2*sqrt(2)*r3, 2*r3*(2 - sqrt(2)), r3*(4 + 3*sqrt(2))/2, 2*r3*(sqrt(2) + 2))

乙円の半径は丙円の半径の 4 - 2√2 = 1.17157287525381 倍である。
丙円の直径が 1 寸のとき，乙円の直径は 1.17157287525381 寸である。

---

これ以降で，図を描くために丁円の半径と中心座標を求める。

パラメータを簡単にするために図を反時計回りに 45° 回転させたものを使う。
まず丁円の半径を求める。算法助術の公式29 を使うまでもなく，以下で求めることができる。中心座標は後で求めるので使わない（使用するためには回転しなければならずかえって面倒になる）。

using SymPy
@syms R::positive, r3::positive, r4::positive, x4::positive, y4::positive
y4 = R - 2r3 + r4
eq5 = x4^2 + y4^2 - (R - r4)^2
eq6 = x4^2 + (r3 - r4)^2 - (r3 + r4)^2
res2 = solve([eq5, eq6], (r4, x4))[1]

   (-r3*(-R + r3)/R, 2*r3*sqrt(R - r3)/sqrt(R))

@syms x4::positive, y4::positive
x3 = r3*(4 + 3√Sym(2))/2
R = 2r3*(√Sym(2) + 2)
r4 = -r3*(-R + r3)/R
eq7 = (x4 - x3)^2 + (y4 - x3)^2 - (r3 + r4)^2 |> expand |> simplify
eq8 = x4^2 + y4^2 - (R - r4)^2 |> expand |> simplify
res3 = solve([eq7, eq8], (x4, y4))[1]

   (-r3*sqrt(47321*sqrt(2) + 66922)/(140 + 99*sqrt(2)) + 5*sqrt(2)*r3/4 + 9*r3/4, r3*sqrt(47321*sqrt(2) + 66922)/(140 + 99*sqrt(2)) + 5*sqrt(2)*r3/4 + 9*r3/4)

丙円の直径が 1 寸のときの描画パラメータは以下のとおりである。

r3= 0.5;  r1 = 1.41421;  r2 = 0.585786;  x3 = 2.06066;  R = 3.41421
r4 = 0.42677669529663687

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   (r1, r2, x3, R) = (2*sqrt(2)*r3, 2*r3*(2 - sqrt(2)), r3*(4 + 3*sqrt(2))/2, 2*r3*(sqrt(2) + 2))
   r4 = -r3*(-R + r3)/R
   (x4, y4) = (-r3*sqrt(47321*sqrt(2) + 66922)/(140 + 99*sqrt(2)) + 5*sqrt(2)*r3/4 + 9*r3/4, r3*sqrt(47321*sqrt(2) + 66922)/(140 + 99*sqrt(2)) + 5*sqrt(2)*r3/4 + 9*r3/4)
   @printf("丙円の直径が %g のとき，乙円の直径は %g である。\n", 2r3, 2r2)
   @printf("r3= %g;  r1 = %g;  r2 = %g;  x3 = %g;  R = %g\n", r3, r1, r2, x3, R)
   plot([0, R, -R, 0], [R, 0, 0, R], color=:hotpink, lw=0.5)
   circle(0, 0, R, :blue)
   circle(0, r1, r1)
   circle2(r1, -r1, r1)
   circle(0, r2 - R, r2, :magenta)
   circle2(x3, x3, r3, :darkred)
   circle2(x4, y4, r4, :green)
   circle2(y4, x4, r4, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :blue, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
       point(0, r1, "甲円:r1,(0,r1)", :red, :center, delta=-delta/2)
       point(r1, -r1, "甲円:r1,(r1,-r1)", :red, :center, delta=-delta/2)
       point(0, r2 - R, "乙円:r2\n(0,r2-R)", :magenta, :center, :bottom, delta=delta/2)
       point(x3, x3, " 丙円:r3,(x3,x3)", :darkred, :center, delta=-delta/2, deltax=-4delta)
       point(x4, y4, " 丁円:r4,(x4,y4)", :green, :center, :bottom, delta=delta, deltax=-4delta)
       point(y4, x4, " 丁円:r4,(y4,x4)", :green, :center, delta=-delta/2, deltax=-8delta)
   end
end;

算額（その1080）

算額（その1080）

九十八 岩手県江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円5個，半円4個，長方形，斜線2本

長方形の中に 2 本の斜線と甲円（半円），乙円，丙円，丁円を容れる。丁円の直径が 1 寸のとき，乙円の直径はいかほどか。

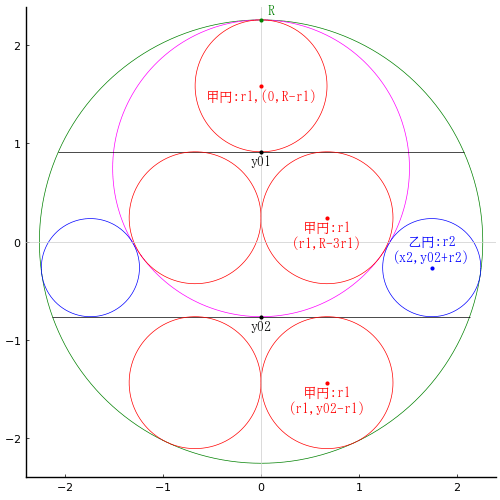
原点を，中央の乙円の中心に置く。」
長方形の短辺，長辺の長さを 2a, 2r2 + 2r1
甲円の半径と中心座標を r1, (r2 + r1)
乙円の半径と中心座標を r2, (a, 0)
丙円の半径と中心座標を r3,（0, r2 + r3)
丁円の半径と中心座標を r4, (x4, y4)
とおき，以下の連立方程式を解く。

eq1, eq2 は他の条件と重複するので除外する。

残念ながら，SymPy で一度に解くことができないので，今回は既知の変数を前もって定義するという対応を取る。

右下がりの斜線と長方形の右辺を下に延長し交点を α とする。右の甲円，乙円の中心 の y 座標を β，γとすると，αβ，αγ を一辺とする直角三角形は相似で，相似比は 1:2 である。したがって，乙円と甲円の半径 r2, r1 は 1:2 である。

また，右下がりの斜線と y 軸の交点の y 座標を δ，中央下の丙円，乙円の中心の y 座標を ε，ζ とすると,δε，δζ を一辺とする直角三角形は相似で，相似比は 1:2 である。したがって，丙円と乙円の半径 r3, r2 は 1:2 である。
これを合わせると，r3:r2:r1 = 4:2:1 なので，r2 = 2r3, r1 = 4r3 という条件を加え，eq5, eq6 は除外する。

これで，もともとは 6 元連立方程式だったものが 4 元連立方程式になった。

include("julia-source.txt")

using SymPy

@syms a::positive, r1::positive, r2::positive,
     r3::positive, x3::positive, y3::positive,
     r4::positive, x4::positive, y4::positive
r2 = 2r3
r1 = 4r3
#eq1 = dist2(0, r1 + r2, a/2, 0, a, 0, r2)
#eq2 = dist2(0, r1 + r2, a/2, 0, 0, 0, r2)
eq3 = dist2(0, r1 + r2, a/2, 0, x4, y4, r4)
eq4 = dist2(0, r1 + r2, a/2, 0, 0, r2 + r3, r3)
#eq5 = dist2(0, r1 + r2, a/2, 0, a, r1 + r2, r1)
eq6 = (a - x4)^2 + (r1 + r2 - y4)^2 - (r1 + r4)^2 |> expand
eq7 = (a - x4)^2 + y4^2 - (r2 + r4)^2 |> expand;
#eq8 = r3/(r1 - r3) - r2/(r1 + r2)
#res = solve([eq3, eq4, eq5, eq6, eq7, eq8], (a, r1, r2, r3, x4, y4))

println(eq3, ",  # eq3")
println(eq4, ",  # eq4")
#println(eq5, ",  # eq5")
println(eq6, ",  # eq6")
println(eq7, ",  # eq7")
#println(eq8, ",  # eq8")

   36*a^2*r3^2 - 12*a^2*r3*y4 - a^2*r4^2 + a^2*y4^2 - 144*a*r3^2*x4 + 24*a*r3*x4*y4 - 144*r3^2*r4^2 + 144*r3^2*x4^2,  # eq3
   8*r3^2*(a^2 - 18*r3^2),  # eq4
   a^2 - 2*a*x4 + 20*r3^2 - 8*r3*r4 - 12*r3*y4 - r4^2 + x4^2 + y4^2,  # eq6
   a^2 - 2*a*x4 - 4*r3^2 - 4*r3*r4 - r4^2 + x4^2 + y4^2,  # eq7

最も式が簡単な eq4 を解いて a を求め，残りの 3 個の方程式に代入することで，更に次元を 1 つ減らすことができる。

ans_a = solve(eq4, a)[1]
ans_a |> println

   3*sqrt(2)*r3

eq3 = eq3(a => ans_a) |> simplify |> (x -> x/18r3^2)
eq6 = eq6(a => ans_a)
eq7 = eq7(a => ans_a) |> simplify
eq3 |> println
eq6 |> println
eq7 |> println

   36*r3^2 - 24*sqrt(2)*r3*x4 - 12*r3*y4 - 9*r4^2 + 8*x4^2 + 4*sqrt(2)*x4*y4 + y4^2
   38*r3^2 - 8*r3*r4 - 6*sqrt(2)*r3*x4 - 12*r3*y4 - r4^2 + x4^2 + y4^2
   14*r3^2 - 4*r3*r4 - 6*sqrt(2)*r3*x4 - r4^2 + x4^2 + y4^2

これで，SymPy でも連立方程式を解くことができるようになる。r3, x4, y4 が，与えられる r4 を含む式で表される。

res = solve([eq3, eq6, eq7], (r3, x4, y4))[1];
res[1] |> simplify |> println
res[2] |> simplify |> println
res[3] |> simplify |> println

乙円の半径 r2 は 丙円の半径 r3 の 2倍，更に r3 は 丁円の半径 r4 の (2√2 + 3)/4 倍である。つまり，r2 = r2*(2√2 + 3)/2 である。
丁円の直径が 1 寸のとき丙円の直径は 2.914213562373095 寸である。

その他のパラメータは以下のとおりである。

r4 = 0.5;  r3 = 0.728553;  x4 = 1.61959;  y4 = 1.29044;  a = 3.09099;  r2 = 1.45711;  r1 = 2.91421

パラメータは以下のようにして逐次求めることができる。

r4 = 0.5
r3 = r4*(2*sqrt(2) + 3)/4
x4 = r4*(12 + 19*sqrt(2))/12
y4 = r4*(7 + 6*sqrt(2))/6
a = 3*sqrt(2)*r3
r2 = 2r3
r1 = 4r3
(a, r1, r2, r3, x4, y4)

   (3.0909902576697323, 2.914213562373095, 1.4571067811865475, 0.7285533905932737, 1.6195857368787003, 1.290440114519881)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r4 = 0.5
   #(a, r1, r2, r3, x4, y4) = res[1]
   r3 = r4*(2*sqrt(2) + 3)/4
   x4 = r4*(12 + 19*sqrt(2))/12
   y4 = r4*(7 + 6*sqrt(2))/6
   a = 3*sqrt(2)*r3
   r2 = 2r3
   r1 = 4r3
   @printf("丁円の直径が %g のとき，乙円の直径は %g である。\n", 2r4, 2r2)
   @printf("r4 = %g;  r3 = %g;  x4 = %g;  y4 = %g;  a = %g;  r2 = %g;  r1 = %g\n",
       r4, r3, x4, y4, a, r2, r1)
   plot([a, a, -a, -a, a], [-r2, r2 + 2r1, r2 + 2r1, -r2, -r2], color=:green, lw=0.5)
   circle(0, 0, r2, :blue)
   circle(a, 0, r2, :blue, beginangle=90, endangle=270)
   circle(-a, 0, r2, :blue, beginangle=-90, endangle=90)
   circle(0, r2 + r3, r3, :magenta)
   circle(0, 2r1 + r2 - r3, r3, :magenta)
   circle(a, r2 + r1, r1, beginangle=90, endangle=270)
   circle(-a, r2 + r1, r1, beginangle=-90, endangle=90)
   circle2(x4, y4, r4, :green)
   x01 = a*(r1 + 2r2)/2(r1 + r2)
   x02 = a*r1/2(r1 + r2)
   segment(a, -r2 - r1, -x02, r2 + 2r1, :orange)
   segment(a, -r2, a, -r2 - r1, :orange)
   segment(-x01, -r2, x02, r2 + 2r1, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, -r2 - r1, " α", :gray50, :left, :vcenter)
       point(a, 0, " β", :gray40, :left, :vcenter)
       point(a, r2 + r1, " γ", :gray40, :left, :vcenter)
       point(0, 0, "ζ ", :gray40, :right, :vcenter, delta=delta)
       point(0, r2 + r3, "ε ", :gray40, :right, :vcenter)
       point(0, r2 + r1, "δ ", :gray40, :right, :vcenter)
       point(a, r2 + r1, "甲円:r1\n(a,r2+r1) ", :red, :right, :vcenter)
       point(a, 0, "乙円:r2 \n(a,0) ", :blue, :right, :vcenter)
       point(0, 0, "乙円:r2,(0,0) ", :blue, :center, delta=-delta/2)
       point(0, r2 + r3, " 丙円:r3,(0,r2+r3) ", :black, :left, :vcenter)
       point(0, 2r1 + r2 - r3, " 丙円:r3,(0,2r1+r2-r3) ", :black, :left, :vcenter)
       point(x4, y4, "丁円:r4,(x4,y4)", :black, :left, delta=-delta/2, deltax=-3delta)
   end
end;

算額（その1079）

算額（その1079）

九十七 岩手県大船渡市猪川町 雨宝堂 現雨宝山竜宝院 文政7年(1824)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード：円9個，外円，弦2本

全円の中に 2 本の水平な弦を引き，大円 1 個，甲円 5 個，乙円 2 個を容れる。乙円の直径が 1 寸のとき，全円の直径はいかほどか。

全円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r0, (0, R - r0)
甲円の半径と中心座標を r1, (0, R - r1), (r1, R - 3r1), (r1, R - 2r0 - r1)
乙円の半径と中心座標を r2, (x2, R - 2r0 + r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r0::positive,
     r1::positive, r2::positive, x2::positive
eq1 = x2^2 + (R - 2r0 + r2)^2 - (R - r2)^2
eq2 = r1^2 + (R - 2r0 - r1)^2 - (R - r1)^2
eq3 = r1^2 + (3r1 - r0)^2 - (r0 - r1)^2
eq4 = x2^2 + (r0 - r2)^2 - (r0 + r2)^2
res = solve([eq1, eq2, eq3, eq4], (R, r1, r0, x2))[1]

   (14641*r2/3240, 121*r2/90, 121*r2/40, 11*sqrt(10)*r2/10)

全円の半径 R は 乙円の半径 r2 の 14641/3240 = 4.518827160493827 倍である。
術では「4 と 1681/3240」と小学校以来使ったことのない帯分数で表している。
したがって，乙円の直径が 1 寸のとき，全円の直径は 14641/3240 = 4.518827160493827 寸である。

その他のパラメータは以下のとおりである。
r2 = 0.672222;  R = 2.25941;  r1 = 0.672222;  r0 = 1.5125;  x2 = 1.73925

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (R, r1, r0, x2) = r2 .* (14641/3240, 121/90, 121/40, 11√10/10)
   @printf("乙円の直径が %g のとき，全円の直径は %g である。\n", 2r2, 2R)
   @printf("r2 = %g;  R = %g;  r1 = %g;  r0 = %g;  x2 = %g\n", r1, R, r1, r0, x2)
   plot()
   circle(0, 0, R, :green)
   circle(0, R - r0, r0, :magenta)
   circle(0, R - r1, r1)
   y01 = R - 2r1
   x01 = sqrt(R^2 - y01^2)
   segment(-x01, y01, x01, y01)
   circle2(r1, R - 3r1, r1)
   y02 = R - 2r0
   x02 = sqrt(R^2 - y02^2)
   segment(-x02, y02, x02, y02)
   circle2(r1, y02 - r1, r1)
   circle2(x2, y02 + r2, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(0, R - r1, "甲円:r1,(0,R-r1)", :red, :center, delta=-delta/2)
       point(r1, R - 3r1, "甲円:r1\n(r1,R-3r1)", :red, :center, delta=-delta/2)
       point(r1, y02 - r1, "甲円:r1\n(r1,y02-r1)", :red, :center, delta=-delta/2)
       point(x2, y02 + r2, "乙円:r2\n(x2,y02+r2)", :blue, :center, :bottom, delta=delta/2)
       point(0, y01, "y01", :black, :center, delta=-delta/2)
       point(0, y02, "y02", :black, :center, delta=-delta/2)
   end
end;