算額（その1078）

算額（その1078）

百 大船渡市猪川町 雨宝堂 現雨宝山竜宝院 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円2個，正三角形，正方形

正方形の中に正三角形 2 個と月円，日円の 2 個の円を容れる。月円の直径が 1 寸のとき，日円の直径はいかほどか。

正方形の一辺の長さを a
正三角形の頂点の座標を (0, b), (b, 0), (a/2, √3a/2)
日円の半径と中心座標を r1, (x1, y1); y1 = x1
月円の半径と中心座標を r2, (r2, y2)
とおき，以下の連立方程式を解く。

日円と月円の方程式は独立なので，別々に解く。

1.　日円について

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive,
     r1::positive, x1::positive, y1::positive,
     r2::positive, y2::positive
b = a*(√Sym(3) - 1)  # a - 2(a - √Sym(3)a/2)
y1 = x1
eq1 = dist2(0, b, a, a, x1, y1, r1)
eq2 = dist2(a/2, √Sym(3)a/2, a, 0, x1, y1, r1)
res1 = solve([eq1, eq2], (r1, x1))[2];
r1 = apart(res1[1]) |> simplify
r1 |> println
x1 = apart(res1[2]) |> simplify
x1 |> println

   a*(-1 + sqrt(3))*sqrt(1 + sqrt(3))*sqrt(-sqrt(2) + sqrt(3))/4
   a*(-sqrt(2) + 2 + sqrt(6))/4

日円の半径は正方形の一辺の長さの (√3 - 1)*sqrt(3 - √6 + √3 - √2)/4 倍である。

2.　月円について

r2 = y2*(2 - √Sym(3))
eq3 = dist2(0, b, b, 0, r2, y2, r2)
y2 = solve(eq3, y2)[2]
y2 = y2 |> sympy.sqrtdenest |> simplify
r2 = y2*(2 - √Sym(3)) |> simplify
r2 |> println
y2 |> println

   a*(-7*sqrt(2) - 5*sqrt(3) + 9 + 4*sqrt(6))/2
   a*(-2*sqrt(2) - sqrt(3) + sqrt(6) + 3)/2

月円の半径は正方形の一辺の長さの (-7√2 - 5√3 + 9 + 4√6)/2 倍である。

3.　月円と日円の比について

月円の直径が 1 のときの日円の直径は r2/r1 = 1.43185165257814 である。

ついでに，月円の直径が 1 寸になるときの正方形の一辺の長さを求めてみる。

@syms d
日円の直径 = apart(r1/r2, d) |> simplify
日円の直径 |> println
日円の直径.evalf() |> println

   -1/2 + sqrt(2)/2 + sqrt(6)/2
   1.43185165257814

正方形（小正三角形）の一辺 の長さは r2 = 1/2 を解いて，a = √2/4 + √6/4 + 3/2 + √3 = 4.197976633857945 である。

eq = r2 - 1//2
res = solve(eq, a)[1]
ans_a = apart(res[1], d)
ans_a |> println
ans_a.evalf() |> println

   sqrt(2)/4 + sqrt(6)/4 + 3/2 + sqrt(3)
   4.19797663385795

4.　図を描いて確認する

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = sqrt(2)/4 + sqrt(6)/4 + 3/2 + sqrt(3)
   b = a*(√3 - 1)
   r1 = a*(√3 - 1)*sqrt(3 - √6 + √3 - √2)/4
   x1 = a*(-√2 + 2 + √6)/4
   r2 = a*(-7√2 - 5√3 + 9 + 4√6)/2
   y2 = a*(-2√2 - √3 + √6 + 3)/2
   @printf("月円の直径が %g のとき，日円の直径は %g である。\n", 2r2, 2r1)
   @printf("a = %g;  r1 = %g;  x1 = %g;  r2 = %g;  y2 = %g\n", a, r1, x1, r2, y2)
   plot([0, a, a, 0, 0], [0, 0, a, a], color=:blue, lw=0.5)
   plot!([0, a, a/2, 0], [0, 0, √3a/2, 0], color=:green, lw=0.5)
   plot!([b, a, 0, b], [0, a, b, 0], color=:magenta, lw=0.5)
   circle(x1, x1, r1)
   circle(r2, y2, r2, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, a, "a ", :blue, :right, :vcenter)
       point(x1, x1, "日円:r1,(x1,x1)", :red, :center, delta=-delta/2)
       point(r2, y2, "月円:r2,(r2,y2)", :orange, :center, delta=-delta/2)
       point(0, b, "b ", :blue, :right, :vcenter)
       point(b, 0, "b", :blue, :center, delta=-delta)
       point(a/2, √3a/2, "(a/2,√3a/2)", :green, :center, :bottom, delta=delta, deltax=-3delta)
       plot!(xlims=(-5delta, a + 5delta), ylims=(-5delta, a + 5delta))
   end
end;

算額（その1077）

算額（その1077）

百 大船渡市猪川町 雨宝堂 現雨宝山竜宝院 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円8個，累円，直線上

直線上に甲円を中心として，左右に乙円，丙円，丁円 が互いに外接している。その上にそれら全ての円に外接する天円が載っている。乙円，丁円の直径がそれぞれ 4 寸，16 寸のとき，天円の直径はいかほどか。

天円の半径と中心座標を R, (0, 2r1 + R)
甲円の半径と中心座標を r1, (0, r1)
乙円の半径と中心座標を r2, (x2, r2)
丙円の半径と中心座標を r3, (x3, r3)
丁円の半径と中心座標を r4, (x4, r4)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive, x1, r2::positive, x2::positive,
     r3::positive, x3::positive, r4::positive, x4::positive
(r2, r4) = (4, 16) .// 2
x1 = 0
eq1 = x2^2 + (2r1 + R - r2)^2 - (R + r2)^2 |> expand
eq2 = x3^2 + (2r1 + R - r3)^2 - (R + r3)^2 |> expand
eq3 = x4^2 + (2r1 + R - r4)^2 - (R + r4)^2 |> expand
eq4 = (x2 - x1)^2 + (r2 - r1)^2 - (r2 + r1)^2 |> expand
eq5 = (x3 - x2)^2 + (r3 - r2)^2 - (r3 + r2)^2 |> expand
eq6 = (x4 - x3)^2 + (r4 - r3)^2 - (r4 + r3)^2 |> expand
eq4 = x2^2 - 4r1*r2
eq5 = (x3 - x2)^2 - 4r2*r3
eq6 = (x4 - x3)^2 - 4r3*r4
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (R, r1, x2, r3, x3, x4))[1]

   (49/4, 7/4, sqrt(14), 28/9, 7*sqrt(14)/3, 5*sqrt(14))

乙円，丁円の直径がそれぞれ 4 寸，16 寸のとき，天円の直径は 49/2 = 24.5 寸である。

「答」では，32 寸としているが，それでは図が描けない。

条件として与えられたのが「乙円径 4 寸，丁円径 16 寸」，答えは「天円径 32 寸」
これを図にしようと，まず直径 32 の天円を描き，それに接するように直径 4 の甲円を描くが，その左に天円に外接する甲円が描けるように天円と乙円の中心座標を調整する。

次に，直径 16 の丁円を天円に外接するように描く。これはたいした苦も無く描ける。次いで，その左に天円と外接するように丙円を描く。これも容易に描ける。
が，しかし。乙円と丙円は外接しない。
要するに，「問」と「答」を満たすような解はないということだ。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r4) = [4, 16] ./ 2
   (R, r1, x2, r3, x3, x4) = (49/4, 7/4, sqrt(14), 28/9, 7*sqrt(14)/3, 5*sqrt(14))
   @printf("乙円，丁円の直径が　%g, %g のとき，天円の直径は %g である。\n", 2r2, 2r4, 2R)
   @printf("(r1 => %.15g, r2 => %.15g, r3 = %.15g, r4 = %.15g)\n", r1, r2, r3, r4)
   plot()
   circle(0, 2r1 + R, R, :blue)
   circle(0, r1, r1)
   circle2(x2, r2, r2, :green)
   circle2(x3, r3, r3, :magenta)
   circle2(x4, r4, r4, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 2r1 + R, "天円:R,(0,2r1+R)", :blue, :center, delta=-delta)
       point(x4, r4, " 丁円:r4,(x4,r4)", :orange, :center, delta=-delta)
       point(x3, r3, " 丙円:r3,(x3,r3)", :magenta, :center, delta=-delta, deltax=10delta)
       point(x2, r2, "乙円:r2,(x2,r2)", :green, :center, delta=10delta)
       point(0, r1, "甲円:r1,(0,r1) ", :black, :right, :vcenter)
   end
end;

インチキな図を書くプログラム

function draw2(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r4) = [4, 16] ./ 2
   (R, r1, x2, r3, x3, x4) = (16, 1.78, 3.73, 3.4, 10.6,20.96)    
   @printf("乙円，丁円の直径が　%g, %g のとき，天円の直径は %g である。\n", 2r2, 2r4, 2R)
   @printf("(r1 => %.15g, r2 => %.15g, r3 = %.15g, r4 = %.15g)\n", r1, r2, r3, r4)
   plot()
   circle(0, 2r1 + R, R, :blue)
   circle(0, r1, r1)
   circle2(x2, r2, r2, :green)
   circle2(x3, r3, r3, :magenta)
   circle2(x4, r4, r4, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 2r1+R, " 天円径=32", :blue, :center, delta=-delta, mark=false)
       point(x4, r4, " 丁円径=16", :orange, :center, delta=-delta, mark=false)
       point(x3, r3, " 丙円", :magenta, :center, :vcenter, mark=false)
       point(x2, r2, "乙円径=4", :green, :center, delta=10delta, mark=false)
       point(0, r1, "甲円", :red, :center, :vcenter, mark=false)
   end
end;

算額（その1076）

算額（その1076）

九十九 江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円9個，円弧4個

交わる 4 個の円弧と甲円 4 個，乙円 5 個がある。乙円の直径が 1 寸のとき，甲円の直径はいかほどか。

円弧を構成する円の半径と中心座標を R, (r2 + R, 0)
甲円の半径と中心座標を r1, (0, r2 + r1)
乙円の半径と中心座標を r2, (0, 0), (x2, y2); y2 = x2
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive, r2::positive, x2::positive, y2::positive
y2 = x2
eq1 = (r2 + R - x2)^2 + y2^2 - (R - r2)^2 |> expand
eq2 = (r2 + R)^2 + (r2 + r1)^2 - (R + r1)^2 |> expand
eq3 = (r2 + R)/2 - x2 |> expand
res = solve([eq1, eq2, eq3], (r1, R, x2))[1]

   (sqrt(2)*r2, r2*(2*sqrt(2) + 3), r2*(sqrt(2) + 2))

甲円の半径 r1 は乙円の半径 r2 の √2 倍である。
乙円の直径が 1 寸のとき，甲円の直径は 1.4142135623730951 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (R, r1, x2) = (r2*(2*sqrt(2) + 3), sqrt(2)*r2, r2*(sqrt(2) + 2))
   @printf("乙円の直径が　%g のとき，甲円の直径は %g である。\n", 2r2, 2r1)
   plot()
   circle(0, 0, r2, :blue)
   circle4(x2, x2, r2, :blue)
   circle42(0, r2 + r1, r1)
   circle42(0, r2 + R, R, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r2 + R, 0, "円弧:R,(r2 + R)", :green, :center, delta=-delta)
       point(r2, 0, " r2", :blue, :left, delta=-delta/2)
       point(r2 + r1, 0, "甲円:r1,(r2+r1,0)", :red, :left, :bottom, delta=delta)
       point(x2, x2, " 乙円:r2,(x2,y2)", :blue, :left, :vcenter)
   end
end;

算額（その1075）

算額（その1075）

九十九 江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円9個，正方形，斜線

正方形の中に 8 本の斜線と大円，中円，小円を容れる。中円と小円の直径の和が 1 寸のとき，大円の直径はいかほどか。

正方形の一辺の長さを 2a
大円の半径と中心座標を r1, (0,0)
中円の半径と中心座標を r2, (cx2, cy2)
小円の半径と中心座標を r3, (cx3, cy3)
とおき，逐次的に解を求める。

1.　大円の半径

最も単純には，大円の中心から斜線までの距離が r1 になるように r1 を求めればよい。
半径は r1 = √5a/5 である。

include("julia-source.txt")

using SymPy

@syms a::positive, r1::positive
eq0 = dist2(0, 0, 2a, a, a, a, r1)
solve(eq0, r1)[1] |> println

   sqrt(5)*a/5

図形を丁寧に描き，計算に必要ないくつかの交点の座標を求めておくと（図参照），大円の直径は線分 AC に等しく，その長さは sqrt((8a/5 - 4a/5)^2 + (4a/5 - 2a/5)^2) = 2√5a/5 である。

sqrt((8a/5 - 4a/5)^2 + (4a/5 - 2a/5)^2) |> println

   2*sqrt(5)*a/5

2.　中円の半径と中心座標

大円と中円は，⊿OAB，⊿OCD に内包されている。⊿OAB と ⊿OCD は相似で，相似比は OA:OC = 2:1 なので，中円の半径は大円の半径の 1/2 で，r2 = r1/2 = √5a/10 である。

@syms r2::positive, cx2::positive, cy2::positive
r1 = √Sym(5)a/5
r2 = r1/2

   sqrt(5)*a/10

中円の中心座標 (cx2, cy2) は，2 本の斜線までの距離が r2 に等しいという連立方程式を解けばよい。

eq1 = dist2(0, 0, a, 2a, cx2, cy2, r2)
eq2 = dist2(0, 0, 2a, a, cx2, cy2, r2)
res1 = solve([eq1, eq2], (cx2, cy2))[1]

   (a/2, a/2)

中円の中心座標は (a/2, a/2) である。

3.　小円の半径と中心座標

中円と小円は，⊿OEF, ⊿HEG に内包されている。⊿OEF, ⊿HEG は相似で，相似比は OF:HG = a:2a/3 = 3:2 なので，小円の半径は中円の半径の 2/3 で，r3 = √5a/15 である。

小円の中心座標 (cx3, cy3) は，中心から線分 GH，GE までの距離が r3 に等しいという連立方程式を解けばよい。

@syms r3::positive, cx3::positive, cy3::positive
r3 = √Sym(5)a/15
eq3 = dist2(0, a, 2a, 2a, cx3, cy3, r3)
eq4 = dist2(0, a, 2a, 0, cx3, cy3, r3)
res2 = solve([eq3, eq4], (cx3, cy3))[1]

   (a/3, a)

小円の中心座標は (a/3, a) である。

4.　小円の半径が与えられたときの大円の半径

これまでをまとめると，小円，中円，大円の半径は √5a/15, √5a/10, √5*a/5 である。

r3, r2, r1

   (sqrt(5)*a/15, sqrt(5)*a/10, sqrt(5)*a/5)

「問」は「中円と小円の直径の和が 1 寸のとき，大円の直径はいかほどか」なので，以下の方程式を解き a を求め，r1 の式に代入すれば大円の半径が求まる。

eq = r2 + r3 - 1//2
solve(eq, a)[1] |> println

   3*sqrt(5)/5

r1(a => 3√Sym(5)/5) |> println

   3/5

大円の半径は 3/5 寸，すなわち，直径は 6/5 = 1.2 寸である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 1
   r1 = sqrt(5)*a/5  # = sqrt((x1 - 2a + y1)^2 + (y1 - x1)^2)/2
   r2 = r1/2
   r3 = 2r2/3
   plot([0, 2a, 2a, 0, 0], [0, 0, 2a, 2a, 0], color=:green, lw=0.5)
   plot!([0, 2a, 0, a, 2a, 0, 2a, a, 0], [0, a, 2a, 0, 2a, a, 0, 2a, 0], color=:blue, lw=0.5)
   circle(a, a, r1, :red, lw=1)
   circle(a/2, a/2, r2, :orange)
   circle(a/3, a, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, "O:(0,0)", :black, :left, delta=-delta/2)
       point(8a/5, 4a/5, " A:(8a/5,4a/5)", :black, :left, delta=-delta/2)
       point(a, 2a, " B:(a,2a)", :black, :center, :bottom, delta=delta/2)
       point(4a/5, 2a/5, " C:(4a/5,2a/5)", :black, :left, delta=-delta/2)
       point(a/2, a, " D:(a/2,a)", :black, :left, :vcenter)
       point(2a/5, 4a/5, "E:(2a/5,4a/5) ", :black, :right, :vcenter)
       point(a, a/2, "  F:(a,a/2)", :black, :left, :vcenter)
       point(0, a, "G:(0,a) ", :black, :right, :vcenter)
       point(2a/3, 4a/3, "H:(2a/3,4a/3) ", :black, :right, :vcenter)
       plot!([a/2, 0, 8a/5, a, a/2, 4a/5], [a, 0, 4a/5, 2a, a, 2a/5], color=:blue, lw=1.5)
       plot!([0, 2a/3,0, a, 0], [0, 4a/3, a, a/2, 0], color=:magenta, lw=1)
       plot!(xlims=(-12delta, 2a + 3delta), ylims=(-5delta, 2a + 3delta))
   end
end;

算額（その1074）

算額（その1074）

九十八 江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円2個，二等辺三角形，正方形，界斜

正方形内に二等辺三角形と甲円，乙円，界斜を容れる。乙円の直径が 1 寸のとき，界斜の長さはいかほどか。

注：算額（山村）の図では，界斜は甲円に接していないように描かれているがそんなことはない。界斜は乙円と甲円の両方に接している。

正方形の一辺の長さを 2a
界斜と正方形の一辺との交点座標を (2a, b)
界斜を延長して x 軸との交点座標を (c, 0)
甲円の半径と中心座標を r1, (a, r1)
乙円の半径と中心座標を r2, (x2, 2a - r2)
とおき，以下の連立方程式を解く。

円の中心から直線までの距離を求める際に，同じ直線でも定義に使う点の座標によって連立方程式が複雑になることがある。この算額でいえば界斜を (0, 2a) - (2a, b) で定義するのと (0, 2a) - (c, 0) で定義する場合に当たる。連立方程式が少しでも複雑になると SymPy で解けなくなってしまうので，工夫が必要になる。

図において ⊿ABX と ⊿OCX は相似で，界斜の長さは BC*2a/C になる。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, c::positive,
     r1::positive, r2::positive, x2::positive
#eq1 = dist2(0, 2a, 2a, b, a, r1, r1)
#eq2 = dist2(0, 2a, 2a, b, x2, 2a - r2, r2)
eq1 = dist2(0, 2a, c, 0, a, r1, r1)/4a
eq2 = dist2(0, 2a, c, 0, x2, 2a - r2, r2)/4a
eq3 = dist2(0, 0, a, 2a, a, r1, r1)
eq4 = dist2(0, 0, a, 2a, x2, 2a - r2, r2)
eq5 = r1*x2 - r2*(c - a)
res = solve([eq2, eq3, eq4, eq5], (a, r1, x2, c))[2];

@syms d
res[1] |> factor |> println
apart(res[2]) |> factor |>  println
apart(res[3]) |> factor |> println
res[4] |> factor |> println

   r2*(-sqrt(10*sqrt(5) + 23) + 5 + 3*sqrt(5) + sqrt(5)*sqrt(10*sqrt(5) + 23))/4
   -r2*(-3*sqrt(10*sqrt(5) + 23) - 5 - sqrt(5) + sqrt(5)*sqrt(10*sqrt(5) + 23))/4
   r2*(-sqrt(10*sqrt(5) + 23) + sqrt(5) + 3 + sqrt(5)*sqrt(10*sqrt(5) + 23))/4
   r2*(7 + 4*sqrt(5) + sqrt(5)*sqrt(10*sqrt(5) + 23))/2

以上をまとめて，a, r1, x2, c は以下のようにして求めることができる。

r2 = 1/2
t = sqrt(10√5 + 23)
a = r2*(5 - t + √5(3 + t))/4
r1 = r2*(5 + 3t + √5(1 - t))/4
x2 = r2*(3 - t + √5(1 + t))/4
c = r2*(7 + √5(4 + t))/2
(r2, a, r1, x2, c)

   r2 = 0.5;  a = 2.50415;  r1 = 1.54765;  x2 = 1.69513;  c = 7.75107

乙円の直径が 1 寸のとき，界斜の長さは sqrt(4a^2 +c^2)*(2a/c) = 5.962810866213448 寸である。

sqrt(4a^2 +c^2)*(2a/c)

   5.962810866213448

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 0.5
   t = sqrt(10√5 + 23)
   a = r2*(5 - t + √5(3 + t))/4
   r1 = r2*(5 + 3t + √5(1 - t))/4
   x2 = r2*(3 - t + √5(1 + t))/4
   c = r2*(7 + √5(4 + t))/2
   len = sqrt(4a^2 + c^2)*2a/c
   @printf("乙円の直径が %g のとき，界斜は %g である。\n", 2r2, len)
   @printf("r2 = %g;  a = %g;  r1 = %g;  x2 = %g;  c = %g\n", r2, a, r1, x2, c)
   plot([0, 2a, 2a, 0, 0], [0, 0, 2a, 2a, 0], color=:green, lw=0.5)
   plot!([0, a, 2a], [0, 2a, 0], color=:blue, lw=0.5)
   circle(a, r1, r1)
   circle(x2, 2a - r2, r2, :magenta)
   segment(0, 2a, c, 0)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(2a, 0, " 2a", :black, :left, :bottom, delta=delta/2, deltax=-0.5delta)
       point(2a, 2a*(c - 2a)/c, " (2a,b)", :black, :left, :vcenter)
       point(c, 0, " C", :red, :left, :bottom, delta=delta/2)
       point(a, 2a, " A", :red, :left, :bottom, delta=delta/2)
       point(0, 2a, "B ", :red, :right, :bottom, delta=delta/2)
       point(0, 0, "O ", :red, :right, :bottom, delta=delta/2)
       (x0, y0) = intersection(0, 2a, c, 0, 0, 0, a, 2a)
       point(float(x0), float(y0), "  X", :red, :left, :vcenter)
       plot!(xlims=(-5delta, c + delta))
   end
end;

算額（その1073）

算額（その1073）

九十八 江刺市 雨宝堂 現中善観音堂 文政10年(1827)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円13個，外円

外円の中に，甲円 2 個，乙円 4 個，丙円 2 個，丁円 4 個を容れる。丁円の直径が 1 寸のとき，丙円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0); R - 2r1
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (x2, r2)
丙円の半径と中心座標を r3, (x3, 0)
丁円の半径と中心座標を r4, (x4, y4)
とおき，以下の連立方程式を解く。

一度に解けない。しかし，丙円は最終的には丁円との関連を問われるが，甲円，乙円，丁円は丙円とは独立に決めることができるので，まず eq1, eq2, eq3, eq5, eq7 の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive,
     r2::positive, x2::positive,
     r3::positive, x3::positive,
     r4::positive, x4::positive, y4::positive
R = 2r1
eq1 = x2^2 + r2^2 - (R -r2)^2 |> expand
eq2 = x4^2 + y4^2 - (R - r4)^2 |> expand
eq3 = x2^2 + r2^2 - (r1 + r2)^2 |> expand
eq4 = x3^2 + (R - r1)^2 - (r1 + r3)^2 |> expand
eq5 = x4^2 + (y4 - R + r1)^2 - (r1 + r4)^2 |> expand
eq6 = (x2 - x3)^2 + r2^2 - (r2 + r3)^2 |> expand
eq7 = (x2 - x4)^2 + (y4 - r2)^2 - (r2 + r4)^2 |> expand;
res = solve([eq1, eq2, eq3, eq5, eq7], (r1, r2, x2, x4, y4))[1]

   (sqrt(2)*r4 + 5*r4/2, sqrt(2)*r4/2 + 5*r4/4, 2*r4 + 5*sqrt(2)*r4/2, 2*r4*sqrt(2*sqrt(2) + 3), 2*r4*(1 + sqrt(2)))

x4 は二重根号を外すことができる。

res[1] |> simplify |> println
res[2] |> simplify |> println
res[3] |> simplify |> println
res[4] |> sympy.sqrtdenest |> println
res[5] |> simplify |> println

   r4*(2*sqrt(2) + 5)/2
   r4*(2*sqrt(2) + 5)/4
   r4*(4 + 5*sqrt(2))/2
   2*r4*(1 + sqrt(2))
   2*r4*(1 + sqrt(2))

r1, r2, x2, x4, y4 が決まったので，残りの r3, x3 を求める。

r1 = √Sym(2)r4 + 5r4/2
r2 = √Sym(2)r4/2 + 5r4/4
x2 = 2r4 + 5√Sym(2)r4/2
x4 = 2r4*(1 + √Sym(2))
y4 = 2r4 + 2√Sym(2)r4
R = 2r1
eq4 = x3^2 + (R - r1)^2 - (r1 + r3)^2 |> expand
eq6 = (x2 - x3)^2 + r2^2 - (r2 + r3)^2 |> expand
res2 = solve([eq4, eq6], (r3, x3))[1]

   (-5*r4 - 2*sqrt(2)*r4 + 2*sqrt(2)*(8*r4/7 + 10*sqrt(2)*r4/7), 8*r4/7 + 10*sqrt(2)*r4/7)

r3 は更に簡約化できる。

res2[1] |> simplify |> println
res2[2] |> simplify |> println

   r4*(2*sqrt(2) + 5)/7
   2*r4*(4 + 5*sqrt(2))/7

丙円の半径 r3 は，丁円の半径 r4 の (2√2 + 5)/7 倍である。
丁円の直径が 1 寸のとき，丙円の直径は (2√2 + 5)/7 = 1.1183467321065985 寸である。

(2√2 + 5)/7

   1.1183467321065985

その他のパラメータは以下のとおりである

   r4 = 0.5;  r1 = 1.95711;  r2 = 0.978553;  x2 = 2.76777;  x4 = 2.41421;  y4 = 2.41421;  r3 = 0.559173;  x3 = 1.58158;  R = 3.91421

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r4 = 1/2
   r1 = √2r4 + 5r4/2
   r2 = √2r4/2 + 5r4/4
   x2 = r4*(2 + 5√2/2)
   x4 = 2r4*(1 + √2)
   y4 = 2r4*(1 + √2)
   r3 = r4*(2√2 + 5)/7
   x3 = 2r4*(4 + 5√2)/7
   R = 2r1
   @printf("丁円の直径が %g のとき，丙円の直径は %g である。\n", 2r4, 2r3)
   @printf("r4 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  x4 = %g;  y4 = %g;  r3 = %g;  x3 = %g;  R = %g\n",
       r4, r1, r2, x2, x4, y4, r3, x3, R)
   plot()
   circle(0, 0, R, :orange)
   circle22(0, R - r1, r1)
   circle4(x2, r2, r2, :blue)
   circle2(x3, 0, r3, :magenta)
   circle4(x4, y4, r4, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r1, "甲円:r1,(0,R-r1)", :red, :center, delta=-delta/2)
       point(x2, r2, "乙円:r2,(x2,r2)", :blue, :center, delta=-delta/2)
       point(x3, 0, "丙円:r3,(x3,0)", :magenta, :left, delta=-delta/2, deltax=-4delta)
       point(x4, y4, "丁円:r4,(x4,y4)", :green, :left, delta=-delta/2, deltax=-4delta)
       point(R, 0, " R", :black, :left, :bottom, delta=delta/2, deltax=-0.5delta)
   end
end;

算額（その1072）

算額（その1072）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

正方形の中に楕円，元円，利円，貞円，享円を容れる。貞円の直径が 1 寸のとき，元円の直径はいかほどか。

注1：利円，享円の条件については何も述べられていない。実際，制限はあるもののどんな値も取りうる。
注2：算額の図（山村の図）では，楕円が楕円らしくないが，それはよくあることかもしれないが，結果に影響を与えるかもしれない。

正方形の一辺の長さを 2a
楕円の長半径，短半径，中心座標を a, b, (0, b); b = a - r1
元円の半径と中心座標を r1, (0, 2a - r1), (r1, a), (r1, a - 2r1)
貞円の半径と中心座標を r2, (a - r3, r3)
楕円と元円の接点座標を (x1, y1)
楕円と貞円の接点座標を (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive,
     r1::positive, x1::positive, y1::positive,
     r2::positive, x2::positive, y2::positive
b = a - r1
eq1 = x2^2/a^2 + (y2 - a + r1)^2/b^2 - 1
eq2 = (x2 - a + r2)^2 + (y2 - r2)^2 - r2^2
eq3 = -b^2*x2/(a^2*(y2 - a + r1)) - (a - r2 - x2)/(y2 - r2)
eq4 = x1^2/a^2 + (y1 - a + r1)^2/b^2 - 1
eq5 = (x1 - r1)^2 + (y1 - a)^2 - r1^2
eq6 = -b^2*x1/(a^2*(y1 - a + r1)) - (r1 - x1)/(y1 - a);

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, r1, x1, y1, x2, y2) = u
   return [
       -1 + (-a + r1 + y2)^2/(a - r1)^2 + x2^2/a^2,  # eq1
       -r2^2 + (-r2 + y2)^2 + (-a + r2 + x2)^2,  # eq2
       -(a - r2 - x2)/(-r2 + y2) - x2*(a - r1)^2/(a^2*(-a + r1 + y2)),  # eq3
       -1 + (-a + r1 + y1)^2/(a - r1)^2 + x1^2/a^2,  # eq4
       -r1^2 + (-a + y1)^2 + (-r1 + x1)^2,  # eq5
       -(r1 - x1)/(-a + y1) - x1*(a - r1)^2/(a^2*(-a + r1 + y1)),  # eq6
   ]
end;

r2 = 1/2
iniv = BigFloat[2.1, 0.63, 0.83, 2.6, 1.5, 0.52]
res = nls(H, ini=iniv)

   ([3.5742972321311055, 1.1362300699229417, 1.470601088978576, 4.6602138004791485, 2.755899335723288, 0.8855162507120506], true)

元円の直径は 2*1.1362300699229417 = 2.2724601398458835 である。「答」では 2.243 寸有奇となっており，かなり異なった結論になった。

ちなみに，楕円の長半径，短半径は 3.5743, b = 2.43807 とこれまた，あまりきれいな数ではない。

2*1.1362300699229417

   2.2724601398458835

その他のパラメータは以下のとおりである。

   r2 = 0.5;  a = 3.5743;  b = 2.43807;  r1 = 1.13623;  r2 = 0.5;  x1 = 1.4706;  y1 = 4.66021;  x2 = 2.7559;  y2 = 0.885516

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (a, r1, x1, y1, x2, y2) = res[1]
   b = a - r1
   @printf("貞円の直径が %g のとき，元円の直径は %g である。\n", 2r2, 2r1)
   @printf("r2 = %g;  a = %g;  b = %g;  r1 = %g;  r2 = %g;  x1 = %g;  y1 = %g;  x2 = %g;  y2 = %g\n",
       r2, a, b, r1, r2, x1, y1, x2, y2)
   plot([a, a, -a, -a, a], [0, 2a, 2a, 0, 0], color=:green, lw=0.5)
   ellipse(0, a - r1, a, b, color=:blue)
   circle(0, 2a - r1, r1)
   circle2(r1, a, r1)
   circle2(r1, a - 2r1, r1)
   circle2(a - r2, r2, r2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x2,  y2, "(x2,y2) ", :green, :right, :bottom, delta=2delta, deltax=4delta)
       point(x1,  y1, "(x1,y1)", :green, :left, :bottom, delta=delta/2)
       point(r1, a, "元円:r1,(r1, a)", :red, :center, delta=-delta/2)
       point(r1, a - 2r1, "元円:r1,(r1, a-2r1)", :red, :center, :bottom, delta=delta/2)
       point(0, 2a - r1, "元円:r1,(0,2a-r1)", :red, :center, delta=-delta/2)
       point(a - r2, r2, "貞円:r3,(a-r3,r3)", :green, :center, delta=-delta/2)
       point(0, 2a - 2r1, "2a-2r1", :blue, :center, delta=-delta/2)
       point(0, a - r1, "a-r1", :blue, :center, delta=-delta/2)
   end
end;

算額（その1071）

算額（その1071）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

全円の中に甲円と心円，および乙円から始まる累円（丙円，丁円，戊円，己円...）が入っている。甲円の直径は全円の半径に等しい。心円の直径が 8 寸 9 分のとき，己円の直径を求めよ。

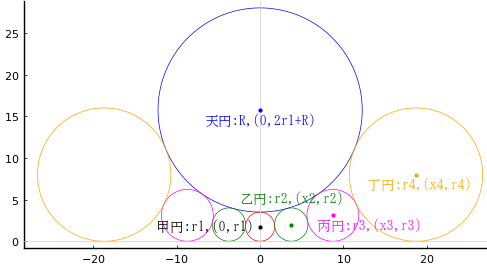
全円の半径と中心座標を R, (0, 0); R = 2r1
甲円の半径と中心座標を r1, (0, r1)
心円の半径と中心座標を r2, (0, -r2)
乙円の半径と中心座標を r3, (x3, y3); x3 = r3，y3 < 0
丙円の半径と中心座標を r4, (x4, y4)
とおく。

まず，甲円の半径 r1 と乙円のパラメータ r3, x3, y3 を求める。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive,
     r3::positive, y3::negative,
     r2::positive
R = 2r1
eq1 = r3^2 + (r1 - y3)^2 - (r1 + r3)^2
eq2 = r3^2 + (r2 + y3)^2 - (r3 + r2)^2
eq3 = r3^2 + y3^2 - (R - r3)^2
res = solve([eq1, eq2, eq3], (r1, r3, y3))[1]

   (7*r2, 56*r2/9, -14*r2/3)

累円は，「ある円に外接する，半径が小さい次の円」の連続である。
乙円と丙円の関係は全円と甲円 の半径により，以下の連立方程式で得られる漸化式で計算される。

@syms R::positive, r1::positive,
     r3::positive, y3::negative,
     r2::positive
R = 2r1
@syms r4, x4, y4, x3
#x3 = r3
#(r1, r2, y3) =  (7*r2, 56*r2/9, -14*r2/3)
eq4 = x4^2 + (r1 - y4)^2 - (r1 + r4)^2
eq5 = x4^2 + y4^2 - (R - r4)^2
eq6 = (x4 - x3)^2 + (y4 - y3)^2 - (r3 + r4)^2
res = solve([eq4, eq5, eq6], (r4, x4, y4))[1]

   ((8*r1^3 + 4*r1^2*r3 - 20*r1^2*y3 - 2*r1*r3^2 - 4*r1*r3*y3 + 10*r1*x3^2 + 14*r1*y3^2 - r3^3 + 3*r3^2*y3 + r3*x3^2 + r3*y3^2 - 3*x3^2*y3 - 2*sqrt(2)*x3*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4) - 3*y3^3)/(2*(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2)), (8*r1^2*x3 - 4*r1*r3*x3 - 4*r1*x3*y3 + 2*sqrt(2)*r1*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4) - 4*r3^2*x3 + sqrt(2)*r3*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4) + 4*x3^3 + 4*x3*y3^2 - 3*sqrt(2)*y3*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4))/(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2), 3*sqrt(2)*x3*sqrt(-(-4*r1^2 - 4*r1*r3 - r3^2 + x3^2 + y3^2)*(2*r1*r3 - 2*r1*y3 - r3^2 + x3^2 + y3^2))/(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2) + (-8*r1^3 + 4*r1^2*r3 + 12*r1^2*y3 + 10*r1*r3^2 - 12*r1*r3*y3 + 2*r1*x3^2 - 6*r1*y3^2 + 3*r3^3 - 9*r3^2*y3 - 3*r3*x3^2 - 3*r3*y3^2 + 9*x3^2*y3 + 9*y3^3)/(2*(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2)))

これにより得られる式は，丙円と丁円，丁円と己円...にも同じように適用される。以下の関数は，ある円 r3, x3, y3 の次の円の 半径，中心の x, y 座標を返す。
これを次々に適用することにより，累円のパラメータを求めることができる。

nextcircle(r1, r3, x3, y3) = ((8*r1^3 + 4*r1^2*r3 - 20*r1^2*y3 - 2*r1*r3^2 - 4*r1*r3*y3 + 10*r1*x3^2 + 14*r1*y3^2 - r3^3 + 3*r3^2*y3 + r3*x3^2 + r3*y3^2 - 3*x3^2*y3 - 2*sqrt(2)*x3*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4) - 3*y3^3)/(2*(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2)), (8*r1^2*x3 - 4*r1*r3*x3 - 4*r1*x3*y3 + 2*sqrt(2)*r1*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4) - 4*r3^2*x3 + sqrt(2)*r3*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4) + 4*x3^3 + 4*x3*y3^2 - 3*sqrt(2)*y3*sqrt(8*r1^3*r3 - 8*r1^3*y3 + 4*r1^2*r3^2 - 8*r1^2*r3*y3 + 4*r1^2*x3^2 + 4*r1^2*y3^2 - 2*r1*r3^3 - 2*r1*r3^2*y3 + 2*r1*r3*x3^2 + 2*r1*r3*y3^2 + 2*r1*x3^2*y3 + 2*r1*y3^3 - r3^4 + 2*r3^2*x3^2 + 2*r3^2*y3^2 - x3^4 - 2*x3^2*y3^2 - y3^4))/(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2), 3*sqrt(2)*x3*sqrt(-(-4*r1^2 - 4*r1*r3 - r3^2 + x3^2 + y3^2)*(2*r1*r3 - 2*r1*y3 - r3^2 + x3^2 + y3^2))/(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2) + (-8*r1^3 + 4*r1^2*r3 + 12*r1^2*y3 + 10*r1*r3^2 - 12*r1*r3*y3 + 2*r1*x3^2 - 6*r1*y3^2 + 3*r3^3 - 9*r3^2*y3 - 3*r3*x3^2 - 3*r3*y3^2 + 9*x3^2*y3 + 9*y3^3)/(2*(4*r1^2 + 4*r1*r3 - 12*r1*y3 + r3^2 - 6*r3*y3 + 8*x3^2 + 9*y3^2)));

甲円の初期パラメータ (r3, x3, y3) = (27.68888888888889, 27.68888888888889, -20.76666666666667) をはじめとして，累円のパラメータを実際に求めてみる。

nextcircle(31.15, 14.658823529411768, 43.976470588235316, 18.3235294117647)

   (7.55151515151515, 37.75757575757576, 39.645454545454534)

nextcircle(31.15, 7.55151515151515, 37.75757575757576, 39.645454545454534)

   (4.371929824561412, 30.603508771929828, 49.18421052631578)

プログラムで書いてみると以下のようになる。

r2 = 8.9/2
(r1, r3, y3) = (7*r2, 56*r2/9, -14*r2/3)
R = 2r1
(r, x, y) = (r3, r3, y3)
for i = 1:10
   println((r, x, y))
   (r, x, y) = nextcircle(31.15, r, x, y)
end

   (27.68888888888889, 27.68888888888889, -20.76666666666667)
   (14.658823529411762, 43.976470588235294, 18.32352941176471)
   (7.551515151515154, 37.75757575757576, 39.64545454545455)
   (4.371929824561407, 30.60350877192981, 49.18421052631579)
   (2.7999999999999976, 25.199999999999978, 53.899999999999984)
   (1.931782945736425, 21.24961240310076, 56.5046511627907)
   (1.4079096045197808, 18.302824858757038, 58.07627118644067)
   (1.0695278969957025, 16.042918454935606, 59.09141630901287)
   (0.8390572390572382, 14.263973063973097, 59.782828282828284)
   (0.6753387533875355, 12.83143631436317, 60.2739837398374)

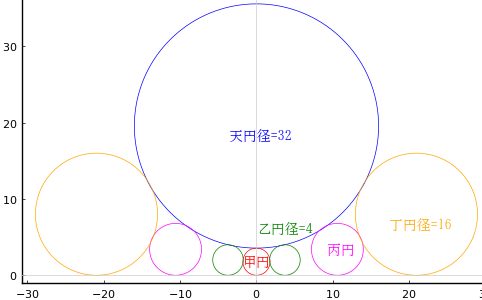
己円の半径は 2.7999999999999976 である（直径は 5.6 寸）。

なお，累円の半径は分数で表すことができ，分子は 1246 で，分母は g(n) = 20n^2 - 20n + 45 である。

using Printf
g(n) = 20n^2 - 20n + 45;
for n = 1:10
   @printf("n = %2d,  分母 = %4d,  半径 = %.15g\n", n, g(n), 1246/g(n))
end

   n =  1,  分母 =   45,  半径 = 27.6888888888889
   n =  2,  分母 =   85,  半径 = 14.6588235294118
   n =  3,  分母 =  165,  半径 = 7.55151515151515
   n =  4,  分母 =  285,  半径 = 4.3719298245614
   n =  5,  分母 =  445,  半径 = 2.8
   n =  6,  分母 =  645,  半径 = 1.93178294573643
   n =  7,  分母 =  885,  半径 = 1.40790960451977
   n =  8,  分母 = 1165,  半径 = 1.06952789699571
   n =  9,  分母 = 1485,  半径 = 0.839057239057239
   n = 10,  分母 = 1845,  半径 = 0.675338753387534

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   names = Char["甲乙丙丁戊己庚辛壬癸"...]
   r2 = 8.9/2
   (r1, r3, y3) = (7*r2, 56*r2/9, -14*r2/3)
   R = 2r1
   @printf("心円の直径が %g のとき，己円の直径は %g である。\n", 2r2, 2r3)
   plot(showaxis=false)
   delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
   circlef(0, 0, R, :orange)
   circlef(0, r1, r1, :green)
   circlef(0, -r2, r2, :purple)
   (rnow, xnow, ynow) = (r3, r3, y3)
   for i = 1:9
       @printf("%s: R = %.15g;  r1 = %.15g;  r = %.15g;  x = %.15g;  y = %.15g\n", names[i+1], R, r1, rnow, xnow, ynow)
       circlef(xnow, ynow, rnow, i)
       circlef(-xnow, ynow, rnow, i)
       point(xnow, ynow, names[i+1], :white, :center, :vcenter, mark=false)
       (rnow, xnow, ynow) = nextcircle(31.15, rnow, xnow, ynow)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       #hline!([0], color=:gray80, lw=0.5)
       #vline!([0], color=:gray80, lw=0.5)
       point(0, r1, "甲", :white, :center, :vcenter, mark=false)
       point(0, -r2, "心", :white, :center, :vcenter, mark=false)
   end
end;

   心円の直径が 8.9 のとき，己円の直径は 55.3778 である。
   乙: R = 62.3;  r1 = 31.15;  r = 27.6888888888889;  x = 27.6888888888889;  y = -20.7666666666667
   丙: R = 62.3;  r1 = 31.15;  r = 14.6588235294118;  x = 43.9764705882353;  y = 18.3235294117647
   丁: R = 62.3;  r1 = 31.15;  r = 7.55151515151515;  x = 37.7575757575758;  y = 39.6454545454545
   戊: R = 62.3;  r1 = 31.15;  r = 4.37192982456141;  x = 30.6035087719298;  y = 49.1842105263158
   己: R = 62.3;  r1 = 31.15;  r = 2.8;  x = 25.2;  y = 53.9
   庚: R = 62.3;  r1 = 31.15;  r = 1.93178294573643;  x = 21.2496124031008;  y = 56.5046511627907
   辛: R = 62.3;  r1 = 31.15;  r = 1.40790960451978;  x = 18.302824858757;  y = 58.0762711864407
   壬: R = 62.3;  r1 = 31.15;  r = 1.0695278969957;  x = 16.0429184549356;  y = 59.0914163090129
   癸: R = 62.3;  r1 = 31.15;  r = 0.839057239057238;  x = 14.2639730639731;  y = 59.7828282828283

デカルトの円定理を用いる方法

円の直径（半径）だけを求めるならば，デカルトの円定理を使って，累円の半径を求めてゆくことができる。
半径 r1, prev, nxt の 3 円が内接する外円の半径を R とすると，以下の式が成り立つ。

using SymPy
@syms R, r1, prev, nxt
nxtr = -1/(1/r1 + 1/prev + 1/nxt - 2sqrt(1/(r1*prev) + 1/(prev*nxt) + 1/(nxt*r1))) - R

これを解いて nxt を求める式を得る。

result = solve(nxtr, nxt)[1]
result |> println

   (R*prev*r1*(R*prev + R*r1 - prev*r1) - 2*sqrt(-R^3*prev^3*r1^3*(-R + prev + r1)))/(R^2*prev^2 - 2*R^2*prev*r1 + R^2*r1^2 + 2*R*prev^2*r1 + 2*R*prev*r1^2 + prev^2*r1^2)

これを関数にする。この関数は，円の半径を入力すれば，その円に外接する次の円の半径を返す。

res2(prev, R, r1) = (R*prev*r1*(R*prev + R*r1 - prev*r1) - 2*sqrt(-R^3*prev^3*r1^3*(-R + prev + r1)))/(R^2*prev^2 - 2*R^2*prev*r1 + R^2*r1^2 + 2*R*prev^2*r1 + 2*R*prev*r1^2 + prev^2*r1^2)

   res2 (generic function with 1 method)

R, r1, r3 が求まった段階で，次々に関数を適用してゆく。

r2 = 8.9/2
r1 = 7*r2
R = 2r1
r3 = r2 * 56/9  # 乙円
(r2, R, r1, r3)

   (4.45, 62.300000000000004, 31.150000000000002, 27.68888888888889)

nxt = res2(r3, R, r1)  # 丙円

   14.65882352941177

nxt = res2(nxt, R, r1)  # 丁円

   7.551515151515152

nxt = res2(nxt, R, r1)  # 戊円

   4.371929824561404

nxt = res2(nxt, R, r1)  # 己円

   2.8000000000000003

nxt = res2(nxt, R, r1)    # 庚円

   1.9317829457364344

 

算額（その1070）

算額（その1070）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

正方形の中に直角三角形と，甲円，乙円，丙円，丁円を容れる。正方形の一辺の長さが 2 寸のとき，4 個の円の和はいかほどか。正方形の一辺の長さは弦（直角三角形の斜辺）の 4/5 である。

最後の一文は，条件なのかヒントなのか?

正方形の一辺の和を a
正方形の辺上にある正三角形の頂点座標を (b, a), (0, c)
直角三角形の 3 辺の長さを ab, bc, ca
甲円の半径と中心座標を r1, (a - r1, a - r1)
乙円の半径と中心座標を r2, (r2, r2)
丙円の半径と中心座標を r3, (x3, y3)
丁円の半径と中心座標を r4, (r4, a - r4)
とおき，以下の連立方程式を解く。

11 元連立方程式であるが，eq1〜eq9 までの条件式は簡単なものなので，SymPy でも簡単に 9 元連立方程式の解（b, c, ab, bc, ca, r1, r2, r3, r4）を求めることができる。
残るパラメータ (x3, y3) は eq10, eq11 の連立方程式を解けばよい。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, c::positive,
     ab::positive, bc::positive, ca::positive,
     r1::positive, r2::positive, r3::positive, r4::positive,
     x3::positive, y3::positive;
eq1 = bc^2 + ca^2 - ab^2
eq2 = (a - b) + a - ab - 2r1
eq3 = c + a - ca - 2r2
eq4 = bc + ca - ab - 2r3
eq5 = b + (a - c) - bc - 2r4
eq6 = ((a - b) + a + ab)*r1 + (c + a + ca)*r2 + ( bc + ca + ab)*r3 + (b + (a - c) + bc)*r4 - 2a^2
eq6 = 4ab/5 - a
eq7 = (a - b)^2 + a^2 - ab^2
eq8 = c^2 + a^2 - ca^2
eq9 = b^2 + (a - c)^2 - bc^2
eq10 = dist2(a, 0, 0, c, x3, y3, r3)
eq11 = dist2(a, 0, b, a, x3, y3, r3)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8, eq9], (b, c, ab, bc, ca, r1, r2, r3, r4))[1]

   (a/4, a/2, 5*a/4, sqrt(5)*a/4, sqrt(5)*a/2, a/4, a*(3 - sqrt(5))/4, a*(-5 + sqrt(5))/8 + sqrt(5)*a/4, a*(3/8 - sqrt(5)/8))

4 円の直径の和は 2(r1 + r2 + r3 + r4) = 3a/2 である。a = 2 寸のとき 4 円の和は 3 寸である。

2(res[6] + res[7] + res[8] + res[9]) |> simplify |> println

   3*a/2

算額の解答はここまで。

以下は，図を描くために丙円の中心座標 (x3, y3) を求める。
b, c, r3 がわかると，x3, y3 もわかる。

b = a/4
c = a/2
r3 = a*(-5 + sqrt(Sym(5)))/8 + sqrt(Sym(5))*a/4
eq10 = dist(a, 0, 0, c, x3, y3) - r3^2
eq11 = dist(a, 0, b, a, x3, y3) - r3^2
(x3, y3) = solve([eq10, eq11], (x3, y3))[2];

x3, y3 は短く簡約化できる。

@syms d
apart(x3) |> println

   a*(9/8 - 3*sqrt(5)/8)

y3 |> simplify |> sympy.sqrtdenest |> println

   a*(7 - sqrt(5))/8

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 2
   (b, c, ab, bc, ca, r1, r2, r3, r4) = a .* (1/4, 1/2, 5/4, √5/4, √5/2, 1/4, (3 - √5)/4, (√5 - 5)/8 + √5/4, (3 - √5)/8)
   (x3, y3) = a .* ((9 - 3√5)/8, (7 - √5)/8)
   plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:green, lw=0.5)
   plot!([0, a, b, 0], [c, 0, a, c], color=:blue, lw=0.5)
   circle(a - r1, a - r1, r1)
   circle(r2, r2, r2, :green)
   circle(x3, y3, r3, :magenta)
   circle(r4, a - r4, r4, :purple)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :green, :left, :bottom, delta=delta/2)
       point(b, a, " (b,a)", :green, :center, :bottom, delta=delta/2)
       point(0, c, "c ", :green, :right, :vcenter)
       point(a - r1, a - r1, "甲円:r1,(a-r1,a-r1)", :red, :center, delta=-delta/2)
       point(r2, r2, "乙円:r2,(r2,r2)", :green, :center, delta=-delta/2)
       point(x3, y3, "丙円:r3,(x3,y3)", :magenta, :center, delta=-delta/2)
       point(r4, a - r4, "丁円:r4\n(r4,a-r4)", :purple, :center, :bottom, delta=delta/2)
       plot!(xlims=(-4delta, a + 3delta))
   end
end;

算額（その1069）

算額（その1069）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

交差する2個の乙円の隙間に，甲円 3 個，乙円 4 個を容れる。丙円の直径が 5 寸のとき，乙円の直径はいかほどか。

甲円の半径と中心座標を r1, (0, 0), (0, 2r1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (0, 2r1), (0, -2r1); r3 = 2r1
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms r1::positive, r2::positive, x2::positive, y2::positive, r3::positive;
r1 = r3/2
eq1 = x2^2 + (r1 + y2)^2 - (r3 + r2)^2
eq2 = x2^2 + (2r1 - y2)^2 - (r1 + r2)^2
eq3 = x2^2 + (y2 - r1)^2 - (r3 - r2)^2
res = solve([eq1, eq2, eq3], (r2, x2, y2))[1]

   (3*r3/10, 2*sqrt(3)*r3/5, 3*r3/5)

乙円の半径 r2 は，丙円の半径 r3 の 3/10 倍である。
丙円の直径が 5 寸のとき，乙円の直径は 1.5 寸である。

「答」，「術」共に（山村も）「丙円径五寸」なのに，「乙円径九寸」と書いている。数値自体もおかしいが，図を見ても，乙円が丙円より大きいことはありえないことがわかるだろうに。

その他のパラメータは以下のとおりである。

   r3 = 2.5;  r1 = 1.25;  r2 = 0.75;  x2 = 1.73205;  y2 = 1.5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 5/2
   r1 = r3/2
   (r2, x2, y2) = (3*r3/10, 2*sqrt(3)*r3/5, 3*r3/5)
   @printf("丙円の直径が %g のとき，乙円の直径は %g である。\n", 2r3, 2r2)
   @printf("その他のパラメータは以下のとおりである。\n")
   @printf("r3 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  y2 = %g\n", r3, r1, r2, x2, y2)
   plot()
   circle22(0, r1, r3)
   circle4(x2, y2, r2, :green)
   circle22(0, 2r1, r1, :blue)
   circle(0, 0, r1, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 2r1, "甲円:r1,(0,2r1)", :blue, :center, :bottom, delta=delta)
       point(x2, y2, "乙円:r2\n(x2,y2)", :green, :center, :bottom, delta=delta)
       point(0, r1, "丙円:r3\n(0,r1)", :red, :center, :bottom, delta=delta)
   end
end;

算額（その1068）

算額（その1068）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

全円の中に，交差する 2 個の甲円，6 個の等円を容れる。等円の直径が 1 寸のとき，全円の直径はいかほどか。

全円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1)
等円の半径と中心座標を r2, (r2, 0), (x2, r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, r1::positive, r2::positive, x2::positive;
eq1 = x2^2 + r2^2 - (R - r2)^2
eq2 = x2^2 + (R - r1 - r2)^2 - (r1 + r2)^2
eq3 = r2^2 + (R - r1)^2 - (r1 - r2)^2
res = solve([eq1, eq2, eq3], (R, r1, x2))[1]

   (r2*(sqrt(5) + 3), r2*(1 + sqrt(5)), 2*r2*sqrt(2 + sqrt(5)))

全円の半径 R は，等円の半径 r2 の √5 + 3 倍である。
等円の直径が 1 のとき，全円の直径は 5.23606797749979 である。

その他のパラメータは以下のとおりである。
   r2 = 0.5;  R = 2.61803;  r1 = 1.61803;  x2 = 2.05817

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (R, r1, x2)= r2 .* (√5 + 3, √5 + 1, 2sqrt(√5 + 2))
   @printf("等円の直径が %g のとき，全円の直径は %g である。\n", 2r2, 2R)
   @printf("その他のパラメータは以下のとおりである。\nr2 = %g;  R = %g;  r1 = %g;  x2 = %g\n", r2, R, r1, x2)
   plot()
   circle(0, 0, R)
   circle22(0, R - r1, r1, :green)
   circle4(x2, r2, r2, :blue)
   circle2(r2, 0, r2, :blue)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :red, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(0, R - r1, "甲円:r1,(0,R-r1)", :green, :center, delta=-delta/2)
       point(r2, 0, "等円:r2\n(r2,0)", :blue, :center, delta=-delta/2)
       point(x2, r2, "等円:r2\n(x2,r2)", :blue, :center, delta=-delta/2)
   end
end;

算額（その1067）

算額（その1067）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

等脚台形の中に，直径 1 寸の等円 6 個を容れる。大頭（下底），小頭（上底）はいかほどか。

大頭，小頭を 2a, 2b，高さを h とする。
等円の半径と中心座標を r, (r, h - r), (0, 3r), (0, r), (2r, r)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, h::positive, r::positive;
eq1 = dist2(a, 0, b, h, 2r, r, r)
eq2 = r*h - (a - b)*(h - 2r)
eq3 = r^2 + (h - r - 3r)^2 - 4r^2
res = solve([eq1, eq2, eq3], (a, b, h))[2]  # 2 of 3

   (r*(-sqrt(3) + 2*sqrt(2 - sqrt(3)) + 4), r*(-1 + sqrt(3)) + 2*r*sqrt(2 - sqrt(3)), r*(sqrt(3) + 4))

大頭 2a, 小頭 2b, 高さ h は等円の直径の (2sqrt(2 - √3) - √3 + 4) 倍, (√3 - 1 + 2sqrt(2 - √3)) 倍, (√3 + 4)/2 倍である。
等円の直径 = 1 のとき，大頭 = 3.303225372841206，小頭 = 1.7673269879789604，高さ = 2.8660254037844384 寸である。

(2sqrt(2 - √3) - √3 + 4), (√3 - 1 + 2sqrt(2 - √3), (√3 + 4)/2)

   (3.303225372841206, (1.7673269879789604, 2.8660254037844384))

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (a, b, h) = r .* (2sqrt(2 - √3) - √3 + 4, √3 - 1 + 2sqrt(2 - √3), (√3 + 4))
   @printf("等円の直径 = %g のとき，大頭 = %g，小頭 = %g，高さ = %g\n", 2r, 2a, 2b, h)
   plot([a, b, -b, -a, a], [0, h, h, 0, 0], color=:blue, lw=0.5)
   circle2(r, h -r, r, :red)
   circle(0, 3r, r, :red)
   circle(0, r, r, :red)
   circle2(2r, r, r, :red)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(b, h, "(b,h)", :blue, :left, :bottom, delta=delta/2)
       point(a, 0, "a", :blue, :left, :bottom, delta=delta/2)
       point(r, h - r, "(r,h-r)", :red, :center, delta=-delta/2)
       point(0, 3r, " 3r", :red, :left, :vcenter)
       point(0, r, " r", :red, :left, :vcenter)
       point(2r, r, "(2r,r)", :red, :center, delta=-delta/2)
   end
end;

算額（その1066）

算額（その1066）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

大円内に正三角形 4 個，中円 1 個と小円 4 個を入れる。小円の直径がわかっているとき中円の直径を求めるすべを求めよ。

算額（その841）の中央の正方形内に円を内接させただけのものである。条件式は同じなので，何を未知数にして解くかにすぎない。

大円の半径と中心座標を R, (0, 0)
正三角形の一辺の長さを 2a
とおき，以下の方程式を解く。

include("julia-source.txt")

using SymPy

@syms R::positive, a::positive, r::positive;
R = (1 + sqrt(Sym(3)))a
eq1 = dist(R, 0, a, a, (R - r)/sqrt(Sym(2)), (R - r)/sqrt(Sym(2))) - r^2
res = solve(eq1, a)[2];

@syms d
res = res/r |> simplify |> (x -> apart(x, d)) |> factor |> (x -> x*r);
res |> println

   -r*(-10 - 3*sqrt(6) + 3*sqrt(2) + 4*sqrt(3))/4

小円の直径が 1 のとき，中円の直径は 1.54440632773869 である。

res(r => 1).evalf() |> println

   1.54440632773869

小円の直径が 1 のとき，大円の直径は 4.219396554912972 である。

R = (1 + √3) * 1.54440632773869
R |> println

   4.219396554912972

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   a = r*(10 + 3√6 - 3√2 - 4√3)/4
   R = (1 + √3)a
   @printf("小円の直径 = %g;  大円の直径 = %g;  中円の直径 = %g\n", 2r, 2R, 2a)
   plot([a, a, -a, -a, a], [ -a, a, a, -a, -a], color=:blue, lw=0.5)
   circle(0, 0, R, :green)
   # R2 = (4√6 - 1)/4
   # circle(0, 0, R2, :black)
   circle4((R - r)/√2, (R - r)/√2, r)
   circle(0, 0, a, :orange)
   for i in 0:3
       deg = 90i
       plot!([√2a*cosd(deg + 45), R*cosd(deg), √2a*cosd(deg - 45)],
             [√2a*sind(deg + 45), R*sind(deg), √2a*sind(deg - 45)], color=:magenta, lw=0.5)
   end
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, a, "(a,a) ", :blue, :right, delta=-delta/2)
       point(0, (1 + √3)a, " R=(1+√3)a", :green, :center, :bottom, delta=delta/2)
       point((R - r)/√2, (R - r)/√2, "((R-r)/√2,\n(R-r)/√2)", :red, :center, :bottom, delta=delta/2)
   end
end;

算額（その1065）

算額（その1065）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

正方形の中に，四分円，半円，甲乙丙丁戊円を容れる。甲乙丙丁戊の 7 個の円の直径の和が 1 寸のとき，正方形の一辺の長さはいかほどか。

正方形の一辺の長さを 2a
甲円の半径と中心座標を r1, (2a - r1, r1)
乙円の半径と中心座標を r2, (x2, y2)
丙円の半径と中心座標を r3, (x3, 2a - x3)
丁円の半径と中心座標を r4, (x4, 2a - x4)
戊円の半径と中心座標を r5, (r5, y5)
とおき，以下の連立方程式を解く。

図形は複雑そうに見えるが，それぞれの円を決定する条件は互いに独立なので，一つずつ決定していけばよい。

1.　甲円を確定する

include("julia-source.txt");

using SymPy
@syms d1::positive, d2::positive, d3::positive, d4::positive, d5::positive
@syms a::positive, r1::positive
eq1 = (2a - r1)^2 + (a - r1)^2 - (a + r1)^2
r1 = solve(eq1, r1)[1]
r1 |> println

   2*a*(2 - sqrt(3))

2.　乙円を確定する

@syms r2::positive, x2::positive, y2::positive
eq2 = (2a - x2)^2 + y2^2 - (2a - r2)^2
eq3 = x2^2 + (a - y2)^2 - (a - r2)^2
eq4 = (a - x2)^2 + (2a - y2)^2 - (a + r2)^2
(r2, x2, y2) = solve([eq2, eq3, eq4], (r2, x2, y2))[1]
(r2, x2, y2) |> println

   (2*a*(-1 + 3*sqrt(2))/17, 2*a*(6 - sqrt(2))/17, 2*a*(13/17 - 5*sqrt(2)/17))

3.　丙円を確定する

@syms r3::positive, x3::positive
eq5 = x3^2 + (a - x3)^2 - (a - r3)^2
eq6 = 2(2a - x3)^2 - (2a + r3)^2
(r3, x3) = solve([eq5, eq6], (r3, x3))[1]
(r3, x3) |> println

   (-a*(4/3 - 2*sqrt(2)/3) + 2*a/3, a*(4/3 - 2*sqrt(2)/3))

4.　丁円を確定する

@syms r4::positive, x4::positive
eq7 = x4^2 + (a - x4)^2 - (a - r4)^2
eq8 = 2(2a - x4)^2 - (2a - r4)^2
(r4, x4) = solve([eq7, eq8], (r4, x4))[1]
(r4, x4) |> println

   (-2*a + 6*a*(4/7 - sqrt(2)/7), 2*a*(4/7 - sqrt(2)/7))

5.　戊円を確定する

@syms r5::positive, y5::positive
eq9 = (a - r5)^2 + (2a - y5)^2 - (a + r5)^2
eq10 = (2a - r5)^2 + y5^2 - (2a + r5)^2
(r5, y5) = solve([eq9, eq10], (r5, y5))[1]
(r5, y5) |> println

   (-a + 2*a*(2 - sqrt(2)), 2*a*(2 - sqrt(2)))

6.　正方形の一辺の長さを求める

全ての円の直径の和が 1 寸という条件は以下のようになる。

eq = 2(r1 + 2r2 + r3 + r4 + 2r5) - 1 |> simplify;
eq |> println

   -2488*sqrt(2)*a/357 - 4*sqrt(3)*a + 7516*a/357 - 1

この方程式を解いて a を求め，2 倍したものが正方形の一辺の長さである。

a = solve(eq, a)[1]
a |> println
2a.evalf() |> println

   -357/(-7516 + 1428*sqrt(3) + 2488*sqrt(2))
   0.468483001717576

正方形の一辺の長さは 0.468483001717576 寸である。

7.　図を描く

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = -357/(-7516 + 1428*sqrt(3) + 2488*sqrt(2))
   r1 = 2a*(2 - √3)
   plot([0, 2a, 2a, 0, 0], [0, 0, 2a, 2a, 0], color=:black, lw=0.5)
   circle(2a, 0, 2a, beginangle=90, endangle=180)
   circle(0, a, a, :blue, beginangle=-90, endangle=90)
   circle(a, 2a, a, :blue, beginangle=180, endangle=360)
   circle(2a - r1, r1, r1, :green)
   (r2, x2, y2) = (2*a*(-1 + 3*sqrt(2))/17, 2*a*(6 - sqrt(2))/17, 2*a*(13/17 - 5*sqrt(2)/17))
   circle(x2, y2, r2, :magenta)
   circle(2a - y2, 2a - x2, r2, :magenta)
   (r3, x3) = (-a*(4/3 - 2*sqrt(2)/3) + 2*a/3, a*(4/3 - 2*sqrt(2)/3))
   circle(x3, 2a - x3, r3, :orange)
   (r4, x4) = (-2*a + 6*a*(4/7 - sqrt(2)/7), 2*a*(4/7 - sqrt(2)/7))
   circle(x4, 2a - x4, r4, :tomato)
   (r5, y5) = (-a + 2*a*(2 - sqrt(2)), 2*a*(2 - sqrt(2)))
   circle(r5, y5, r5, :purple)
   circle(2a - y5, 2a - r5, r5, :purple)
   @printf("正方形の一辺の長さは %g 寸である。\n", 2a)
   @printf("その他のパラメータは以下のとおりである。\nr1 = %g;  r2 = %g;  x2 = %g;  y2 = %g;  r3 = %g;  x3 = %g;  r4 = %g;  x4 = %g;  r5 = %g;  y5 = %g\n", r1, r2, x2, y2, r3, x3, r4, x4, r5, y5)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 2a, "2a", :black, :left, :bottom, delta=delta/2)
       point(2a - r1, r1, "甲円:r1,(2a-r1,r1)", :green, :center, delta=-delta/2)
       point(x2, y2, "乙円:r2,(x2,y2)", :magenta, :center, delta=-delta/2)
       point(x3, 2a - x3, "丙円:r3\n(x3,2a-x3)", :orange, :center, delta=-delta/2)
       point(x4, 2a - x4, "丁円:r4\n(x4,2a-x4)", :tomato, :center, delta=-delta/2)
       point(r5, y5, "戊円:r5\n(r5,y5)", :purple, :center, delta=-delta/2)
   end
end;

算額（その1064）

算額（その1064）

九十六 大船渡市立根 気仙安養寺稲荷堂 文政5年(1822)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

大円の中に，中円 1 個，小円 5 個を容れる。小円の直径が 1 寸のとき，大円の直径はいかほどか。なお，中円の直径は大円の半径に等しい。

大円の半径と中心座標を R, (0, 0); R = 2r1
中円の半径と中心座標を r1, (0, r1 - R)
小円の半径と中心座標を r2, (0, R - r2), (x21, y21), (x22, y22)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     x21::positive, y21::positive,
     x22::positive, y22::negative
R = 2r1
eq1 = x21^2 + y21^2 - (R - r2)^2 |> expand
eq2 = x22^2 + y22^2 - (R - r2)^2 |> expand
eq3 = x22^2 + (y22 - r1 + R)^2 - (r1 + r2)^2 |> expand
eq4 = x21^2 + (R - r2 - y21)^2 - 4r2^2 |> expand
eq5 = (x22 - x21)^2 + (y21 - y22)^2 - 4r2^2 |> expand;

一度に解くことができないので，まずeq2, eq3, eq4, eq5 から x21, y21, x22, y22 を求める。

res = solve([eq2, eq3, eq4, eq5], (x21, y21, x22, y22))[2];
#= x22 =#  res[3] |> println
#= y22 =#  res[4] |> println

   2*sqrt(2)*sqrt(r2)*sqrt(r1 - r2)
   -2*r1 + 3*r2

式が簡単になる x22, y22 のみを採用し，連立方程式を組み直す（eq2, eq3 は意味を持たなくなるので除外）。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive,
     x21::positive, y21::positive,
     x22::positive, y22::negative
R = 2r1
x22 = 2*sqrt(Sym(2))*sqrt(r2)*sqrt(r1 - r2)
y22 = -2*r1 + 3*r2
eq1 = x21^2 + y21^2 - (R - r2)^2 |> expand
eq4 = x21^2 + (R - r2 - y21)^2 - 4r2^2 |> expand
eq5 = (x22 - x21)^2 + (y21 - y22)^2 - 4r2^2 |> expand;

println(eq1, ",  # eq1")
println(eq4, ",  # eq4")
println(eq5, ",  # eq5")

   -4*r1^2 + 4*r1*r2 - r2^2 + x21^2 + y21^2,  # eq1
   4*r1^2 - 4*r1*r2 - 4*r1*y21 - 3*r2^2 + 2*r2*y21 + x21^2 + y21^2,  # eq4
   4*r1^2 - 4*r1*r2 + 4*r1*y21 - 4*sqrt(2)*sqrt(r2)*x21*sqrt(r1 - r2) - 3*r2^2 - 6*r2*y21 + x21^2 + y21^2,  # eq5

eq1, eq4, eq5 から，r1, x21, x22 を求める。

res2 = solve([eq1, eq4, eq5], (r1, x21, y21))[1]

   (r2*(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0) + 2 + sqrt(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0)^2 + 8))/4, r2*sqrt(-2*CRootOf(x^3 - 2*x^2 + 2*x - 2, 0)^2 + 8 + 2*sqrt(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0)^2 + 8)*CRootOf(x^3 - 2*x^2 + 2*x - 2, 0))/2, r2*CRootOf(x^3 - 2*x^2 + 2*x - 2, 0))

(CRootOf(x^3 - 2*x^2 + 2*x - 2, 0) は x^3 - 2*x^2 + 2*x - 2 = 0 の実数解を得る関数である。具体的には 1.54368901269208 という数値である。

@syms x
term = sympy.CRootOf(x^3 - 2*x^2 + 2*x - 2, 0).evalf() |> println

   1.54368901269208

eq = x^3 - 2x^2 + 2x - 2
solve(eq)[3].evalf() |> println

   1.54368901269208

r2 が与えられたとき，以上をまとめて，r1, R, x21, y21, x22, y22 を求める手順を示す。

r2 = 1/2
term = 1.54368901269208
r1 = r2*(term + 2 + sqrt(term^2 + 8))/4
R = 2r1
x21 = r2*sqrt(-2*term^2 + 8 + 2*sqrt(term^2 + 8)*term)/2
y21 = r2*term
x22 = 2sqrt(2r2*(r1 - r2))
y22 = 3r2 - 2r1
(R, r1, x21, y21, x22, y22)

   (1.69148788395312, 0.84574394197656, 0.9076890632978463, 0.77184450634604, 1.175999901320676, -0.19148788395312)

中円の半径は，小円の半径の (term + 2 + sqrt(term^2 + 8))/4 = 1.69148788395312 倍，
大円の半径は，中円の半径の 2 倍である。
したがって，大円の半径は 小円の半径の 3.38297576790624 倍である。
小円の直径が 1 寸のとき，大円の直径は 3.38297576790624 寸である。

(term + 2 + sqrt(term^2 + 8))/4

   1.69148788395312

「術」も相当複雑なことをやっている。
結局数値解を求めることになってしまったので，最初から数値解を求めればよかった。

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r1, x21, y21, x22, y22) = u
   return [
       -4*r1^2 + 4*r1*r2 - r2^2 + x21^2 + y21^2,  # eq1
       -4*r1^2 + 4*r1*r2 - r2^2 + x22^2 + y22^2,  # eq2
       -2*r1*r2 + 2*r1*y22 - r2^2 + x22^2 + y22^2,  # eq3
       4*r1^2 - 4*r1*r2 - 4*r1*y21 - 3*r2^2 + 2*r2*y21 + x21^2 + y21^2,  # eq4
       -4*r2^2 + x21^2 - 2*x21*x22 + x22^2 + y21^2 - 2*y21*y22 + y22^2,  # eq5
   ]
end;

r2 = 1/2
iniv = BigFloat[10, 10, 15, 13, 2] ./ 10
res = nls(H, ini=iniv)

   ([0.8457439419765593, 0.907689063297846, 0.7718445063460382, 1.175999901320675, -0.19148788395311875], true)

小円の直径が 1 のとき，大円の直径は 3.38298 である。

その他のパラメータは以下のとおりである。

   r2 = 0.5;  r1 = 0.845744;  R = 1.69149;  x21 = 0.907689;  y21 = 0.771845;  x22 = 1.176;  y22 = -0.191488

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   term = 1.54368901269208
   r1 = r2*(term + 2 + sqrt(term^2 + 8))/4
   R = 2r1
   x21 = r2*sqrt(-2*term^2 + 8 + 2*sqrt(term^2 + 8)*term)/2
   y21 = r2*term
   x22 = 2sqrt(2r2*(r1 - r2))
   y22 = 3r2 - 2r1
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r2, 2R)
   @printf("その他のパラメータは以下のとおりである。\nr2 = %g;  r1 = %g;  R = %g;  x21 = %g;  y21 = %g;  x22 = %g;  y22 = %g\n", r2, r1, R, x21, y21, x22, y22)
   plot()
   circle(0, 0, R)
   circle(0, R - r2, r2, :blue)
   circle2(x21, y21, r2, :blue)
   circle2(x22, y22, r2, :blue)
   circle(0, r1 - R, r1, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(0, r1 - R, "大円:r2,(0,r1-R)", :green, :center, delta=-delta/2)
       point(0, R - r2, "小円:r2,(0,R-r2)", :blue, :center, delta=-delta/2)
       point(x21, y21, "小円:r2,(x21,y21)", :blue, :center, delta=-delta/2)
       point(x22, y22, "小円:r2,(x22,y22)", :blue, :center, delta=-delta/2)
   end
end;