平均律vs純正律シリーズ 純正律の調律を体験しよう / Structure of Perfect Intonation Tun
平均律vs純正律シリーズ 各調律法による和音聴き比べ(C-Dur基準版)
平均律vs純正律シリーズ 純正律の調律を体験しよう / Structure of Perfect Intonation Tun
平均律vs純正律シリーズ 各調律法による和音聴き比べ(C-Dur基準版)
http://ja.wikipedia.org/wiki/%E4%B8%AD%E5%85%A8%E9%9F%B3%E5%BE%8Bから
中全音律(ちゅうぜんおんりつ)(英: meantone temperament)は、西洋音楽の代表的な音律の一つである。ミーントーンと呼ばれることも多い。15~19世紀に主に鍵盤楽器の調律で広く使用された。
三度音程の純正度を確保するために、完全五度音程を純正音程よりも僅かに狭めた音律であり、全音の音程は大全音(9/8)と小全音(10/9)の間の大きさとなるために中全音律と呼ばれる。狭義には純正な長三度が得られる1/4コンマ中全音律を指す。
1/4コンマ中全音律(en:Quarter-comma meantone)は、ピタゴラス音律の純正な完全五度を1/4シントニックコンマ狭くすることで、純正な長三度を得るものである。
十七度の音程は、例えばD4からF6#のような音程であり、以下のように表現できる。
あるいは
したがって十七度をピタゴラス音律の純正な完全五度 (3/2) を4つ積み重ねたものとして表すと

一方、純正な長三度 (5/4) と2つのオクターヴ (2/1) を用いて表すと
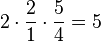
これはピタゴラス音律の長三度が純正音程よりも81/80だけ広いことを意味している。この差をシントニックコンマと呼び、約21.506セントである。
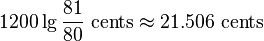
完全五度を純正音程から1/4シントニックコンマ狭めることで、4つの完全五度の積み重ねが純正な十七度 (5/1) と一致し、純正な長三度が得られる。
xを狭められた完全五度とすると、4つの完全五度の積み重ねが5/1になるので

したがって完全五度は
![x = sqrt[4]{5} = 5^{1/4}](http://upload.wikimedia.org/math/a/7/1/a710e5b4cf8242b7bf67aab8e2fbdead.png)
この1/4コンマ中全音律の完全五度は約696.578セントである
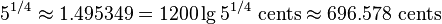
これは純正な完全五度よりも少しだけ狭い。

両者の差は1/4シントニックコンマである。

半音階の12の音は、ある音を起点に完全五度ずつ上昇、下降を繰り返すことによって得られる。これは完全五度の大きさが少し異なること以外はピタゴラス音律と同様である。
以下の表にD音を起点とした1/4コンマ中全音律の半音階の各音の、Dからの音程の大きさを周波数比とセント値で記す。計算式の![x = sqrt[4]{5} = 5^{1/4}](http://upload.wikimedia.org/math/a/7/1/a710e5b4cf8242b7bf67aab8e2fbdead.png) は調整され狭められた完全五度である。
は調整され狭められた完全五度である。
| 音名 | Dからの音程 | 計算式 | 比率 | 大きさ (セント) |
|---|---|---|---|---|
| A♭ | 減五度 |  |
1.4311 | 620.5 |
| E♭ | 短二度 |  |
1.0700 | 117.1 |
| B♭ | 短六度 |  |
1.6000 | 813.7 |
| F | 短三度 |  |
1.1963 | 310.3 |
| C | 短七度 | 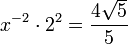 |
1.7889 | 1006.8 |
| G | 完全四度 | 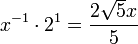 |
1.3375 | 503.4 |
| D | 一度 |  |
1.0000 | 0.0 |
| A | 完全五度 |  |
1.4953 | 696.6 |
| E | 長二度 |  |
1.1180 | 193.2 |
| B | 長六度 | 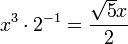 |
1.6719 | 889.7 |
| F♯ | 長三度 |  |
1.2500 | 386.3 |
| C♯ | 長七度 |  |
1.8692 | 1082.9 |
| G♯ | 増四度 |  |
1.3975 | 579.5 |
ピタゴラス音律と同様に、この方法で得られるA♭とG#は一致しない。12音の音階を構成する場合、一般にA♭が省かれる(もちろん取捨選択は自由である)。このときG♯からE♭への五度音程は、他の調整された完全五度とは逆に、純正な完全五度よりも大分広いものになる。この広い五度による和音は、顕著なうなりを生じるため、狼の吠声に例えてウルフの五度(en:Wolf interval)と呼ばれる。また、ウルフの五度を含んだ4つの五度を重ねて出来た十七度に基づく長三度も同様に外れた音程となる。これらの音程は一般には実用に耐えないため、使用できる調は限定されたものとなる。1/4コンマ中全音律では一般的に調号が#が3つあるいは♭が2つより多い調は演奏不可能とされる。
中全音律では異名同音的音程は異なる大きさを持つ。表に上記の12の音からの各音程のおおよそのセント値を示す。
その定義上、1/4コンマ中全音律の11の完全五度は、純正な完全五度より1/4シントニックコンマ分狭い、約696.6セントである。五度圏を閉じるためには、平均律がそうであるように、12の完全五度の平均値は700セントであることが要求されるため、 残る1つは約737.6セントになる(ウルフの五度)。このウルフの五度は異名同音による五度であるため、より正確には減六度である。
以上のように、中全音律では異名同音的音程の大小関係がピタゴラス音律とは逆転している。
ジョゼッフォ・ツァルリーノはLe istitutioni harmoniche (1558) で、シントニックコンマを7分割し、完全五度を2/7コンマ狭めた、2/7コンマ中全音律を記述している。これは長短三度が共に純正音程よりも1/7コンマ狭くなる。
フランシスコ・デ・サリナスがDe musica libri septem (1577) で記述した1/3コンマ中全音律では短三度が純正となる。
完全五度を狭くする量を1/4コンマよりも少なく、1/5や1/6等とした場合、長三度は純正音程よりも広くなるが、そのかわりウルフが緩和され使用に耐える調が増える。1/12ピタゴラスコンマ狭い完全五度を用いたとき、全ての完全五度は均等化され、即ちこれは十二平均律に等しい。
http://ja.wikipedia.org/wiki/%E3%83%94%E3%82%A2%E3%83%8E%E8%AA%BF%E5%BE%8Bから
ピアノ調律での
ピアノの音には倍音が含まれる。 どの鍵盤も弾いて出るその音は、基音とその倍音が多数(理論上は無限)含まれる。 ただし、現実の音の倍音は必ずしも厳密な整数倍ではなく、実際にうなりを聴いて調律した時、1オクターブ上の音をうなりが消える高さに合わせると、理論上の2倍の周波数よりも高めになる。 これを繰り返して全体の調律を行うと特にピアノの場合、高音域は理論値よりも高く、低音域はより低くなる。 この基音に対して整数倍で発生するはずの倍音が振動数が若干高く現れる現象のことをインハーモニーシティという。 インハーモニシティはピアノ1台ごとに異なるので、当然調律される各音域の絶対値も厳密には1台ごとに異なる。 この現象が起きる要因としていくつかあるが、とりわけピアノは音域が広く、また使用される弦(ミュージックワイヤー)はとても剛性が高いので振動の節になる部分が影響を受け波長が短くなるためと言われている。
ピタゴラスコンマ(英: Pythagorean comma)は、音楽用語の一つで、ピタゴラス音律が原理的にもつオクターブ関係との誤差である。ダイトニックコンマ(英: Ditonic comma)ともいう。 約23.46セント(半音の約1/4)。
ピタゴラス音律は、3:2の周波数比の音を得ることを繰り返すことに基づく音律である。しかし3/2の冪乗は2/1(オクターブ関係を規定する)の冪乗とは一致することが無いので、この操作を何回繰り返しても正確なオクターブの関係は得られない。
周波数を3/2倍する操作を12回繰り返すと (3/2)12 ≈ 129.75 となり、 27 = 128 即ち元の音の7オクターブ上の音より若干高い音になる。
正確には (3/2)12/ 27 = 312 / 219 = 531441 / 524288 の差が生じ、これをピタゴラスコンマと呼ぶ。
セント値で表すと log2(3/2)12 × 1200 ≈ 8423.46 であり、7オクターブ(8400セント)との差は約23.46セントである。
シントニックコンマ(英: syntonic comma)は音楽用語の一つで、ピタゴラス音律に現れる長三度と純正な長三度との差をいう。約21.51セント。
また、これは純正な完全五度から純正な完全四度を引いて得られる大全音(9/8)と、純正な長三度から大全音を引いて得られる小全音(10/9)の差でもある。
ピタゴラス音律の周波数を3/2倍する操作を4回繰り返した十七度の音程の比率は (3/2)4 = 81/16、これを2オクターブ下げた長三度は81/64である。一方、純正な長三度は 5/4 = 80/64 である。つまりピタゴラス音律の長三度は純正な長三度より 81/80だけ広い。これをセント値で表すと、1200 * log281/80 = 21.506289596... 即ち約21.51セントである。
ピタゴラス音律における長三度は、1200 * log281/64 = 407.820003461... セントであり、これは十二音平均律の長三度(400セント)に比べても 8 セント近く広い。純正な長三度は、1200 * log25/4 = 386.313713864... セントである。
シントニックコンマ - ピタゴラス音律の長3度(81/64)と純正な長3度(5/4)との差。約21.51セント。
平均律vs純正律シリーズ 純正律の調律を体験しよう / Structure of Perfect Intonation Tun
平均律vs純正律シリーズ 各調律法による和音聴き比べ(C-Dur基準版)
平均律vs純正律シリーズ 純正律の和音を知ろう / Just Intonation
平均律vs純正律シリーズ 波形と音で調律聞き比べ(平均律・純正律・キルンベルガー第3法)
http://ja.wikipedia.org/wiki/%E5%B9%B3%E5%9D%87%E5%BE%8Bから
平均律
十二平均律とは、1オクターヴを12等分した音律である。隣り合う音(半音)の周波数比は等しく![sqrt[12]{2}:1](http://upload.wikimedia.org/math/9/b/2/9b27d440a0b7bd84397304e94fb9aa1e.png) (100セント)となる。
(100セント)となる。
1オクターヴを12等分するという方法による十二平均律では、1度(ユニゾン)と8度(オクターヴ)を除いて簡単な整数比率による純正な音程は得られない。 その代わりピタゴラス音律や中全音律で生じる著しく誤差の大きな音程(ウルフ)によって妨げられること無く、全ての調で演奏が可能で、転調や移調が自由に行える[1]。 十二平均律では半音の大きさは均一であり、異名同音は実際に同じ音となる。また不均一な音律に由来する個々の調の性格の特異性は生じない。 十二平均律はピタゴラス音律を調整してピタゴラスコンマを全ての完全5度に均等に拡散した音律であると考えることもできる。結果、十二平均律の完全5度は純正音程から1/12ピタゴラスコンマ分狭くなっているものの、その差は比較的少ない。一方で長短の3度は、ピタゴラス音律よりは純正音程に近いが、依然として差が大きい。
平均律はギターなどのフレット式弦楽器との親和性が高い。楽器の調律において、純正な音程は2つの音を同時に出し倍音のうなりが消えるようにすることで調律できるが、平均律ではユニゾンとオクターヴ以外に純正な音程が存在しないため、鍵盤楽器などの調律は容易ではない。一方、フレット式楽器やモノコードなどでは、幾何的に弦の分割点を設定することで平均律を実現できる。またフレット式楽器では、平均律以外の半音の音程が一定でない音律では、各弦に対するフレット間隔が揃わず、直線のフレットを用いるには不都合である。
| 音程 | 十二平均律による値 | 数値 | セント値 | 純正音程 | 純正音程のセント値 | 差 |
|---|---|---|---|---|---|---|
| 一度 |  |
1.000000 | 0 | 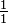 = 1.0000000 = 1.0000000 |
0.00 | 0 |
| 短二度 | ![2^{1/12} = sqrt[12]{2}](http://upload.wikimedia.org/math/1/c/3/1c323b6c1d805e260ba1ebafe180decf.png) |
1.059463 | 100 | 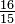 ≈ 1.06666… ≈ 1.06666… |
111.73 | −11.73 |
| 長二度 | ![2^{2/12} = sqrt[6]{2}](http://upload.wikimedia.org/math/a/2/8/a28f7edb1a398ffab8f42ac9b16dfd8d.png) |
1.122462 | 200 | 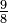 = 1.1250000 = 1.1250000 |
203.91 | −3.91 |
| 短三度 | ![2^{3/12} = sqrt[4]{2}](http://upload.wikimedia.org/math/3/6/e/36e9f319b0ea5afe47b729f08e4ad532.png) |
1.189207 | 300 |  = 1.2000000 = 1.2000000 |
315.64 | −15.64 |
| 長三度 | ![2^{4/12} = sqrt[3]{2}](http://upload.wikimedia.org/math/e/0/7/e077f20b356a38023c48f7352a304c08.png) |
1.259921 | 400 | 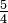 = 1.2500000 = 1.2500000 |
386.31 | +13.69 |
| 完全四度 | ![2^{5/12} = sqrt[12]{32}](http://upload.wikimedia.org/math/f/3/7/f3742e11ac225b783a4daa0c1a8350e6.png) |
1.334840 | 500 |  ≈ 1.33333… ≈ 1.33333… |
498.04 | +1.96 |
| 増四度 |  |
1.414214 | 600 | 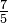 = 1.4000000 = 1.4000000 |
582.51 | +17.49 |
| 完全五度 | ![2^{7/12} = sqrt[12]{128}](http://upload.wikimedia.org/math/4/8/0/48061b5c0376c5977de2aba65b1f986d.png) |
1.498307 | 700 |  = 1.5000000 = 1.5000000 |
701.96 | −1.96 |
| 短六度 | ![2^{8/12} = sqrt[3]{4}](http://upload.wikimedia.org/math/f/5/2/f52814ec9e29d7611585d9bcd3f893fd.png) |
1.587401 | 800 | 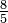 = 1.6000000 = 1.6000000 |
813.69 | −13.69 |
| 長六度 | ![2^{9/12} = sqrt[4]{8}](http://upload.wikimedia.org/math/8/5/c/85ca2708d0878b8858d1a7678c4b87a5.png) |
1.681793 | 900 |  ≈ 1.66666… ≈ 1.66666… |
884.36 | +15.64 |
| 短七度 | ![2^{10/12} = sqrt[6]{32}](http://upload.wikimedia.org/math/1/7/7/177729758c064ee402d3f2dd50fb65a8.png) |
1.781797 | 1000 |  ≈ 1.77777… ≈ 1.77777… |
996.09 | +3.91 |
| 長七度 | ![2^{11/12} = sqrt[12]{2048}](http://upload.wikimedia.org/math/b/7/8/b78c388897c48d34f37d2ae727434d6d.png) |
1.887749 | 1100 |  = 1.8750000 = 1.8750000 |
1088.27 | +11.73 |
| 八度 |  |
2.000000 | 1200 |  = 2.0000000 = 2.0000000 |
1200.00 | 0 |
中国では平均律の計算は漢代から論ぜられており、南北朝の宋の元嘉24年(447年)ころに、何承天(370年 - 447年)が平均律に近いものを算出している。明の万暦24年(1596年)には、朱載堉(1536年 - 1610年)が『律呂精義』(1584年)において、古代からの十二律に用いられた三分損益法(ピタゴラス音律)を補正して平均化するという発想から現在の平均律と同様のものに到達したが、実用化はされなかった。
朱載堉の計算方法は、まずオクターヴを平方根で2等分して増4度/減5度(3全音)を得、次いでそれを平方根で2等分して短3度(1全音と半音)を得、最後にこれを立方根で3等分して短2度(半音)を得るものだった。つまり2の十二乗根と同じものである。また朱載堉はオクターヴを9尺:4.5尺とした管長で平均律の各音を求めたが、その誤差は±0.3セント未満と、後述のステヴィン(1585年)よりも高い精度を得ている。もちろん誤差とは小数点以下を何桁まで計算するかというだけの問題であり、実質は現代の平均律と同じことである。
日本では和算家の中根元圭が「律原発揮(元禄5年、1692年)」において、1オクターヴを12乗根に開き平均律を作る方法を発表した。
インドでははっきりしないが、カルナータカ音楽(南インド古典音楽)の世界における17世紀の理論家ヴェーンカタマキーの72メーラカルタ理論は、オクターヴを12半音に分ける考え方をとっている。
ヨーロッパではまずアリストクセノス(前4世紀ごろ)が数比に依拠するピュタゴラス派の音楽理論を批判して、音律は聴覚によって判断されなければならないとし、全音を12等分してテトラコルドの分割を説明した(12等分したのは、半音、4分音と3分音を記述するためだったと推定される)。アリストクセノスはオクターヴを12等分するという意味での平均律は記述していないが、感覚的に「全音は半音2つ、全音2つと半音ひとつで完全4度」と規定した点は平均律の発想の祖といってよい。
朱載堉に次いで平均律を2の12乗根として西洋で最初に数学的に記述したのはシモン・ステヴィン(1585年)で、彼はオクターヴを10000:5000として整数比で平均律を記述した。ステヴィンの平均律の理論値からの誤差は±0.43セント未満である。後にマラン・メルセンヌ(1588年 - 1648年)は Harmonie universelle (1636年)においてオクターヴを2000000:1000000として、ほぼ完璧に平均律を記述した(従来はこのメルセンヌをもって平均律が確立されたとすることが多かった)。
リュートやギター、ヴィオラ・ダ・ガンバなどのフレット式の弦楽器においては16世紀には平均律が一般的に使用されていた可能性が高い[2]。 マルティン・アグリコラはMusica instrumentalis deudsch (1545年)で「リュート奏者やヴィオラ・ダ・ガンバ奏者の大多数は、全てのフレットを等しくする……それぞれのフレットは小半音となる」と述べている[3]。 ヴィンチェンツォ・ガリレイは『新旧音楽の対話』(1581年)の中で、半音を18:17(約99セント)とするフレット装置法を記しており、これによって実用的に十分な精度で平均律によるフレットの位置決めが可能である。また彼はリュートの音律は鍵盤楽器とは異なるとして、不均一なフレットで大小の半音を得たり、補助フレットを追加したりすることを批判している[4]。 ホアン・カルロス・アマートのギター教本『ギターラ・エスパニョーラ』(1596年)では、24のすべての調の三和音の奏し方が左手の指の押さえ方を示す図表を用いて記されており、それらに番号を振ることで任意の調における一定の和音の進行が一覧表にして示されている。また中全音律で調律されていたであろう鍵盤楽器との合奏における、音律の不一致による問題は16世紀中葉から報告されている[5]。
鍵盤楽器においても、17世紀初頭には一定の精度で、また一定の範囲で平均律が実用化されていたと主張する専門家もおり、フレスコバルディ(1583年 - 1643年)、フローベルガー(1616年 - 1667年)がすでに平均律を使用していたという説もある (Lindley 1980)。ジャン=フィリップ・ラモーは『和声の生成』(1737年)において平均律を推奨し、「任意のキーを決め、そこから正確な五度を調律し、それをほんのわずか狭くする。こうしてある五度から別の五度へ低い方から高い方へ最後の五度まで行なう」という形で実践的な調律法を述べている。ダニエル・ゴットロープ・テュルクの『クラヴィーア教本』(1789年)の記述によれば、ヨハン・フィリップ・キルンベルガーが『純正作曲の技法』(1771 - 79年)の中で、平均律は必ずしも有益ではないとして、自身の考案した不均等律(キルンベルガー第二法)を推奨した当時には、既に平均律がほぼ一般的に受け入れられていた。しかしイギリスのオルガン建造家たちは1850年頃まで平均律を用いようとしなかった[6]。
しばしば議論の対象となるヨハン・ゼバスティアン・バッハ(1685年 - 1750年)の『平均律クラヴィーア曲集』(独原題 Das Wohltemperirte Clavier )については、かつてはバッハが平均律を用いれば、オクターヴの12の音を主音とする24の長短調で作曲できることを示したものとされていた。その後、20世紀後半に古楽研究が進むにつれて中全音律をはじめとする古典調律への関心が高まり、Wohltemperirteとは『よく調整された音律』という意味であり、必ずしも平均律を意味するものではなく、むしろバッハが意図したのはヴェルクマイスターの調律法のような、全ての調が演奏可能な不均等律である、という考えが一般的となった。ただしバッハが平均律を用いていた可能性も依然として否定はできない。
20世紀に広まった無調の音楽、特に十二音技法は、全ての半音を均等に扱う平均律の性質との結び付きが強い。
現在では、平均律は標準的な音律としての地位を確立している。マリンバなどの有鍵打楽器も平均律に近い調律がなされており、電子オルガン、シンセサイザーなどの電子鍵盤楽器も平均律を基準にしているものが多い(ただし、電子楽器では近年、古典調律、さらには自由な調律法に変更可能な機能を持つものが増えている)。しかし、平均律が標準であるとはいえ、鍵盤楽器などの音高の固定された楽器を除けば、常にそれに従うわけではない。音律の設定はあらゆる楽器にとって重要なこととは限らない。声楽はもちろんヴァイオリンなどのフレットの無い弦楽器や、金管楽器などでは、演奏時に奏者の様々な微調節が行われることが多い。ギターなどフレットを備えた弦楽器や、音孔を備えた木管楽器でも弦の押さえ方やアンブシュア等奏法上の工夫で調節がなされる。
コメントが来たので。
ビートルズについては、逆回しで再生した時に、サブリミナル的にいろいろとメッセージが入っているという記事で説明しました。検索すると沢山出てきます。
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1017870710から
先ず、ドレミファソラシドが何故成立したのか
を考える必要がありますね。
ミとファ、シとドの間だけ半音、後は全音に
なっている(平均律の場合)。
純正律と平均律の前に、ピタゴラス音階と言う物がありました。
音楽の一番最初の形は勿論、原始的な歌であったでしょうが、
楽器も考えられた。
最初は遠くの仲間を呼ぶ笛とかであったでしょう。
さて、笛では、長さによって音の波長、即ち振動数が変わる。
ドの倍の周波数(波長は半分)は1オクターヴ上のドです。
しかし、ドの3倍は1オクターヴ半上のソになります。
そのソの3倍はレ、レの3倍はラ、ラの3倍はミ、ミの3倍はシ、
シの3倍はファ、ファの3倍はドになります。
これらを1オクターヴに持ってきたものが(つまりドの3倍のソならば、
更に1/2にして最初のドと2倍のドの間に持ってくる)
ピタゴラス音階です。
最初のドの周波数を1とすれば、ドレミファソラシドの周波数は
1,9/8,81/64,4/3,3/2,27/16,243/128,2
となります。
これはかなりミとファ、シとドの間だけが半音で、後は全音、に近い。
しかし少し違う。
この音階の響きはなかなか良くても移調をする際に本質的な問題を引き起こす、
例えばハ長調をヘ長調に移調する際、違う音階になってしまうのです。
そこで平均律の考えが出てきました。
半音、全音の感覚は、ピタゴラス音階でもかなり分かる、そこで1オクターヴを
12音の半音で均等に割ろう、
勿論、人間の耳と言うのは、1次関数で聴こえるように出来ていない、
等比数列的に聴こえるように出来ている。
ド♯を2の12乗根、レを2の2乗の12乗根、レ♯を2の3乗の12乗根、・・・
と言うようにします。
勿論これで1オクターヴ上のドは、2の12乗の12乗根=2となり合いますし、
人間の耳にもちょうど等間隔に聴こえる。
これで、移調は自由自在になったわけです。
しかし、平均律は12乗根などと言う物をとりますから、綺麗に協和した音程は
1オクターヴ上とか下とか、その他同じドならド以外、一つもありません。
我々は平均律に慣らされていまして、十分美しく聴こえます。
しかし厳密には物理で習ううなりが聴こえ、
ピアノの調律師の方など、器具も使いますが、そのうなりの回数で調律しています。
さて、美しいハーモニーを得るにはどうするか。
出来るだけ単純な周波数の比になるよう、音階を構成すればいい。
そこで考え出されたのが純正律です。
これはドを1、1オクターヴ上のドを2にしたとき、ドレミファソラシドが
1,9/8,5/4,4/3,3/2,5/3,15/8,2
になる物です。
ピタゴラス音階でも、特に完全5度は美しい音程とされてきました。
しかし、歴史が進むにつれ、3度の和音が重要視されるようになって
来ました。
ピタゴラス音階では3度(ドーミ)は1:81/64と余り単純でない。
純正律では1:5/4とかなり単純で綺麗なハーモニーに聴こえます。
これくらいの説明でどうでしょうか?
P.S.かなり簡単にしましたが、それでも分かりにくかったですか?
平均律の説明で少し数学用語を使っているからですかね?
周波数倍が1オクターヴです。あるドの2倍の周波数は1オクターヴ上のドです。
その2倍、つまり元のドからすれば、4倍の周波数が2オクターヴ上のドです。
その2倍、つまり元のドからすれば、8倍の周波数が3オクターヴ上のドです。
このように、人間の耳では周波数比で言うと、1:2:4:8が同じドに聴こえるのです。
中学の数学を思い出していただければ、等比数列
2の0乗=1、2の1乗=2、2の2乗=4、2の3乗=8で、
人間は1:2:4:8が等間隔に聴こえる、
元、1オクターヴ上、2オクターヴ上、3オクターヴ上、に聴こえるのです。
そうするとオクターヴ内を割るのも、1,2,4,8と倍々でオクターヴを作っていったように、
ドとドの♯とレとレの♯とミとファと・・・も等比数列になる必要がある。
ドの1オクターヴ上のドは周波数2倍。これは絶対。
そうすると等比数列になるには12等分ではいけない。
ドに何かをかけてドの♯、ドの♯に何かをかけてレ、
レに何かをかけてレの♯、の何かが全て同じでないといけない。
12回かけて周波数2倍になるのだから、その何かは2の12乗根。
2の12乗根とは、そのまま12回かけて2になる数です。.
だから、ドを1として、ドの♯は1×2の12乗根で2の12乗根、
レはそれに更に2の12乗根をかけて、2の12乗根×2の12乗根
=2の2乗の12乗根、
レの♯は更に2の12乗根をかけて、2の3乗の12乗根・・・
という事です。
P.S.2
まだわかりにくいですか?
何処が分かりにくいか仰ってもらえば答えますよ。
中学の数学の教科書も見てください。
P.S.3
まだお分かりにならない、単に知恵袋を見ていなかったり、
BAを選んでないだけですかね?
猿には分かりませんが、中学生にはわかるように説明したんですが。
平均律には数式があります。
純正律は平均律に似た感じで、周波数比が単純になる物を
選んだだけです。
実際純正律の3度は平均律より1/12音ほど低いです。
http://onkan.exinfo.biz/750/post_37.htmlから
正律とは、「ドミソ」、「ファラド」、「ソシレ」の主要3和音が綺麗に響くように、1オクターブの中に「ドレミファソラシ」の音程を並べる方法をいいます。
具体的には、まず、下記のようにソの音とファの音(主要3和音の一番下の音)を調律します。
その後、他の音も、「ド」、「ファ」、「ラ」を基準として純正3度または純正5度の関係になるように調律をしていきます。
このようにして、「ドレミファソラシ」の音程を並べた音律を純正律といいます。
純正率の特徴は、下記のような点になります。
http://ja.wikipedia.org/wiki/%E3%83%94%E3%82%BF%E3%82%B4%E3%83%A9%E3%82%B9%E9%9F%B3%E5%BE%8Bから
ピタゴラス音律(ピタゴラスおんりつ)は、3:2の周波数比の関係にある音程を基に作られる音律である。ピタゴラスが発案したという伝説により、この名がある。
ピタゴラス音律は3:2の比率の完全五度の音程を積み重ねることに基づいている。例としてDを起点に、上に6回、下に5回、3:2の周波数比の音を得ることを繰り返すと以下のようになる。
E♭ - B♭ - F - C - G - D - A - E - B - F# - C# - G#
得られた11個の音は実際には広い音域に渡っているが、オクターヴ関係にある音には同じ音名が与えられることから、絶対音高を移し変えて、これらを1オクターヴの範囲内にまとめることができる。
この作業を更に拡張しようとすると問題が浮上する。即ちオクターヴの比率は2:1であるが、3/2の冪乗は2/1の冪乗と一致することはないため、この操作を何回繰り返しても互いにオクターヴ関係にある音は得られない。下方に延長した場合以下のようになる。
A♭ - E♭ - B♭ - F - C - G - D - A - E - B - F# - C# - G#
平均律においてはA♭とG♯のような異名同音は実際に全く同じ音であるが、このA♭とG♯には約23.46セント≒1/4半音の差が生じる。この差をピタゴラスコンマと呼ぶ。
したがって、半音階を構成する際に、A♭を省いてE♭からG♯までの12音を用いると、G♯からE♭への五度音程は、3:2の比率による純正な完全五度(約701.96セント)よりピタゴラスコンマ分狭い音程(約678.49セント)になる。この音程の外れた五度による和音は、顕著なうなりを生じるため、狼の吠声に例えてウルフの五度(en:Wolf interval)と呼ばれる。
どの音を起点にするか、上下にどの様に完全五度を積み重ねるかは自由である。したがってウルフの五度の位置は自由に決められる。しかしいずれかの五度にウルフが住むため、ピタゴラス音律では演奏可能な調は制限される。
| 音名 | Dからの音程 | 計算式 | 比率 | 大きさ (セント) | 平均律との差 (セント) |
|---|---|---|---|---|---|
| A♭ | 減五度 |  |
 |
588.27 | -11.73 |
| E♭ | 短二度 | 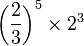 |
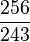 |
90.22 | -9.78 |
| B♭ | 短六度 |  |
 |
792.18 | -7.82 |
| F | 短三度 | 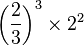 |
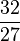 |
294.13 | -5.87 |
| C | 短七度 |  |
 |
996.09 | -3.91 |
| G | 完全四度 | 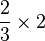 |
 |
498.04 | -1.96 |
| D | 一度 |  |
 |
0 .00 | 0.00 |
| A | 完全五度 |  |
 |
701.96 | 1.96 |
| E | 長二度 |  |
 |
203.91 | 3.91 |
| B | 長六度 |  |
 |
905.87 | 5.87 |
| F♯ | 長三度 |  |
 |
407.82 | 7.82 |
| C♯ | 長七度 |  |
 |
1109.78 | 9.78 |
| G♯ | 増四度 |  |
 |
611.73 | 11.73 |
| 音名 | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 比率 | 1/1 | 9/8 | 81/64 | 4/3 | 3/2 | 27/16 | 243/128 | 2/1 | ||||||||
| 間隔 | - | 9/8 | 9/8 | 256/243 | 9/8 | 9/8 | 9/8 | 256/243 | - | |||||||
ピタゴラス音律では異名同音的音程は異なる大きさを持つ。表に上記の12の音からの各音程の周波数比率とおおよそのセント値を示す。
その定義上、ピタゴラス音律の11の完全五度は3:2すなわち約701.955セントである。五度圏を閉じるためには、平均律がそうであるように、12の完全五度の平均値は700セントであることが要求されるため、 残る1つは約678.495セントになる(ウルフの五度)。このウルフの五度は異名同音による五度であるため、より正確には減六度である。
つまりピタゴラス音律では、異名同音的音程にはピタゴラスコンマ(約23.46セント)分の差が存在する。
またピタゴラス音律では純正な長三度(5:4≒386.31セント)は得られないが、4つの減四度が純正な長三度と僅差になる。これはピタゴラス音律の長三度と純正な長三度の差であるシントニックコンマ(約21.51セント)とピタゴラスコンマ(約23.46セント)の値がごく近いことによる結果である。
http://ja.wikipedia.org/wiki/%E7%B4%94%E6%AD%A3%E5%BE%8Bから
純正律(じゅんせいりつ Just intonation)は、周波数の比が単純な整数比である純正音程のみを用いて規定される音律である。
例えば純正律による長調の全音階は、純正完全5度(3/2)と純正長3度(5/4)を用いて各音が決定される。 すなわち、Cを基準とした場合、Cの3度上がE、5度上がG、次にGの3度上がB、5度上がD、さらにCの5度下がF、Fの3度上がAとなり、これらを1オクターヴ内に配列することでハ長調の全音階が得られる。
上述の音階を以下に示す。大文字のTは大全音(9/8)、小文字のtは小全音(10/9)、sは半音(16/15)の音程を表す。
| Note | Name | C | D | E | F | G | A | B | C | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ratio | 1/1 | 9/8 | 5/4 | 4/3 | 3/2 | 5/3 | 15/8 | 2/1 | |||||||||
| Cents | 0 | 204 | 386 | 498 | 702 | 884 | 1088 | 1200 | |||||||||
| Step | Name | T | t | s | T | t | T | s | |||||||||
| Ratio | 9/8 | 10/9 | 16/15 | 9/8 | 10/9 | 9/8 | 16/15 | ||||||||||
| Cents | 204 | 182 | 112 | 204 | 182 | 204 | 112 | ||||||||||
純正律の長所は、倍音のうなりを伴わない、単純な整数比による純正な和音が得られることである。 上記の例であれば、C-E-G、F-A-C、G-B-Dの三和音は4:5:6の比となり、三和音として最も単純な比を持つ。
短所は、音の組によっては、純正音程から著しく外れることである。上記の例ではD-Aの音程は純正完全5度(3/2)よりも81/80(シントニックコンマ)狭い40/27となり、この音程を含む和音は非常に響きが悪くなる。そのため純正律では転調や移調が困難である。
もう一つの短所は、旋律の演奏に際しては、純正律では大全音(9/8)と小全音(10/9)の2種類の全音が存在するため、音階が不均等な印象を与え、また演奏が難しいことである。
http://saigaijyouhou.com/blog-entry-2893.htmlから







http://saigaijyouhou.com/blog-entry-2896.htmlから

http://saigaijyouhou.com/blog-entry-2898.htmlから
新宿コマ劇場前で女子大生が集団昏倒する異常事態!明大公認のサークルと見られるが、男子だけは倒れず!お酒?薬物使用? new!!
