算額（その862）改訂版

算額（その862）改訂版

算額（その862）は依拠した図が間違っているので，改訂版を書いた。

二十六　岩手県一関市萩荘 赤萩観音寺前額 弘化4年(1847)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

今有如図 03034
https://w.atwiki.jp/sangaku/pages/307.html

キーワード：円8個，外円，菱形
#Julia, #SymPy, #算額, #和算

問：今有全円内如図設稜形容大円一个中円四个小円二个其小円径若干問得全円径術如何

全円の中に菱形 1 個，大円 1 個，中円 4 個，小円 2 個を容れる。小円の直径が与えられたとき，全円の直径を求めるすべを述べよ。

本問は，以下の 2 つを合わせたものである。
- 算額（その237）：大円の中に中円，小円が 2 個ずつ
- 算額（その445）：全円の中に大円 1 個，中円 2 個，菱形 1 個

山村の図は間違っている。これでは「中円 2 個，小円 4 個になってしまう。筆者も山村の図のみで算額を解いたので，なぜこのような初歩的なミスをしたのかと他人を責めることはできない。

「今有如図」は正しい図を示している。

そこで，改訂版を書くことになった。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
中円の半径と中心座標を r2, (0, R - r2), (0, R - 3r2), (x2, y2)
小円の半径と中心座標を r3, (r1 - r3, R - r1)
菱形の対角線の長い方を 2a
ただし，r1 = 2r2
とおき，以下の連立方程式を解く。

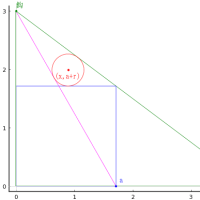
1.　大円の中に中円，小円が 2 個ずつ

以下のように，r2 = 3r3/2 である。
小円の直径が 1 のとき，中円の直径は 1.5 である。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive
r1 = 2r2
eq1 = (r1 - r3)^2 + r2^2 - (r2 + r3)^2
res = solve(eq1, r2)[1]
res |> println
res(r3 => 1//2) |> println

    3*r3/2
    3/4

2.　全円の中に大円 1 個，中円 2 個，菱形 1 個

この場合，大円の中に中円，小円があることは考えない（考えなくてよい）。したがって，r3 は方程式内に出てこない。

@syms R::real, r1::positive,
      r2::positive, x2::positive, y2::negative,
      r3::positive, x3::positive, a::positive, b::positive
r1 = 2r2
eq2 = x2^2 + (R - r1 - y2)^2 - (r1 + r2)^2
eq3 = x2^2 + y2^2 - (R - r2)^2
eq4 = dist2(0, R - 2r1, sqrt(R^2 - r1^2), -r1, x2, y2, r2);
# res2 = solve([eq2, eq3, eq4], (x2, y2, R))

一度には解けないので，まず eq2, eq3 から x2, y2 を求める。

res2 = solve([eq2, eq3], (x2, y2))[1]  # 1 of 2

    (-2*sqrt(2)*r2*sqrt(-R*(-R + 3*r2))/(-R + 2*r2), (-R^2 + 3*R*r2 + 2*r2^2)/(-R + 2*r2))

eq4 に前段で得られた x2, y2 を代入し，R について解く。

ノウハウ：式が因数分解できるときは，因数分解してから方程式を解くほうがはるかに実行速度が速い。あるいは，因数が簡単な場合には，筆算で答えを出せる。今の場合，(-3*R + 10*r2) という因数があるので，暗算で　R = r2*(10/3) であることがわかる。残りの 2 つの解は虚数解である。

eq14 = eq4(x2 => res2[1], y2 => res2[2]) |> simplify |> numerator |> factor
eq14 |> println

    r2^2*(-3*R + 10*r2)*(-5*R^2 + 8*R*r2 + 20*r2^2 - 4*sqrt(2)*sqrt(R^2 - 4*r2^2)*sqrt(R^2 - 3*R*r2))

@time ans_R = solve(eq14, R)[1]  # 1 of 4
ans_R |> println

     20.539353 seconds (10.36 k allocations: 222.250 KiB)
    10*r2/3

前節で，r2 = 3*r3/2 であったので，これを代入すると R = 5r3 となる。

ans_R(r2 => 3r3/2) |> println

    5*r3

小円の直径が 1 寸のとき，全円の直径は 5 寸となり，術に一致する。

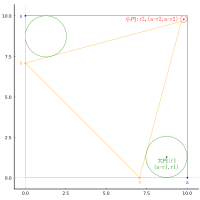
function draw(r3, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    r2 = 3r3/2
    r1 = 2r2
    R = 5r3
    (x2, y2) = (-2*sqrt(2)*sqrt(R)*r2*sqrt(R - 3*r2)/(-R + 2*r2), (-R^2 + 3*R*r2 + 2*r2^2)/(-R + 2*r2))
    a = sqrt(R^2 - r1^2)
    plot([0, a, 0, -a, 0], [-R, -r1, R - 2r1, -r1, -R], color=:blue, lw=0.5)
    circle(0, 0, R, :magenta)
    circle(0, R - r1, r1, :green)
    circle(0, R - r2, r2)
    circle(0, R - 3r2, r2)
    circle2(r1 - r3, R - 2r2, r3, :orange)
    circle2(x2, y2, r2)
    if more
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(0, R, "R", :magenta, :center, :bottom, delta=delta)
        point(0, R - r1, "大円:r1\n(0,R-r1)", :green, :center, delta=-delta)
        point(0, R - r2, "中円:r2\n(0,R-r2)", :red, :center, delta=-delta)
        point(x2, y2, "中円:r2\n(x2,y2)", :red, :center, delta=-delta)
        point(r1 - r3, R - r1, "小円:r3\n(r1-r3,R-r1)", :orange, :center, :bottom, delta=delta)
        point(0, R - 2r1, "R-2r1", :blue, :center, :bottom, delta=delta)
        point(0, -r1, "-r1", :blue, :center, :bottom, delta=delta)
    end
end;

draw(1/2, true)