算額（その1526）

算額（その1526）

三十三　岩手県一関市舞川相川 菅原神社 嘉永3年(1850)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

今有如図 03040
https://w.atwiki.jp/sangaku/pages/193.html

キーワード：円1個，直角三角形，正方形，斜線
#Julia, #SymPy, #算額, #和算

直角三角形の中に直角三角形と斜線を 1 本容れ，隙間に円を容れる。直角三角形の直角を挟む二辺（鈎，股）が 3 寸，4 寸のとき，円の直径はいかほどか。

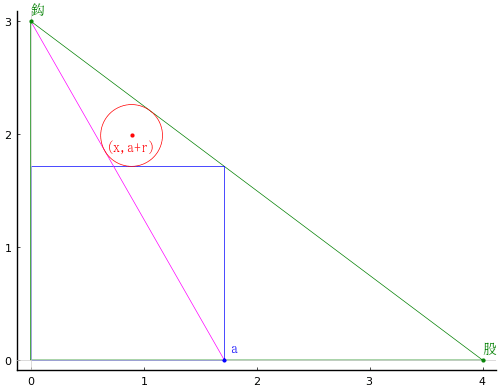
鈎，股をそのまま「鈎」，「股」
正方形の一辺の長さを a
円の半径と中心座標を r, (x, a + r)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms 鈎::positive, 股::positive, a::positive,
      r::positive, x::positive
eq1 = dist2(0, 鈎, a, 0, x, a + r, r)
eq2 = dist2(0, 鈎, 股, 0, x, a + r, r)
eq3 = (鈎 - a)/a - 鈎/股;

一度には解けないので，まず a, x を求め，次に r を求める。

res = solve([eq3, eq1], (a, x))[2]

    (股*鈎/(股 + 鈎), (-r*股^2 - r*股*鈎 + r*股*sqrt(2*股^2 + 2*股*鈎 + 鈎^2) + r*鈎*sqrt(2*股^2 + 2*股*鈎 + 鈎^2) + 股*鈎^2)/(股^2 + 2*股*鈎 + 鈎^2))

eq2 に a, x の解を代入し，その式を r について解く。

eq12 = eq2(a => res[1], x => res[2]) |> simplify |> numerator;
res = solve(eq12, r)[1];  # 1 of 2

@syms d
ans_r = apart(res, d) |> simplify
ans_r |> println

    鈎*(-股^3 + 2*股^2*鈎 + 股^2*sqrt(股^2 + 鈎^2) + 股^2*sqrt(2*股^2 + 2*股*鈎 + 鈎^2) + 2*股*鈎^2 + 股*鈎*sqrt(股^2 + 鈎^2) - 股*鈎*sqrt(2*股^2 + 2*股*鈎 + 鈎^2) - 股*sqrt(2*股^4 + 2*股^3*鈎 + 3*股^2*鈎^2 + 2*股*鈎^3 + 鈎^4) + 鈎^3 - 鈎*sqrt(2*股^4 + 2*股^3*鈎 + 3*股^2*鈎^2 + 2*股*鈎^3 + 鈎^4))/(2*(3*股^3 + 5*股^2*鈎 - 2*股^2*sqrt(2*股^2 + 2*股*鈎 + 鈎^2) + 3*股*鈎^2 - 2*股*鈎*sqrt(2*股^2 + 2*股*鈎 + 鈎^2) + 鈎^3))

円の半径を求める式は長いが，具体的な鈎，股の値を代入すれば，円の直径が求まる。

2ans_r(鈎 => 3, 股 => 4).evalf() |> println

    0.547208709287844

鈎 = 3, 股 = 4 のとき，円の直径は 0.547208709287844 である。

プログラム的には，弦，s を一時変数として若干簡単に書くことができる。

function get_r(鈎, 股)
    弦 = sqrt(股^2 + 鈎^2)
    s = sqrt(2股^2 + 2股*鈎 + 鈎^2)
    r = 鈎*(-股^3 + 2股^2*鈎 + 股^2*弦 + 股^2*s + 2股*鈎^2 + 股*鈎*弦 - 股*鈎*s - 股*弦*s + 鈎^3 - 鈎*弦*s)/
        (2*(3股^3 + 5股^2*鈎 - 2股^2*s + 3股*鈎^2 - 2股*鈎*s + 鈎^3))
    println("円の直径 = $(2r)")
    return r
end
get_r(3, 4);

    円の直径 = 0.5472087092878442

術は 以下のように，簡約化されたものである。

function 術(鈎, 股)
    弦 = sqrt(鈎^2 + 股^2)
    天 = (sqrt((鈎 + 股)^2 + 股^2)*鈎 + (鈎 + 股)*弦+股^2)*(鈎 + 股)
    r = 股^2*鈎^2/天
    println("円の直径 = $(2r)")
end;
術(3, 4)

    円の直径 = 0.5472087092878439

function draw(鈎, 股, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
    弦 = sqrt(股^2 + 鈎^2)
    s = sqrt(2股^2 + 2股*鈎 + 鈎^2)
    r = get_r(鈎, 股)
    (a, x) = (股*鈎/(股 + 鈎), (-r*股^2 - r*股*鈎 + r*股*s + r*鈎*s + 股*鈎^2)/(股^2 + 2股*鈎 + 鈎^2))
    plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
    rect(0, 0, a, a, :blue)
    segment(0, 鈎, a, 0, :magenta)
    circle(x, a + r, r)
    if more        
        delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
        hline!([0], color=:gray80, lw=0.5)
        vline!([0], color=:gray80, lw=0.5)
        point(股, 0, "股", :green, :left, :bottom, delta=delta)
        point(0, 鈎, "鈎", :green, :left, :bottom, delta=delta)
        point(a, 0, " a", :blue, :left, :bottom, delta=delta)
        point(x, a + r, "(x,a+r)", :red, :center, delta=-delta)
    end
end;

draw(3, 4, true)