算額（その224）

算額（その224）

中村信弥「改訂増補 長野県の算額」
http://www.wasan.jp/zoho/zoho.html
県内の算額3（201）
長野県北佐久郡軽井沢町峠 熊野神社 安政4年(1857)

扇の面に大円，中円，小円が描かれている。扇の要から先端まで（扇骨の長さ）が 7寸9分6厘，大円の径が 5寸9分7厘であるとき，中円の径を求めよ。

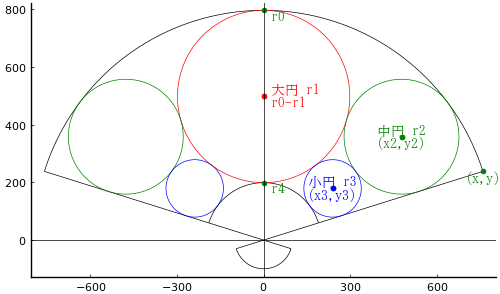
図のように記号を定める。
扇面の外周円の半径（扇骨の長さ）を r0
要から扇の紙がはられていない部分の半径（図参照）を r4
大円の半径，中心座標を r1, (0, r0 - r1)
中円の半径，中心座標を r2, (x2, y2)
小円の半径，中心座標を r3, (x3, y3)
扇の右端の点（図参照）の座標を (x, y) とする。
ただし，r0 = 798, r1 = 597, r4 = r0 - 2r1 である。また，y = sqrt(r0^2 - x^2) である。 

以下の連立方程式を立て，nlsolve() で数値解を求める。

using SymPy

function distance(x1, y1, x2, y2, x0, y0)
   p1, p2 = sympy.Point(x1, y1), sympy.Point(x2, y2)
   l = sympy.Line(p1, p2)
   l.distance(sympy.Point(x0, y0))^2  # 二乗距離を返す！！
end;

@syms r0::positive, r1::positive, r2::positive, r3::positive, r4::positive,
   x2::positive, y2::positive, x3::positive, y3::positive, x::positive, y::positive;

r0 = 796
r1 = 597 // 2
r4 = r0 - 2r1
y = sqrt(r0^2 - x^2)
eq1 = x3^2 + y3^2 - (r3 + r4)^2
eq2 = (x2 - x3)^2 + (y2 - y3)^2 - (r2 + r3)^2
eq3 = x3^2 + (r0 - r1 - y3)^2 - (r1 + r3)^2
eq4 = x2^2 + (r0 -r1 - y2)^2 - (r1 + r2)^2
eq5 = x2^2 + y2^2 - (r0 - r2)^2
eq6 = distance(0, 0, x, y, x2, y2) - r2^2
eq7 = distance(0, 0, x, y, x3, y3) - r3^2;

# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7])

println(eq1, ",")
println(eq2, ",")
println(eq3, ",")
println(eq4, ",")
println(eq5, ",")
println(eq6, ",")
println(eq7, ",")

   x3^2 + y3^2 - (r3 + 199)^2,
   -(r2 + r3)^2 + (x2 - x3)^2 + (y2 - y3)^2,
   x3^2 + (995/2 - y3)^2 - (r3 + 597/2)^2,
   x2^2 + (995/2 - y2)^2 - (r2 + 597/2)^2,
   x2^2 + y2^2 - (796 - r2)^2,
   -r2^2 + x^2*(x*y2 - x2*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x2 + y2*sqrt(633616 - x^2))/633616 + x2)^2,
   -r3^2 + x^2*(x*y3 - x3*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x3 + y3*sqrt(633616 - x^2))/633616 + x3)^2,

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=1e-14)
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=1e-14)
       v = r.zero
   end
   return v, r.f_converged
end;

function H(u)
   (r2, x2, y2, r3, x3, y3, x) = u
   return [
       x3^2 + y3^2 - (r3 + 199)^2,
       -(r2 + r3)^2 + (x2 - x3)^2 + (y2 - y3)^2,
       x3^2 + (995/2 - y3)^2 - (r3 + 597/2)^2,
       x2^2 + (995/2 - y2)^2 - (r2 + 597/2)^2,
       x2^2 + y2^2 - (796 - r2)^2,
       -r2^2 + x^2*(x*y2 - x2*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x2 + y2*sqrt(633616 - x^2))/633616 + x2)^2,
       -r3^2 + x^2*(x*y3 - x3*sqrt(633616 - x^2))^2/401469235456 + (-x*(x*x3 + y3*sqrt(633616 - x^2))/633616 + x3)^2,
   ]
end;

iniv = [big"300.0", 400, 500, 150, 100, 100, 700]
res = nls(H, ini=iniv)

   (BigFloat[199.0000000000000000000000000000000000003059242582377957862817582029431903187704, 477.6000000000000000000000000000000000001229072112677520304477397424728031693592, 358.1999999999999999999999999999999999993269666318768492701801319535249814981402, 99.49999999999999999999999999999999999969321045225668210052457642746139024754251, 238.7999999999999999999999999999999999995707652750100779995615047089452401612384, 179.100000000000000000000000000000000000061357909548663579895084714507721987446, 759.5807976794579513846102530511571579906945490238112350429439611428561425365724], true)

using Printf
(a1, a2, a3, a4, a5, a6, a7) = res[1]
@printf("r2 = %.3f,  x2 = %.3f;  y2 = %.3f; r3 = %.3f;  x3 = %.3f;  y3 = %.3f; x = %.3f\n",
           a1, a2, a3, a4, a5, a6, a7)

   r2 = 199.000,  x2 = 477.600;  y2 = 358.200; r3 = 99.500;  x3 = 238.800;  y3 = 179.100; x = 759.581

r2 = 199.000;  x2 = 477.600;  y2 = 358.200
r3 =  99.500;  x3 = 238.800;  y3 = 179.100
r4 = 199.000;   x = 759.581;   y = 238.019
中円の径 = 2r2 = 398.000
小円の径 = 2r3 = 199.000

中円の直径は 398 寸である。

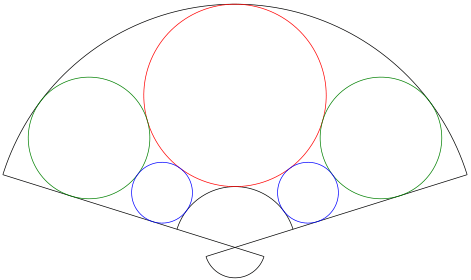
using Plots
using Printf

function circle(ox, oy, r, color=:red; beginangle=0, endangle=360, fill=false)
   θ = beginangle:0.1:endangle
   x = r.*cosd.(θ)
   y = r.*sind.(θ)
   if fill
       plot!(ox .+ x, oy .+ y, linecolor=color, linewidth=0.5, seriestype=:shape, fillcolor=color)
   else
       plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
   end
end;

function circle4(x, y, r, color=:red)
  circle(x, y, r, color)
  circle(x, -y, r, color)
  circle(-x, y, r, color)
  circle(-x, -y, r, color)
end;

function point(x, y, string="", color=:green, position=:left, vertical=:top; mark=true)
   mark && scatter!([x], [y], color=color, markerstrokewidth=0)
   annotate!(x, y, text(string, 10, position, color, vertical))
end;

function segment(x1, y1, x2, y2, color=:black; linestyle=:solid, linewidth=0.5)
   plot!([x1, x2], [y1, y2], color=color, linestyle=linestyle, linewidth=linewidth)
end;

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, x2, y2, r3, x3, y3, x) = res[1]
   r0 = 796
   r1 = 597//2
   r4 = r0 - 2r1
   y = sqrt(r0^2 - x^2)
   @printf("r2 = %.3f;  x2 = %.3f;  y2 = %.3f\nr3 =  %.3f;  x3 = %.3f;  y3 = %.3f\nr4 = %.3f;   x = %.3f;   y = %.3f\n",
           r2, x2, y2, r3, x3, y3, r4, x, y)
   @printf("中円の径 = 2r2 = %.3f\n小円の径 = 2r3 = %.3f\n", 2r2, 2r3)
   deg = atand(y/x)
   plot()
   circle(0, 0, r0, :black, beginangle=deg, endangle=180 - deg)
   circle(0, 0, r4, :black, beginangle=deg, endangle=180 - deg)
   circle(0, 0, r4/2, :black, beginangle=180 + deg, endangle=360 - deg)
   factor = r4/2 / r0
   segment(x, y, -x*factor, -y*factor)
   segment(-x, y, x*factor, -y*factor)
   circle(0, r0 - r1, r1)
   circle(x2, y2, r2, :green)
   circle(-x2, y2, r2, :green)
   circle(x3, y3, r3, :blue)
   circle(-x3, y3, r3, :blue)
   if more == true
       point(x, y, "(x,y)")
       point(0, r0 - r1, " 大円 r1", :red, :left, :bottom)
       point(0, r0 - r1, " r0-r1", :red)
       point(0, r0, " r0")
       point(0, r4, " r4")
       point(x2, y2, "(x2,y2)", :green, :center)
       point(x2, y2, "中円 r2", :green, :center, :bottom)
       point(x3, y3, "(x3,y3)", :blue, :center)
       point(x3, y3, "小円 r3", :blue, :center, :bottom)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;