算額（その1129）

算額（その1129）

依拠した図が間違っているので，算額（その1129）改訂版を書いた。

四十五 岩手県一関市真滝 熊野白山滝神社 明治13年(1880)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円4個，長方形，斜線2本

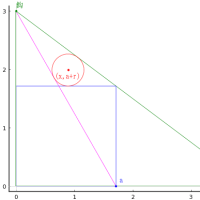
長方形内に斜線を 2 本引き，大円 1 個，中円 1 個，小円 2 個を容れる。小円の直径が 1 寸のとき，大円の直径はいかほどか。

長方形の長辺，短辺を a, b
斜線と長方形の辺の交点座標を (c, 0), (0, d)
大円の半径と中心座標を r1, (r1, r1)
中円の半径と中心座標を r2, (a - r2, r2)
小円の半径と中心座標を r3, (r3, b - r3), (a - r3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt")

using SymPy

@syms a::positive, b::positive, c::positive, d::positive,
     r1::positive, r2::positive, r3::positive, y3::positive
eq1 = dist2(c, 0, a, b, r1, r1, r1)/b
eq2 = dist2(c, 0, a, b, a - r2, r2, r2)/b |> factor |> (x -> x/(a - c))
eq3 = dist2(c, 0, a, b, a - r3, y3, r3) |> factor |> (x -> x/(a - c)) # 長い。次の式で代替
eq4 = dist2(0, d, a, b, r1, r1, r1)/a
eq5 = dist2(0, d, a, b, r3, b - r3, r3)/a |> factor |> (x -> x/(b - d))
eq6 = (b - d) + a - sqrt((b - d)^2 + a^2) - 2r3;
eq7 = r3*(b - r2) - r2*(b - y3)
eq8 = (r2 - r3)^2 + (y3 - r2)^2 - (r2 + r3)^2 |> expand;

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, b, c, d, r1, r2, y3) = u
   return [
2*a*c*r1 - 2*a*r1^2 + b*c^2 - 2*b*c*r1 - 2*c^2*r1 + 2*c*r1^2,  # eq1
a*b - 2*a*r2 - b*c - 2*b*r2 + 2*c*r2 + 2*r2^2,  # eq2
a*d^2 - 2*a*d*r1 + 2*b*d*r1 - 2*b*r1^2 - 2*d^2*r1 + 2*d*r1^2,  # eq4
a*b - a*d - 2*a*r3 - 2*b*r3 + 2*d*r3 + 2*r3^2,  # eq5
a + b - d - 2*r3 - sqrt(a^2 + (b - d)^2),  # eq6
-r2*(b - y3) + r3*(b - r2),  # eq7
r2^2 - 4*r2*r3 - 2*r2*y3 + y3^2,  # eq8
   ]
end;

r3 = 1/2
iniv = BigFloat[7.1, 5.9, 4.6, 4.8, 2.6, 0.6, 1.8]
res = nls(H, ini=iniv)

   ([7.027136940056593, 6.873446923486708, 5.683867530253209, 5.790488795112855, 3.1170295710670763, 0.6066212648596468, 1.7080941559102136], true)

初期値により解がかなり変動する。いずれの場合もちゃんと収束はしている。
しかし，どの場合も大円の直径は6前後である。
「答」のように「大円径三寸」はありえない。図を見ても明らかであろうに。

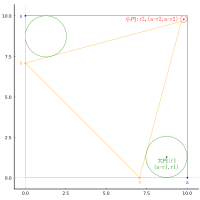
小円の直径が 1 のとき，大円の直径は 6.23406 である。
r3 = 0.5;  a = 7.02714;  b = 6.87345;  c = 5.68387;  d = 5.79049;  r1 = 3.11703;  r2 = 0.606621;  y3 = 1.70809

function draw(r3, more=false)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, c, d, r1, r2, y3) = res[1]
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r3, 2r1)
   @printf("r3 = %g;  a = %g;  b = %g;  c = %g;  d = %g;  r1 = %g;  r2 = %g;  y3 = %g\n", r3, a, b, c, d, r1, r2, y3)
   #(a, b, c, d, r1, r2, y3) = [85, 80, 40, 55, 28, 14, 40]./16
   plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:green, lw=0.5)
   segment(0, d, a, b)
   segment(c, 0, a, b)
   circle(r1, r1, r1, :blue)
   circle(a - r2, r2, r2, :magenta)
   circle(r3, b - r3, r3, :orange)
   circle(a - r3, y3, r3, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
   end
end;