算額（その1356）

算額（その1356）

十七 群馬県高崎市八幡町 八幡宮 文化7年(1810)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円3個，等脚台形
#Julia, #SymPy, #算額, #和算

等脚台形（梯形）の中に大円 1 個，小円 2 個を容れる。大円の直径が 7 寸，大頭（下底）が  18 寸と 2/3 のとき，小円の直径はいかほどか。

等脚台形の下底，上底を 2a, 2b，高さを h
大円の半径と中心座標を r1, (0, r1)
小円の半径と中心座標を r2, (r2, h - r2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, h::positive, r1::positive, r2::positive
#(r1, a) = (14//2, (18 + 2//3)//2)
eq1 = dist2(b, h, a, 0, r2, h - r2, r2)
eq2 = dist2(b, h, a, 0, 0, r1, r1)
eq3 = r2^2 + (h - r1 - r2)^2 - (r1 + r2)^2;
# res = solve([eq1, eq2, eq3], (r2, b, h))

SymPy の性能上，一度には解けないので，eq1, eq2 を解いて，h, b を求め，その解を eq3 に代入して r2 について解く。

res = solve([eq1, eq2], (h, b))[1]  # 1 of 2

   (2*r1*(a^2 - a*r2 - r1*r2)/(a^2 - r1^2), r2*(a + r1)/a)

eq13 = eq3(h => res[1])
eq13 |> println

   r2^2 - (r1 + r2)^2 + (-r1 + 2*r1*(a^2 - a*r2 - r1*r2)/(a^2 - r1^2) - r2)^2

ans_r2 = solve(eq13, r2)[1]  # 1 of 2
ans_r2 |> println

   2*r1*(a^2 - a*r1 - a*sqrt(a^2 + r1^2) + r1^2 + r1*sqrt(a^2 + r1^2))/(a^2 + 2*a*r1 + r1^2)

小円の直径は，大円の直径と下底の関数として得られる。

r1 = 14/2, a = (18 +2/3)/2 を代入して 2 倍すれば，小円の直径 32/7 = 4 + 4/7 が得られる。

2ans_r2(r1 => 14/2, a => (18 + 2/3)/2) |> x -> rationalize(float(x), tol=1e-3)

   32//7

大円の直径が 14，下底が 18.6667(56/3) のとき，小円の直径は 4.57143(32/7) である。
上底は 8, 高さは 18.2857(128/7) である。

str(x) = replace(string(rationalize(x, tol=1e-3)), "//" => "/")

function draw(r1, a, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 2r1*(a^2 - a*r1 - a*sqrt(a^2 + r1^2) + r1^2 + r1*sqrt(a^2 + r1^2))/(a^2 + 2a*r1 + r1^2)
   (h, b) = (2r1*(a^2 - a*r2 - r1*r2)/(a^2 - r1^2), r2*(a + r1)/a)
   str1 = str(2a)
   str2 = str(2r2)
   str3 = str(h)
   @printf("大円の直径が %g，下底が %g(%s) のとき，小円の直径は %g(%s) である。\n上底は %g, 高さは %g(%s) である。\n", 2r1, 2a, str1, 2r2, str2, 2b, h, str3)
   println()
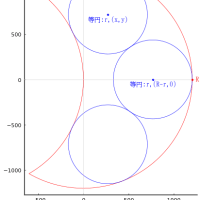
   plot([a, b, -b, -a, a], [0, h, h, 0, 0], color=:blue, lw=0.5)
   circle2(r2, h - r2, r2)
   circle(0, r1, r1, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, "a", :blue, :left, :bottom, delta=delta/2)
       point(b, h, "(b,h)", :blue, :left, :bottom, delta=delta/2)
       point(0, r1, "大円:r1,(0,r1)", :green, :center, delta=-delta/2)
       point(r2, h - r2, "小円:r2\n(r2,h-r2)", :red, :center, delta=-delta/2)
   end  
end;

draw(14/2, (18 + 2/3)/2, true)