算額(その1501)
五十八 岩手県花泉町 花泉天満宮 明治3年(1870)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市.
http://www.wasan.jp/yamamura/yamamura.html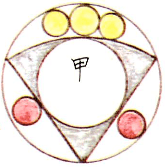
今有如図 03056
https://w.atwiki.jp/sangaku/pages/167.html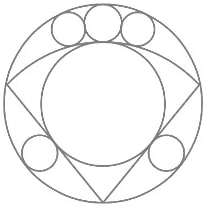
キーワード:円7個,外円,円弧,弦2本
#Julia, #SymPy, #算額, #和算
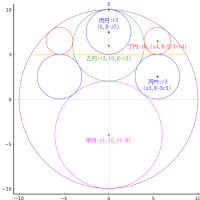
外円の中に扇形を容れ,甲円 1 個,乙円 3 個,丙円 2 個を容れる。甲円の直径が 41 寸のとき,丙円の直径はいかほどか。
これも,山村の図は明らかにおかしい。接すべきものが接していないのは手描きのずなのでやむを得ないかもしれないが,扇型の上にある黄色の 3 個の円は同じ乙円ではない。中央にある円と左右の円の大きさは普通に考えれば同じではない。同じだとすれば真ん中の円が外円と扇形に接するならば,左右の円は外円と扇形に同時に接することはできない。
ということで,この算額図も「今有如図」の方が正しい。黄色の真ん中の円と下の赤い 2 この円が乙円,左右の黄色の 2 個が丙円である。そのように仮定して求めた解は,答,術に一致する。
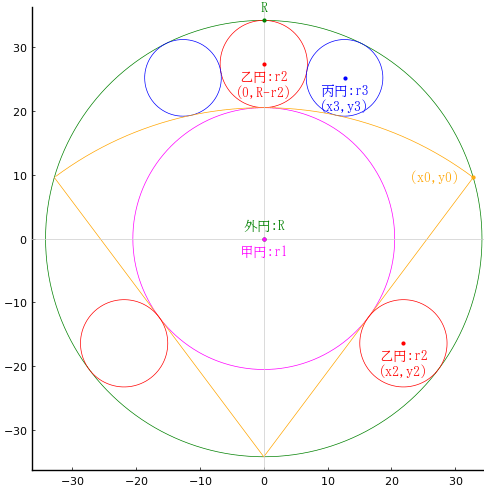
外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, 0); r1 = R - 2r2
乙円の半径と中心座標を r2, (0, R - r2), (x2, y2)
丙円の半径と中心座標を r3, (x3, y3)
扇型の半径と中心座標を (2R - 2r2), (0, -R)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms R::positive, r1::positive, r2::positive, r3::positive, x3::positive, y3::positive
R = r1 + 2r2
eq1 = x3^2 + y3^2 - (R - r3)^2
eq2 = x3^2 + (y3 + R)^2 - (r3 + (2R - 2r2))^2
eq3 = x3^2 + (R - r2 - y3)^2 - (r2 + r3)^2
eq4 = r1^2 + (R - r2)^2 - R^2
res = solve([eq1, eq2, eq3, eq4], (r2, r3, x3, y3))[1]
(r1/3, 12*r1/41, 8*sqrt(10)*r1/41, 151*r1/123)
丙円の半径 r3 は,甲円の半径 r1 の 12/41 倍である。
甲円の直径が 41 寸のとき,丙円の直径は 12 寸である。
算額の問に答えるのはここまでである。
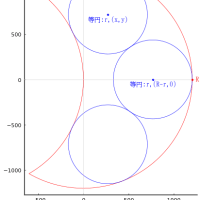
以下では,図を描くためのパラメータを求める。
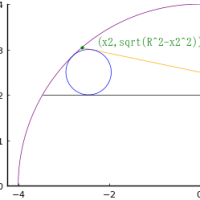
扇型と外円の交点座標を (x0, y0)
扇型の半径と外円に接する乙円の中心座標を (x2, y2)
として加え,8 元連立方程式を解く。
@syms x0, y0, x2, y2
eq5 = x0^2 + y0^2 - R^2
eq6 = x0^2 + (y0 + R)^2 - (2R - 2r2)^2
eq7 = dist2(0, -R, x0, y0, x2, y2, r3)
eq8 = x2^2 + y2^2 - (R - r2)^2
eq7 = y2/x2*(y0 + R)/x0 + 1;
res2 = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8], (r2, r3, x3, y3, x0, y0, x2, y2))
res2[4]
(r1/3, 12*r1/41, 8*sqrt(10)*r1/41, 151*r1/123, 8*r1/5, 7*r1/15, 16*r1/15, -4*r1/5)
甲円の直径が 41 のとき,全パラメータは以下のとおりである。
r2 = 6.83333; R = 34.1667; r1 = 20.5; r3 = 6; x3 = 12.6491; y3 = 25.1667; x2 = 21.8667; y2 = -16.4
function draw(r1, more=false)
pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r2, r3, x3, y3, x0, y0, x2, y2) = (r1/3, 12*r1/41, 8*sqrt(10)*r1/41, 151*r1/123, 8*r1/5, 7*r1/15, 16*r1/15, -4*r1/5)
R = r1 + 2r2
@printf("r2 = %g; R = %g; r1 = %g; r3 = %g; x3 = %g; y3 = %g; x2 = %g; y2 = %g\n", r2, R, r1, r3, x3, y3, x2, y2)
plot()
circle(0, 0, R, :green)
circle(0, R - r2, r2)
circle2(x3, y3, r3, :blue)
circle(0, 0, r1, :magenta)
θ = atand(y0 + R, x0)
circle(0, -R, 2R - 2r2, :orange, beginangle=θ, endangle=180 - θ)
plot!([-x0, 0, x0], [y0, -R, y0], color=:orange, lw=0.5)
circle2(x2, y2, r2, :red)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(0, 0, "外円:R", :green, :center, :bottom, delta=delta)
point(0, 0, "甲円:r1", :magenta, :center, delta=-delta)
point(0, R - r2, "乙円:r2\n(0,R-r2)", :red, :center, delta=-delta)
point(x2, y2, "乙円:r2\n(x2,y2)", :red, :center, delta=-delta)
point(x3, y3, "丙円:r3\n(x3,y3)", :blue, :center, delta=-delta)
point(0, R, "R", :green, :center, :bottom, delta=delta)
point(x0, y0, "(x0,y0) ", :orange, :right, :vcenter)
end
end;
draw(41/2, true)

























※コメント投稿者のブログIDはブログ作成者のみに通知されます