算額(その316)
(4) 京都府長岡京市天神 長岡天満宮 寛政2年(1970)
近畿数学史学会:近畿の算額「数学の絵馬を訪ねて」,平成4年5月16日 初版第一刷,大阪教育図書株式会社,大阪市.
森田健(2020): 日本文化としての数学:和算と算額, 日本語・日本文化,2020,47,p81-107.
https://ir.library.osaka-u.ac.jp/repo/ouka/all/75881/JLC_47_081.pdf
p02-03 特集「算額」(杉浦).indd
https://www.s-coop.net/lifestage/backnumber/2011/pdf/1106_02-03.pdf
キーワード:円2個,正三角形,直線上
大円と小円の間に正三角形が挟まっている。大円と小円の直径はそれぞれ 18cm,8cm である。正三角形の辺の長さを求めよ。
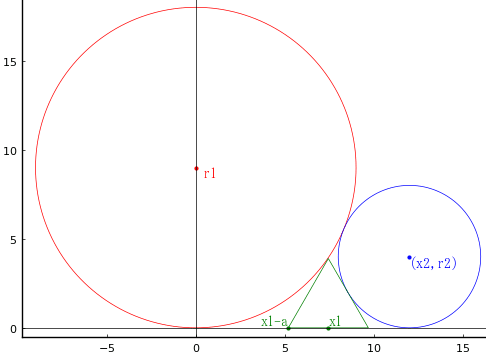
大円の半径を r1,中心座標を (0, r1)
小円の半径を r2,中心座標を (x2, r2)
正三角形の一辺の長さを 2a,底辺の中点の x 座標を x1 とする。
以下の連立方程式を解く。
なお,eq1 は直線の上にある外接する 2 つの円の中心間の距離を表すもので,距離 = x2 = 2sqrt(r1, r2) である。eq2, eq3 はそれれぞれの円の中心から正三角形の斜辺までの距離についての方程式である。
include("julia-source.txt");
using SymPy
@syms r1::positive, r2::positive, x2::positive, x1::positive, a::positive;
(r1, r2) = (9, 4)
eq1 = x2^2 + (r1 - r2)^2 - (r1 + r2)^2
eq2 = distance(x1 - a, 0, x1, sqrt(Sym(3))a, 0, r1) - r1^2
eq3 = distance(x1 + a, 0, x1, sqrt(Sym(3))a, x2, r2) - r2^2;
res = solve([eq1, eq2, eq3], (x1, a, x2))
3-element Vector{Tuple{Sym, Sym, Sym}}:
(6 - 5*sqrt(3)/2, 6 + 13*sqrt(3)/2, 12)
(6 + 7*sqrt(3)/2, sqrt(3)/2 + 6, 12)
(5*sqrt(3)/6 + 6, 6 - 13*sqrt(3)/6, 12)
三番目の組が適解である。
(5*sqrt(3)/6 + 6, 6 - 13*sqrt(3)/6, 12)
(7.4433756729740645, 2.247223250267433, 12)
正三角形の一辺の長さ = 4.494446500534866 cm
using Plots
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(r1, r2) = (9, 4)
x1 = 5*sqrt(3)/6 + 6
a = 6 - 13*sqrt(3)/6
x2 = 12
println("正三角形の一辺の長さ = $(2a) cm")
plot()
circle(0, r1, r1)
circle(x2, r2, r2, :blue)
plot!([x1 - a, x1 + a, x1, x1 - a], [0, 0, √3a, 0], color=:green, lw=0.5)
if more
point(0, r1, " r1", :red)
point(x2, r2, "(x2,r2)", :blue)
point(x1, 0, "x1", :green, :left, :bottom)
point(x1 - a, 0, "x1-a", :green, :right, :bottom)
vline!([0], color=:black, lw=0.5)
hline!([0], color=:black, lw=0.5)
else
plot!(showaxis=false)
end
end;


























※コメント投稿者のブログIDはブログ作成者のみに通知されます