算額（その1387）

算額（その1387）

七二 加須市大字外野 棘脱地蔵堂 明治7年(1874)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.
キーワード：円2個，直角三角形，正方形2個
#Julia, #SymPy, #算額, #和算

直角三角形の中に，正方形 2 個，日円，月円を容れる。月円の直径が 159 寸のとき，日円の直径はいかほどか。

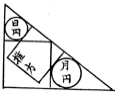
注1：この問題を解くにあたっては，鈎：股の比の情報が必要である。それが与えられれば，日円と月円を含む直角三角形の相似比が決まり，日円と月円の相似比も同じなので，日円の直径も簡単に！決まる。

注2：推方（傾いた正方形？）は意味のない情報である。なので，求めもしないし，図にも描かない。

鈎，股をそのまま変数名「鈎」，「股」
正方形の一辺の長さを a
日円の半径と中心座標を r1, (r1, a + r1)
月円の半径と中心座標を r2, (a + r2, r2)
とおき，以下の連立方程式を「月円を定数として」解く。

術は「月円の直径を三倍して四で割る」と，身も蓋もないことをいっている。
つまり，日円を含む直角三角形と月園を含む直角三角形の相似比，ひいては元の直角三角形の鈎と股の比が 3:4 であることを前提としている。上の図も 3:4 のときのものである。相似比が違えば，見かけの異なる図になる。

この時代（?）は，鈎股弦（直角三角形）といえば辺の比が 3:4:5 であるものと，暗黙の前提としていたのであろう。

ということで，eq2 は 鈎/股 = 3/4 を表している。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms 鈎::positive, 股::positive, a::positive,
     r1::positive, r2::positive
eq1 = (鈎 - a)/a - 鈎/股
eq2 = 鈎/股 - 3//4
eq5 = r1/r2 - a/(股 - a)
eq6 = sqrt((鈎 - a)^2 + a^2) + sqrt(a^2 + (股 - a)^2) - sqrt(鈎^2 + 股^2)
eq3 = (鈎 - a) + a - sqrt((鈎 - a)^2 + a^2) - 2r1
eq4 = a + (股 - a) - sqrt(a^2 + (股 - a)^2) - 2r2;

得られる解は非常にきれいな結果である。

日円の半径 r1 は，月円の半径 r2 の 3/4 倍である。

res = solve([eq2, eq3, eq4, eq5], (鈎, 股, a, r1))[1]

   (21*r2/4, 7*r2, 3*r2, 3*r2/4)

その結果，「月円の直径が 159 寸」のとき，「日円の直径は 159*3/4 = 119.25 寸」が得られる。

一般的に，算額の問は「きれいな数の答えが得られる」ように設定されることが多い。

もし，問が「月円の直径が 160 寸」ならば，「日円の直径は 160*3/4 = 120 寸」が得られるのになぜそうしなかったのか。

鈎股弦の比が 3:4:5 というのを隠そうとしたのか。

人心を惑わす，問題に無関係な推方（傾いた正方形？）を持ち出した理由も含め，謎は尽きない。

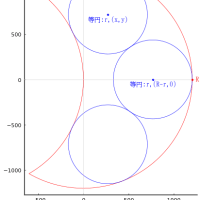
function draw(r2, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股, a, r1) = (21*r2/4, 7*r2, 3*r2, 3*r2/4)
   @printf("月円の直径が %g のとき，日円の直径は %g である。\n",  2r2, 2r1)
   @printf("r2 = %g;  鈎 = %g;  股 = %g;  a = %g;  r1 = %g\n", r2, 鈎, 股, a, r1)
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:green, lw=0.5)
   rect(0, 0, a, a, :blue)
   circle(r1, a + r1, r1)
   circle(a + r2, r2, r2, :magenta)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 鈎, "鈎 ", :green, :right, :vcenter)
       point(股, 0, "股", :green, :center, delta=-delta)
       point(a, a, "(a,a)", :blue, :left, :bottom, delta=delta)
       point(r1, a + r1, "日円:r1\n(r1,a+r1)", :red, :center, delta=-delta)
       point(a + r2, r2, "月円:r2\n(a+r2,r2)", :magenta, :center, delta=-delta)
       plot!(xlims=(-6delta, 股 + 5delta), ylims=(-6delta, 鈎 + 5delta))
   end
end;

draw(159/2, true)