算額（その237）

算額（その237）

七四 加須市大字外野 棘脱地蔵堂 明治7年(1874)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

山形県南原町 熊野神社
山形算額勝負-湯殿山神社を目指せ-
https://www.sci.yamagata-u.ac.jp/wasan/pdf/20180711SSEP.pdf

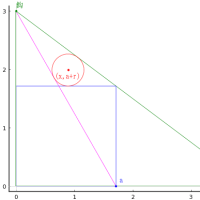
外円内に大円 2 個，小円 2 個が入っている。大円の径が 3寸のとき，小円の径はいかほどか。

算額の図では左右対称に見えないが，条件からすると左右対称でしかありえない。 すなわち，外円の中心を原点に置くと，小円の中心は x 座標軸上，大円の中心は y 座標軸上にあるべき。

外円の中心を原点(0, 0) におき，半径を r0 とする。 大円の半径を r1 とし，中心座標を (0, r1) に置く。r1 = r0/2 である。 小円の半径を r2 とし，中心座標を (r0 - r2, 0) とする。 以下の方程式を解く。

include("julia-source.txt")

using SymPy

@syms r0, r1, r2
r1 = 3//2
eq0 = r1 - r0//2
eq1 = (r0 - r2)^2 + r1^2 - (r1 + r2)^2
solve([eq0, eq1], (r0, r2))

   1-element Vector{Tuple{Sym, Sym}}:
    (3, 1)

外円の直径は 6 寸，小円の直径は 2 寸である。

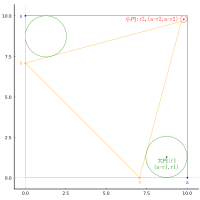
function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r0, r2) = (3, 1)
   @printf("小円の直径 = %.7f\n", 2r2)
   plot()
   circle(0, 0, r0, :black)
   circle(0, r1, r1, :green)
   circle(0, -r1, r1, :green)
   circle(r0 - r2, 0, r2)
   circle(-r0 + r2, 0, r2)
   if more == true
       point(0, r1, " r1")
       point(r1/2, 1.2r1, "大円", mark=false)
       point(r0 - r2, 0, " r0-r2", :red)
       point(r0 - r2, 0.5r2, "小円", :red, mark=false)
       hline!([0], color=:black, lw=0.5)
       vline!([0], color=:black, lw=0.5)
   else
       plot!(showaxis=false)
   end
end;