算額（その1400）

算額（その1400）

十八 岩手県平泉町 弁慶堂（現在は地蔵堂にて保管） 安政6年(1859)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html
キーワード：円7個，楕円個，正方形
#Julia, #SymPy, #算額, #和算

正方形の中に，等円 4 個，甲円，乙円，楕円，を容れる。正方形の一辺の長さが 1 寸のとき，乙円の直径はいかほどか。

注：乙円は楕円と外接しているが，等円には接していない。楕円の中の等円を見れば，等円は曲率円であることがわかる。元図には乙円は2個しか描かれていないが，図形は上下対称なので，式を書く便宜上 4 個描くことにする。

正方形の一辺の長さを 2a
楕円の長半径，短半径，中心座標は a, r1, (0, 0)
甲円の半径と中心座標を r1, (0, 0)
乙円の半径と中心座標を r2, (a - r2, a - r2)
等円の半径と中心座標を r3, (0, a - r3)
楕円と乙円の接点の座標を (x0, y0)
とおき，以下の連立方程式を解く。

甲円と丙円の直径は eq1, eq2 を連立方程式として簡単に求めることができる。
甲円と丙円の直径は正方形の一辺の長さの 1/2，1/4 である。
正方形の一辺の長さが 1 寸のとき，甲円と丙円の直径は 0.5 寸，0.25 寸である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

@syms a, r1, r3
b = r1
eq1 = r3 - b^2/a
eq2 = r1 + 2r3 - a
solve([eq1, eq2], (r1, r3))[2]  # 2 of 2

   (a/2, a/4)

乙円は甲円の直径がわかれば（丙円の直径には無関係），楕円と乙円の接点座標 (x0, y0) とともに eq3, eq4, eq5 の三元連立方程式を立てることで解が得られるが，SymPy の能力的に一度に解を求めることが難しい。また，正方形の一辺の長さを 1 としても一般性を失わないので， a = 1/2, r1 = a/2 として，逐次的に r2, x0, y0 を求める。

using SymPy
@syms a, r1, r2, r3, x0, y0
a = 1//2
r1 = a//2
b = r1
eq3 = x0^2/a^2 + y0^2/b^2 - 1
eq4 = -b^2*x0/(a^2*y0) + (a - r2 - x0)/(a - r2 - y0)
eq5 = (x0 - a + r2)^2 + (y0 - a + r2)^2 - r2^2;

まず，eq3 を解いて x0 を求める。

ans_x0 = solve(eq3, x0)[2]
ans_x0 |> println

   sqrt(1 - 16*y0^2)/2

eq4 の x に代入し，r2 を求める。

eq14 = eq4(x0 => ans_x0) |> simplify |> numerator
ans_r2 = solve(eq14, r2)[1] |> simplify
ans_r2 |> println

   (-6*y0*sqrt(1 - 16*y0^2) + 8*y0 - sqrt(1 - 16*y0^2))/(2*(8*y0 - sqrt(1 - 16*y0^2)))

eq5 の x0, r2 に代入し，y0 を求める。

eq15 = eq5(x0 => ans_x0, r2 => ans_r2) |> simplify |> numerator
ans_y0 = solve(eq15, y0);

eq15 は 5次式 f(x) = 512*x^5 - 512*x^4 + 64*x^3 + 48*x^2 - 4*x - 1 のときの，f(x) = 0 の実数解であり，3 番目のものが適解である。

@syms x
pyplot(size=(300, 200), grid=false, aspectratio=:none, label="")
plot(512*x^5 - 512*x^4 + 64*x^3 + 48*x^2 - 4*x - 1, xlabel="x", ylabel="f(x)", xlims=(-0.3, 0.7))
hline!([0])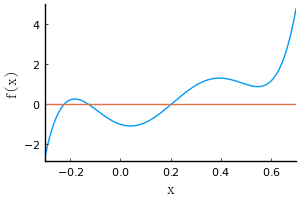

ans_y0[3] |> println

   CRootOf(512*x^5 - 512*x^4 + 64*x^3 + 48*x^2 - 4*x - 1, 2)

数値としては 0.202203526591889 である。

ans_y0[3].evalf() |> println

   0.202203526591889

y0 の実際の値が求まれば，r2, x0 の実際の値も求まる。

y0 = 0.202203526591889 のとき，ans_r2 の式に代入することにより，r2 = 0.15351726189219103 である。

y0 = 0.202203526591889
(-6*y0*sqrt(1 - 16*y0^2) + 8*y0 - sqrt(1 - 16*y0^2))/(2*(8*y0 - sqrt(1 - 16*y0^2)))

   0.15351726189219103

さらに，y0, r2 を ans_x0 の式に代入することにより，x0 = 0.29403220118757906 を得る。

y0 = 0.202203526591889
r2 = 0.15351726189219103
sqrt(1 - 16*y0^2)/2

   0.29403220118757906

正方形の一辺の長さが 1 のとき，
乙円の直径は 2*0.15351726189219103 = 0.30703452378438206
接点の座標は (0.29403220118757906, 0.202203526591889)
である。

乙円の直径は 0.30703452378438206 寸である。

「答」では「3分7厘」としているが，単なる書き間違いである。以下に示すように「術」のとおりに計算すれば，0.307034523784383 が得られる。

なお，山村は術を『答と合わせるため「内減乙径再乗巾二十七段」とある所を「内減乙径再乗巾二百三十三段」と訂正して計算することにする』としているが，これは不適切にもほどがある。山村の計算が間違いである。途中の数式の展開において誤りが多く，最後の「式」も当然ながら正しくない。自らの間違いを棚に上げて術を訂正する，しかもその訂正の根拠すら正しくないというのは，もってのほかである。

元のままで正しい答えが出る。術は以下のように計算している。

@syms 方面, x
天 = 方面 - x
# 山村は，27 倍するところを勝手に 233 倍した
# 左寄 = ((天*方面*3 + x^2)*天*61 - x^3*233)*方面^2 
# 術における以下の式は正しい
左寄 = ((天*方面*3 + x^2)*天*61 - x^3*27)*方面^2
左寄 = 左寄(方面 => 1) |> expand
左寄 |> println

   -88*x^3 + 244*x^2 - 366*x + 183

相消 = ((天 + 方面)*2)^4 * 天
相消 = 相消(方面 => 1) |> expand
相消 |> println

   -16*x^5 + 144*x^4 - 512*x^3 + 896*x^2 - 768*x + 256

式 = 左寄 - 相消
式 |> println

   16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73

x についての 5 次式の解を求める。

res = solve(式, x)
res[1] |> println
res[2] |> println
res[3] |> println
res[4] |> println
res[5] |> println

   CRootOf(16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73, 0)
   CRootOf(16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73, 1)
   CRootOf(16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73, 2)
   CRootOf(16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73, 3)
   CRootOf(16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73, 4)

最初のものが実数解である。ほかは全て虚数解で不適切。

乙円の直径は x = 0.307034523784383 である。
「答」の 「三分七厘 0.37」 は 「三分零厘七毛 0.307」の書き間違いである。

x = 0.307 ならば，式 = 0 となるべきところが，誤差は -0.00364534705107467であり，
x = 0.37 ならば，式 = 0 となるべきところが，誤差は 5.37023049119999 となる。
算額の作者も山村も，検算をすれば誤りを見つけることができたのに，残念なことだ。

結論：「術は正しい。答えは書き間違い。山村の解説は不適切である。」
だいじなことなので，何度でも書きます。

res[1] |> println
res[1].evalf() |> println
式(x => 0.307) |> println
式(x => 0.37) |> println

   CRootOf(16*x^5 - 144*x^4 + 424*x^3 - 652*x^2 + 402*x - 73, 0)
   0.307034523784383
   -0.00364534705107467
   5.37023049119999

function draw(a, more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho") 
   (r1, r2, r3, x0, y0) = [0.25, 0.15351726189219161, 0.125, 0.2940322011875788, 0.2022035265918891]
   b = r1
   @printf("a = %g;  b = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x0 = %g;  y0 = %g\n", a, b, r1, r2, r3, x0, y0)
   plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:green, lw=0.5)
   ellipse(0, 0, a, b, color=:blue)
   circle4(a - r2, a - r2, r2)
   circle(0, 0, r1, :magenta)
   circle42(0, a - r3, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       #point(x0, y0)
   end  
end;

draw(1/2, true)