算額(その34)
三重県四日市市 川島神明神社 天保15年
http://www.wasan.jp/mie/sinmei1.html
直径121寸8分の大円と直線に接する円,およびこの円と大円に接する小さな円がある。小さな円の直径が1分になるのは何番目の円か。
以下のプログラムでは半径1218分の円と考える。求めるのは小円の半径が1分の円である。
答えを最初に書いておく。
16 番目の小円の半径が 0.9918566461328249 である。
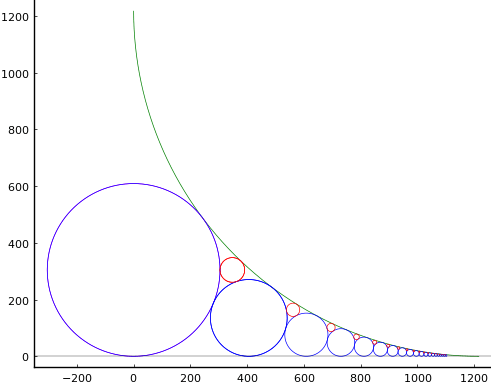
まず大円と直線に接する円の直径と中心の x 座標の漸化式を求める。
using SymPy
@syms xi, xi1, ri, ri1, R;
eq1 = (xi1 - xi)^2 + (ri - ri1)^2 - (ri + ri1)^2
eq2 = (R - xi)^2 + (R - ri)^2 - (R + ri)^2
eq3 = (R - xi1)^2 + (R - ri1)^2 - (R + ri1)^2;
res = solve([eq1, eq2, eq3], (xi1, ri1))
2-element Vector{Tuple{Sym, Sym}}:
((R^2 - xi^2 + (-4*R + 4*ri)*(-sqrt(R*ri)*(R - xi)^2/(2*(R^2 - 2*R*ri + ri^2)) + (R + ri)*(R - xi)^2/(4*(R - ri)^2)))/(2*(R - xi)), -sqrt(R*ri)*(R - xi)^2/(2*(R^2 - 2*R*ri + ri^2)) + (R + ri)*(R - xi)^2/(4*(R - ri)^2))
((R^2 - xi^2 + (-4*R + 4*ri)*(sqrt(R*ri)*(R - xi)^2/(2*(R^2 - 2*R*ri + ri^2)) + (R + ri)*(R - xi)^2/(4*(R - ri)^2)))/(2*(R - xi)), sqrt(R*ri)*(R - xi)^2/(2*(R^2 - 2*R*ri + ri^2)) + (R + ri)*(R - xi)^2/(4*(R - ri)^2))
res[2] は不適切解である。
function f(x, r; R=1218) # 次の円のx座標と半径
return (-R*r + R*x + R*sqrt(R*r) - x*sqrt(R*r))/(R - r), (R - x)^2*(R + r - 2*sqrt(R*r))/(4*(R - r)^2)
end;
function nextcircle(n) # 後で使うために配列に収める
xa = zeros(n)
ra = zeros(n)
x = 0
r = 609/2
xa[1] = x
ra[1] = r
for i = 2:n
x, r = f(x, r)
#println("$i: x = $x, r = $r")
xa[i] = x
ra[i] = r
end
return xa, ra
end;
次に,大円と前述の円に接する小円の半径と中心座標を求める漸化式を作る。
using SymPy
@syms R::positive, r1::positive, r2::positive, r3::positive, x2::positive, x3::positive, y3::positive;
@syms X2::positive, Y2::positive, ra2::positive;
eq1 = (R - x2)^2 + (R - r2)^2 - (R + r2)^2
eq2 = (x3 - x2)^2 + (r2 - r3)^2 - (r2 + r3)^2
eq3 = (R - x3)^2 + (R - r3)^2 - (R + r3)^2
eq4 = (X2 - x2)^2 + (Y2 - r2)^2 - (ra2 + r2)^2
eq5 = (x3 - X2)^2 + (Y2 - r3)^2 - (ra2 + r3)^2
eq6 = (R - X2)^2 + (R - Y2)^2 - (R + ra2)^2;
res = solve([eq1, eq2, eq3, eq4, eq5, eq6], (X2, Y2, ra2))
1-element Vector{Tuple{Sym, Sym, Sym}}:
((R^2*r2 - R^2*r3 - R*x2^2 + R*x3^2 - r2*x3^2 + r3*x2^2)/(2*(R*r2 - R*r3 - R*x2 + R*x3 - r2*x3 + r3*x2)), -(-R^4*r2^2 + 2*R^4*r2*r3 - R^4*r3^2 + R^4*x2^2 - 2*R^4*x2*x3 + R^4*x3^2 + 4*R^3*r2^2*x3 - 4*R^3*r2*r3*x2 - 4*R^3*r2*r3*x3 + 2*R^3*r2*x2^2 - 4*R^3*r2*x2*x3 + 2*R^3*r2*x3^2 + 4*R^3*r3^2*x2 + 2*R^3*r3*x2^2 - 4*R^3*r3*x2*x3 + 2*R^3*r3*x3^2 - 2*R^3*x2^3 + 2*R^3*x2^2*x3 + 2*R^3*x2*x3^2 - 2*R^3*x3^3 - 6*R^2*r2^2*x3^2 + 2*R^2*r2*r3*x2^2 + 8*R^2*r2*r3*x2*x3 + 2*R^2*r2*r3*x3^2 - 4*R^2*r2*x2^2*x3 + 8*R^2*r2*x2*x3^2 - 4*R^2*r2*x3^3 - 6*R^2*r3^2*x2^2 - 4*R^2*r3*x2^3 + 8*R^2*r3*x2^2*x3 - 4*R^2*r3*x2*x3^2 + 6*R^2*x2^3*x3 - 12*R^2*x2^2*x3^2 + 6*R^2*x2*x3^3 + 4*R*r2^2*x3^3 - 4*R*r2*r3*x2^2*x3 - 4*R*r2*r3*x2*x3^2 + 2*R*r2*x2^2*x3^2 - 4*R*r2*x2*x3^3 + 2*R*r2*x3^4 + 4*R*r3^2*x2^3 + 2*R*r3*x2^4 - 4*R*r3*x2^3*x3 + 2*R*r3*x2^2*x3^2 - 2*R*x2^4*x3 + 2*R*x2^3*x3^2 + 2*R*x2^2*x3^3 - 2*R*x2*x3^4 - r2^2*x3^4 + 2*r2*r3*x2^2*x3^2 - r3^2*x2^4 + x2^4*x3^2 - 2*x2^3*x3^3 + x2^2*x3^4)/(4*(-R + x2)*(-R + x3)*(x2 - x3)*(R*r2 - R*r3 - R*x2 + R*x3 - r2*x3 + r3*x2)), -(R^4*r2^2 - 2*R^4*r2*r3 + R^4*r3^2 + R^4*x2^2 - 2*R^4*x2*x3 + R^4*x3^2 - 4*R^3*r2^2*x3 + 4*R^3*r2*r3*x2 + 4*R^3*r2*r3*x3 - 2*R^3*r2*x2^2 + 4*R^3*r2*x2*x3 - 2*R^3*r2*x3^2 - 4*R^3*r3^2*x2 - 2*R^3*r3*x2^2 + 4*R^3*r3*x2*x3 - 2*R^3*r3*x3^2 - 2*R^3*x2^3 + 2*R^3*x2^2*x3 + 2*R^3*x2*x3^2 - 2*R^3*x3^3 + 6*R^2*r2^2*x3^2 - 2*R^2*r2*r3*x2^2 - 8*R^2*r2*r3*x2*x3 - 2*R^2*r2*r3*x3^2 + 4*R^2*r2*x2^2*x3 - 8*R^2*r2*x2*x3^2 + 4*R^2*r2*x3^3 + 6*R^2*r3^2*x2^2 + 4*R^2*r3*x2^3 - 8*R^2*r3*x2^2*x3 + 4*R^2*r3*x2*x3^2 + 2*R^2*x2^4 - 2*R^2*x2^3*x3 - 2*R^2*x2*x3^3 + 2*R^2*x3^4 - 4*R*r2^2*x3^3 + 4*R*r2*r3*x2^2*x3 + 4*R*r2*r3*x2*x3^2 - 2*R*r2*x2^2*x3^2 + 4*R*r2*x2*x3^3 - 2*R*r2*x3^4 - 4*R*r3^2*x2^3 - 2*R*r3*x2^4 + 4*R*r3*x2^3*x3 - 2*R*r3*x2^2*x3^2 - 2*R*x2^4*x3 + 2*R*x2^3*x3^2 + 2*R*x2^2*x3^3 - 2*R*x2*x3^4 + r2^2*x3^4 - 2*r2*r3*x2^2*x3^2 + r3^2*x2^4 + x2^4*x3^2 - 2*x2^3*x3^3 + x2^2*x3^4)/(4*(-R + x2)*(-R + x3)*(x2 - x3)*(R*r2 - R*r3 - R*x2 + R*x3 - r2*x3 + r3*x2)))
次の小円を求める関数を定義する。
function nextcircle2(x, r, i; R=1218)
X = (R^2*r[i] - R^2*r[i+1] - R*x[i]^2 + R*x[i+1]^2 - r[i]*x[i+1]^2 + r[i+1]*x[i]^2)/(2*(R*r[i] - R*r[i+1] - R*x[i] + R*x[i+1] - r[i]*x[i+1] + r[i+1]*x[i]))
Y = (R^4*r[i]^2/4 - R^4*r[i]*r[i+1]/2 + R^4*r[i+1]^2/4 - R^4*x[i]^2/4 + R^4*x[i]*x[i+1]/2 - R^4*x[i+1]^2/4 - R^3*r[i]^2*x[i+1] + R^3*r[i]*r[i+1]*x[i] + R^3*r[i]*r[i+1]*x[i+1] - R^3*r[i]*x[i]^2/2 + R^3*r[i]*x[i]*x[i+1] - R^3*r[i]*x[i+1]^2/2 - R^3*r[i+1]^2*x[i] - R^3*r[i+1]*x[i]^2/2 + R^3*r[i+1]*x[i]*x[i+1] - R^3*r[i+1]*x[i+1]^2/2 + R^3*x[i]^3/2 - R^3*x[i]^2*x[i+1]/2 - R^3*x[i]*x[i+1]^2/2 + R^3*x[i+1]^3/2 + 3*R^2*r[i]^2*x[i+1]^2/2 - R^2*r[i]*r[i+1]*x[i]^2/2 - 2*R^2*r[i]*r[i+1]*x[i]*x[i+1] - R^2*r[i]*r[i+1]*x[i+1]^2/2 + R^2*r[i]*x[i]^2*x[i+1] - 2*R^2*r[i]*x[i]*x[i+1]^2 + R^2*r[i]*x[i+1]^3 + 3*R^2*r[i+1]^2*x[i]^2/2 + R^2*r[i+1]*x[i]^3 - 2*R^2*r[i+1]*x[i]^2*x[i+1] + R^2*r[i+1]*x[i]*x[i+1]^2 - 3*R^2*x[i]^3*x[i+1]/2 + 3*R^2*x[i]^2*x[i+1]^2 - 3*R^2*x[i]*x[i+1]^3/2 - R*r[i]^2*x[i+1]^3 + R*r[i]*r[i+1]*x[i]^2*x[i+1] + R*r[i]*r[i+1]*x[i]*x[i+1]^2 - R*r[i]*x[i]^2*x[i+1]^2/2 + R*r[i]*x[i]*x[i+1]^3 - R*r[i]*x[i+1]^4/2 - R*r[i+1]^2*x[i]^3 - R*r[i+1]*x[i]^4/2 + R*r[i+1]*x[i]^3*x[i+1] - R*r[i+1]*x[i]^2*x[i+1]^2/2 + R*x[i]^4*x[i+1]/2 - R*x[i]^3*x[i+1]^2/2 - R*x[i]^2*x[i+1]^3/2 + R*x[i]*x[i+1]^4/2 + r[i]^2*x[i+1]^4/4 - r[i]*r[i+1]*x[i]^2*x[i+1]^2/2 + r[i+1]^2*x[i]^4/4 - x[i]^4*x[i+1]^2/4 + x[i]^3*x[i+1]^3/2 - x[i]^2*x[i+1]^4/4)/((R - x[i])*(R - x[i+1])*(x[i] - x[i+1])*(R*r[i] - R*r[i+1] - R*x[i] + R*x[i+1] - r[i]*x[i+1] + r[i+1]*x[i]))
rr = (-R^4*r[i]^2/4 + R^4*r[i]*r[i+1]/2 - R^4*r[i+1]^2/4 - R^4*x[i]^2/4 + R^4*x[i]*x[i+1]/2 - R^4*x[i+1]^2/4 + R^3*r[i]^2*x[i+1] - R^3*r[i]*r[i+1]*x[i] - R^3*r[i]*r[i+1]*x[i+1] + R^3*r[i]*x[i]^2/2 - R^3*r[i]*x[i]*x[i+1] + R^3*r[i]*x[i+1]^2/2 + R^3*r[i+1]^2*x[i] + R^3*r[i+1]*x[i]^2/2 - R^3*r[i+1]*x[i]*x[i+1] + R^3*r[i+1]*x[i+1]^2/2 + R^3*x[i]^3/2 - R^3*x[i]^2*x[i+1]/2 - R^3*x[i]*x[i+1]^2/2 + R^3*x[i+1]^3/2 - 3*R^2*r[i]^2*x[i+1]^2/2 + R^2*r[i]*r[i+1]*x[i]^2/2 + 2*R^2*r[i]*r[i+1]*x[i]*x[i+1] + R^2*r[i]*r[i+1]*x[i+1]^2/2 - R^2*r[i]*x[i]^2*x[i+1] + 2*R^2*r[i]*x[i]*x[i+1]^2 - R^2*r[i]*x[i+1]^3 - 3*R^2*r[i+1]^2*x[i]^2/2 - R^2*r[i+1]*x[i]^3 + 2*R^2*r[i+1]*x[i]^2*x[i+1] - R^2*r[i+1]*x[i]*x[i+1]^2 - R^2*x[i]^4/2 + R^2*x[i]^3*x[i+1]/2 + R^2*x[i]*x[i+1]^3/2 - R^2*x[i+1]^4/2 + R*r[i]^2*x[i+1]^3 - R*r[i]*r[i+1]*x[i]^2*x[i+1] - R*r[i]*r[i+1]*x[i]*x[i+1]^2 + R*r[i]*x[i]^2*x[i+1]^2/2 - R*r[i]*x[i]*x[i+1]^3 + R*r[i]*x[i+1]^4/2 + R*r[i+1]^2*x[i]^3 + R*r[i+1]*x[i]^4/2 - R*r[i+1]*x[i]^3*x[i+1] + R*r[i+1]*x[i]^2*x[i+1]^2/2 + R*x[i]^4*x[i+1]/2 - R*x[i]^3*x[i+1]^2/2 - R*x[i]^2*x[i+1]^3/2 + R*x[i]*x[i+1]^4/2 - r[i]^2*x[i+1]^4/4 + r[i]*r[i+1]*x[i]^2*x[i+1]^2/2 - r[i+1]^2*x[i]^4/4 - x[i]^4*x[i+1]^2/4 + x[i]^3*x[i+1]^3/2 - x[i]^2*x[i+1]^4/4)/((R - x[i])*(R - x[i+1])*(x[i] - x[i+1])*(R*r[i] - R*r[i+1] - R*x[i] + R*x[i+1] - r[i]*x[i+1] + r[i+1]*x[i]))
return X, Y, rr
end;
using Plots
function circle(ox, oy, r, color=:red; beginangle=0, endangle=360)
θ = beginangle:0.1:endangle
x = r.*cosd.(θ)
y = r.*sind.(θ)
plot!(ox .+ x, oy .+ y, color=color, linewidth=0.5)
end;
function point(x, y, string="", color=:green, position=:left, vertical=:top)
scatter!([x], [y], color=color, markerstrokewidth=0)
annotate!(x, y, text(string, 10, position, color, vertical))
end;
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
R = 1218
(r1, r2, r3, x2, x3, y3) = (609/2, 406/3, 87/2, 406, 348, 609/2)
println("r1 = $r1; r2 = $r2; r3 = $r3")
println("x2= $x2; x3 = $x3; y3 = $y3")
plot()
circle(R, R, R, :green, beginangle=180, endangle=270)
circle(0, r1, r1, :magenta)
circle(x2, r2, r2, :blue)
circle(x3, y3, r3, :red)
xa, ra = nextcircle(20)
println("デカルトの円定理から,小円の半径のみを求める")
kR = 1/R
ka = 1 ./ ra
for i = 1:19
k4 = kR + ka[i] + ka[i+1] + 2sqrt(kR*ka[i] + ka[i]*ka[i+1] + ka[i+1]*kR)
r = 1/k4
println("$i, $r")
end
for i = 1:20
circle(xa[i], ra[i], ra[i], :blue)
end
println("小円の半径,中心座標を求める")
for i = 1:19
X, Y, rr = nextcircle2(xa, ra, i)
circle(X, Y, rr)
println("i = $i, x = $X, y = $Y, r = $rr")
end
hline!([0], color=:black, linewidth=0.25)
end;
draw(false)
r1 = 304.5; r2 = 135.33333333333334; r3 = 43.5
x2= 406; x3 = 348; y3 = 304.5
デカルトの円定理から,小円の半径のみを求める
1, 43.5
2, 23.423076923076916
3, 14.499999999999996
4, 9.822580645161292
5, 7.0813953488372094
6, 5.342105263157894
7, 4.171232876712329
8, 3.3461538461538454
9, 2.7432432432432425
10, 2.2894736842105234
11, 1.9394904458598707
12, 1.663934426229509
13, 1.4431279620853108
14, 1.2634854771784254
15, 1.1153846153846176
16, 0.9918566775244327
17, 0.8877551020408169
18, 0.7992125984251943
19, 0.7232779097387141
小円の半径,中心座標を求める
i = 1, x = 348.0, y = 304.49999999999994, r = 43.499999999999986
i = 2, x = 562.1538461538463, y = 163.96153846153766, r = 23.423076923075435
i = 3, x = 695.9999999999999, y = 101.50000000001576, r = 14.499999999987837
i = 4, x = 785.8064516129033, y = 68.75806451612152, r = 9.82258064507806
i = 5, x = 849.7674418604653, y = 49.56976744177949, r = 7.08139534902618
i = 6, x = 897.4736842105261, y = 37.39473684132309, r = 5.342105263101324
i = 7, x = 934.3561643835608, y = 29.198630137693904, r = 4.171232877205791
i = 8, x = 963.6923076923063, y = 23.423076928931703, r = 3.346153845145927
i = 9, x = 987.5675675675733, y = 19.202702699235346, r = 2.7432432427479063
i = 10, x = 1007.3684210526319, y = 16.02631580210383, r = 2.2894736816354584
i = 11, x = 1024.0509554140167, y = 13.576433082760703, r = 1.9394904363737546
i = 12, x = 1038.2950819672076, y = 11.6475410215815, r = 1.663934370306387
i = 13, x = 1050.5971563981027, y = 10.101895600212682, r = 1.443127868224802
i = 14, x = 1061.3278008298776, y = 8.844398562571168, r = 1.2634854854616941
i = 15, x = 1070.7692307692128, y = 7.807692179665674, r = 1.1153844774220047
i = 16, x = 1079.140065146608, y = 6.942996352466482, r = 0.9918566461328249
i = 17, x = 1086.6122448979554, y = 6.214286399607383, r = 0.8877555400354336
i = 18, x = 1093.322834645682, y = 5.594488988858351, r = 0.7992131560152675
i = 19, x = 1099.3824228028282, y = 5.062945169849251, r = 0.7232791103597648
16 番目の小円の半径が 0.9918566461328249 である。


























※コメント投稿者のブログIDはブログ作成者のみに通知されます