算額（その1358）

算額（その1358）

十九 群馬県群馬郡榛名町榛名山 榛名神社 文化8年(1811)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円4個，長方形，斜線
#Julia, #SymPy, #算額, #和算

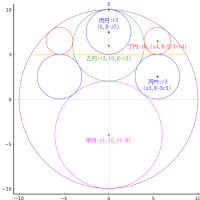
長方形の中に斜線を隔てて大円 1 個，中円 2 個，小円 1 個を容れる。大円の直径が 10 寸のとき，小円の直径はいかほどか。

長方形の短辺と長辺の長さを a, b
斜線と長方形の辺の交点座標を (c, 0), (a, d)
大円の半径と中心座標を r1, (r1, b - r1)
中円の半径と中心座標を r2, (r2, r2), (a - r2, r2)
小円の半径と中心座標を r3, (a - r3, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::positive, d::positive,
     r1::positive, r2::positive, r3::positive, y3::positive
eq1 = dist2(c, 0, a, d, r1, b - r1, r1)
eq2 = dist2(c, 0, a, d, r2, r2, r2)
eq3 = dist2(c, 0, a, d, a - r2, r2, r2)
eq4 = dist2(c, 0, a, d, a - r3, y3, r3)
eq5 = (r1 - r2)^2 + (b - r1 - r2)^2 - (r1 + r2)^2
eq6 = (r2 - r3)^2 + (y3 - r2)^2 - (r2 + r3)^2
eq7 = (a - c) + d - sqrt((a - c)^2 + d^2) - 2r2;
# eq8 = ((a - c) + d + sqrt((a - c)^2 + d^2))*r2 - (a - c)*d;
# res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7], (a, b, c, d, r2, r3, y3))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, b, c, d, r2, r3, y3) = u
   return [
       a^2*b^2 - 2*a^2*b*r1 - 2*a*b^2*c + 2*a*b*c*d + 4*a*b*c*r1 - 2*a*b*d*r1 - 2*a*c*d*r1 + 2*a*d*r1^2 + b^2*c^2 - 2*b*c^2*d - 2*b*c^2*r1 + 2*b*c*d*r1 + c^2*d^2 + 2*c^2*d*r1 - 2*c*d^2*r1 - 2*c*d*r1^2,  # eq1
       d*(2*a*c*r2 - 2*a*r2^2 + c^2*d - 2*c^2*r2 - 2*c*d*r2 + 2*c*r2^2),  # eq2
       d*(a^2*d - 2*a^2*r2 - 2*a*c*d + 4*a*c*r2 - 2*a*d*r2 + 2*a*r2^2 + c^2*d - 2*c^2*r2 + 2*c*d*r2 - 2*c*r2^2),  # eq3
       a^2*d^2 - 2*a^2*d*y3 - a^2*r3^2 + a^2*y3^2 - 2*a*c*d^2 + 4*a*c*d*y3 + 2*a*c*r3^2 - 2*a*c*y3^2 - 2*a*d^2*r3 + 2*a*d*r3*y3 + c^2*d^2 - 2*c^2*d*y3 - c^2*r3^2 + c^2*y3^2 + 2*c*d^2*r3 - 2*c*d*r3*y3,  # eq4
       (r1 - r2)^2 - (r1 + r2)^2 + (b - r1 - r2)^2,  # eq5
       (-r2 + y3)^2 + (r2 - r3)^2 - (r2 + r3)^2,  # eq6
       a - c + d - 2*r2 - sqrt(d^2 + (a - c)^2),  # eq7
   ]
end;
r1 = 10/2
#iniv = BigFloat[13.2, 16, 5, 16, 3, 2, 8]
iniv = BigFloat[12.2, 15.2, 4.3, 12.2, 2.8, 1.5, 6.9]
res = nls(H, ini=iniv)

   ([12.21558138691064, 15.247885379719106, 4.29489761141387, 12.16723318645839, 2.784847053174034, 1.5510746219144202, 6.941531111454818], true)

数値解は初期値の与え方で，見た目の図が変わる。

例えば，先に掲げた図は，以下のパラメータで描画したものである。

大円の直径が 10 のとき，小円の直径は 3.10215 である。中円の直径は 5.56969 である。
r1 = 5;  a = 12.2156;  b = 15.2479;  c = 4.2949;  d = 12.1672;  r2 = 2.78485;  r3 = 1.55107;  y3 = 6.94153

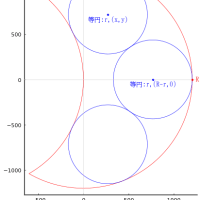
答曰では，小円の直径を 3.8497有奇としているが，その解に近い図は下のようになる。

パラメータは，以下のとおりである。
大円の直径が 10 のとき，小円の直径は 3.86769 である。中円の直径は 6.21908 である。
r1 = 5;  a = 13.1965;  b = 15.9957;  c = 5.01652;  d = 16.0811;  r2 = 3.10954;  r3 = 1.93385;  y3 = 8.01398

解が一意にならない原因は，この図形の条件として，大円の直径一つだけでは解は無数にあるということであろう。制約条件がもう一つ必要である。

function draw(r1, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (a, b, c, d, r2, r3, y3) = res[1]
   @printf("大円の直径が %g のとき，小円の直径は %g である。中円の直径は %g である。\n", 2r1, 2r3, 2r2)
   @printf("r1 = %g;  a = %g;  b = %g;  c = %g;  d = %g;  r2 = %g;  r3 = %g;  y3 = %g\n", r1, a, b, c, d, r2, r3, y3)
   plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:green, lw=0.5)
   circle(r1, b - r1, r1)
   circle(r2, r2, r2, :blue)
   circle(a - r2, r2, r2, :blue)
   circle(a - r3, y3, r3, :magenta)
   segment(c, 0, a, d, :orange)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, b - r1, "大円:r1,(r1,b-r1)", :red, :center, delta=-delta)
       point(r2, r2, "中円:r2,(r2,r2)", :blue, :center, delta=-delta)
       point(a - r2, r2, "中円:r2,(a-r2,r2)", :blue, :center, delta=-delta)
       point(a - r3, y3, "小円:r3\n(a-r3,y3)", :magenta, :center, :bottom, delta=delta)
       point(a, b, "(a,b)", :green, :right, :bottom, delta=delta/2)
       point(a, d, "(a,d)", :green, :right, :bottom, delta=delta/2)
       point(c, 0, "(c,0)", :green, :left, :bottom, delta=delta/2, deltax=2delta)
   end  
end;

draw(10/2, true)