算額（その833）

算額（その833）

藤田貞資(1807)：続神壁算法
http://www.wasan.jp/jinpeki/zokujinpekisanpo.pdf

長方形の一隅から直角三角形を切り取ると，残長（長辺から切り取られた残りの長さ）が 339.52 寸，残平（短辺から切り取られた残りの長さ）が 169.76 寸，截斜（切り取られた直角三角形の斜辺）の長さが 424.4 寸とする。切り取られたあとの面積が最大になるときの長方形の長辺の長さはいかほどか。

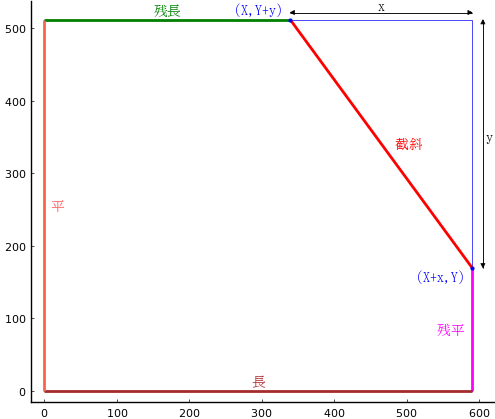
残長，残平，截斜をそれぞれ X, Y, L
長辺，短辺から切り取られる長さをそれぞれ x, y
切り取られたあとの面積を S とする。S は x の関数として表すことができる。S(x) = (X + x)*(Y + y) - x*y/2

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy
@syms x::positive, y::positive, S::positive
@syms X::positive, Y::positive, L::positive,
     x::positive, y::positive, S::positive
(X, Y, L) = (33952, 16976, 42440) .// 100
y = sqrt(L^2 - x^2)
S = (X + x)*(Y + y) - x*y/2;
pyplot(size=(300, 150), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(S, xlims=(200, 300), xlabel="x", ylabel="S(x)")

面積 S(x) は x = 250 前後で最大値をとる。最大値を取るときの x の値は，S(x) を x で微分し，S'(x) = 0 となる x を求めればよい。

x = 250.930000785733 のときに最大値を取ることがわかる。

x = solve(diff(S, x))[1].evalf()
x |> println

   250.930000785733

長方形のもとの長辺の長さは X + x なので，590.450000785733 である。

X + x |> println

   590.450000785733

その他のパラメータは以下のとおりである。

   長辺 = 590.45;  短辺 = 512.031;  残長 = 339.52;  残平 = 169.76;  截斜 = 424.4;  x = 250.93;  y = 342.271
   面積 = 302328.7537

function draw(more)
    pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (X, Y, L) = (33952, 16976, 42440) .// 100
   x = 250.930000785733
   y = sqrt(L^2 - x^2)
   @printf("長辺 = %g  短辺 = %g;  残長 = %g;  残平 = %g;  截斜 = %g;  x = %g;  y = %g\n", X + x, Y + y, X, Y, L, x, y)
   @printf("面積 = %.10g\n", (X + x)*(Y + y))
   plot([0, X + x, X + x, 0, 0], [0, 0, Y + y, Y + y, 0], color=:blue, lw=0.5)
   segment(X, Y + y, X + x, Y, :red, lw=2)
   segment(0, Y + y, X, Y + y, :green, lw=2)
   segment(X + x, 0, X + x, Y, :magenta, lw=2)
   segment(0, 0, X + x, 0, :brown, lw=2)
   segment(0, 0, 0, Y + y, :tomato, lw=2)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       #hline!([0], color=:gray80, lw=0.5)
       #vline!([0], color=:gray80, lw=0.5)
       dimension_line(X, Y + y + 10, X + x, Y + y + 10, "x", vertical=:bottom)
       dimension_line(X + x + 15, Y, X + x + 15, Y + y, "  y", vertical=:bottom)
       point(X, Y + y, "(X,Y+y) ", :blue, :right, :bottom, delta=delta/2)
       point(X + x, Y, "(X+x,Y) ", :blue, :right, delta=-delta/2)
       point(X/2, Y + y, "残長", :green, :center, :bottom, delta=delta/2, mark=false)
       point((X + x)/2, 0, "長", :brown, :center, :bottom, delta=delta/2, mark=false)
       point(X + x, Y/2, "残平 ", :magenta, :right, :vcenter, mark=false)
       point(0, (Y + y)/2, " 平", :tomato, :left, :vcenter, mark=false)
       point(X + x/2, Y + y/2, "  截斜", :red, :left, :vcenter, mark=false)
   end
end;

算額（その832）

算額（その832）

七八 加須市大字外野 棘脱地蔵堂 明治9年(1876)
埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

埼玉の算額78 加須市外野 棘脱地蔵堂 第1問
和算問題あれこれ2 令和６年４月の問題-No.２
https://gunmawasan.web.fc2.com/k-n-mondai.html

大円 2 個，中円 2 個が互いに交差し，できた区画に小円が 3 個入っている。
中円，小円の直径がそれぞれ 6 寸，3 寸のとき，大円の直径はいかほどか。

見た目によらず一本の方程式を解けばよいだけの簡単な問題である。

include("julia-source.txt");
# julia-source.txt ソース　https://blog.goo.ne.jp/r-de-r/e/ad3a427b84bb416c4f5b73089ae813cf

using SymPy

@syms r1::positive, r2::positive, r3::positive
eq1  = (r1 - r3)^2 + (r2 + 2r3)^2 - (r1 + r3)^2;
res = solve(eq1, r1)

   1-element Vector{Sym{PyCall.PyObject}}:
    (r2 + 2*r3)^2/(4*r3)

大円の直径は，「小円の直径の2倍に中円の直径を加えたものを二乗し，小円の直径の4倍で割る」ことにより得られる。

中円，小円の直径がそれぞれ 6 寸，3 寸のとき，大円の直径は = (2\*3 + 6)^2/(4\*3) = 12 寸である。

(2*3 + 6)^2/(4*3)

   12.0

function draw(more)
    pyplot(size=(500, 500), grid=false, showaxis=true, aspectratio=1, label="", fontfamily="IPAMincho")
   (r2, r3) = (6, 3) ./ 2
   r1 = (r2 + 2*r3)^2/(4*r3)
   @printf("大円の直径 = %g\n", 2r1)
   @printf("r1 = %g;  r2 = %g;  r3 = %g\n", r1, r2, r3)
   plot()
   circle2(r1 - r3, 0, r1)
   circle22(0, r3 + r2, r2, :blue)
   circle22(0, r2 + 2r3, r3, :green)
   circle(0, 0, r3, :green)
   if more == true
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1 - r3, 0, "大円:r1,(r1-r3,0)", :red, :center, delta=-delta)
       point(0, r3 + r2, "  中円:r2,(0,r3+r2)", :blue, :left, :vcenter)
       point(0, 2r3 + r2, " 小円:r3,(0,2r3+r2)", :green, :left, :bottom, delta=delta)
       point(0, r3, "r3", :green, :center, :bottom, delta=delta)
   end
end;

キーワード：とげぬき地蔵，とげ抜き地蔵，算額，埼玉