算額(その840)
九十七 岩手県大船渡市猪川町 雨宝堂(現雨宝山竜宝院) 文政7年(1824)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市. http://www.wasan.jp/yamamura/yamamura.html
キーワード:円9個,外円
大円内に中円 1 個,小円 7 個を入れる。すべての小円は大円に内接し,左右の一番下の小円は中円にも外接している。大円,小円の直径がそれぞれ 5 寸,1 寸のとき,中円の直径はいかほどか。
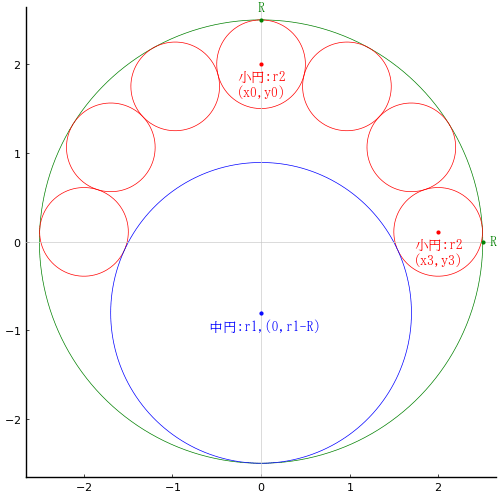
大円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を r1, (0, r1 - R)
小円の半径と中心座標を r2, (x0, y0), (x1, y1), (x2, y2), (x3, y3)
とおく。
注:小円の中心は大円の直径上にはない。
まず,隣り合う 2 個の小円の中心と大円の中心のなす角 2θ を求める。 例えば, (x0, y0), (0, 0), (x1, y1)
include("julia-source.txt")
using SymPy
@syms R::positive, r1::positive, r2::positive, θ::positive;
(R, r2) = (5, 1) .// 2
eq1 = (R - r2)*sind(θ) - r2
θ = solve(eq1, θ)[1]
θ |> println
180*asin(r2/(R - r2))/pi
右下端の小円の中心座標 (x3, y3) と中円が外接するという条件の方程式を解き,中円の半径を求める。
x3 = (R - r2)*cosd(90 - 6θ)
y3 = (R - r2)*sind(90 - 6θ)
eq2 = x3^2 + (y3 + (R - r1))^2 - (r1 + r2)^2;
res = solve(eq2, r1)[1]
res |> println
2*R*(R - r2)*cos(3*asin(r2/(R - r2)))^2/(R*cos(6*asin(r2/(R - r2))) + R - r2*cos(6*asin(r2/(R - r2))) + r2)
大円と小円の直径がそれぞれ 5 寸,1 寸のときに,中円の直径は 3.39195979899498 寸である。
2res(R => 5/2, r2 => 1/2) |> println
3.39195979899498
術では 3 + 78/197 = 3.3959390862944163 になっているが,図に描く限り差は認められない。
小数点以下第 3 位の 5 が 1 の誤記かどうかはわからないが,結構よい近似値になっている。
3 + 78/197
3.3959390862944163
function draw(more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(R, r2) = (5, 1) .// 2
plot()
circle(0, 0, R, :green)
θ = 180*asin(1/4)/pi
x = Vector{Float64}(undef, 4)
y = Vector{Float64}(undef, 4)
circle(0, R - r2, r2)
for i in 2:4
θ2 = 90 - (i - 1)*2θ
x[i] = (R - r2)*cosd(θ2)
y[i] = (R - r2)*sind(θ2)
circle2(x[i], y[i], r2)
end
r1 = 10*cos(3*asin(1/4))^2/(2*cos(6*asin(1/4)) + 3)
println("中円の直径 = $(2r1)")
circle(0, r1 - R, r1, :blue)
# r10 = (3 + 78/197)/2
# circle(0, r10 - R, r10, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
x3 = (R - r2)*cosd(90 - 6θ)
y3 = (R - r2)*sind(90 - 6θ)
point(0, R - r2, "小円:r2\n(x0,y0)", :red, :center, delta=-delta)
point(x3, y3, "小円:r2\n(x3,y3)", :red, :center, delta=-delta)
point(0, r1 - R, " 中円:r1,(0,r1-R)", :blue, :center, delta=-delta)
point(0, R, "R", :green, :center, :bottom, delta=delta)
point(R, 0, " R", :green, :left, :vcenter)
end
end;


















