算額（その857）

算額（その857）

二十二　岩手県一関市瑞山 駒形根神社 明治41年(1908)

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

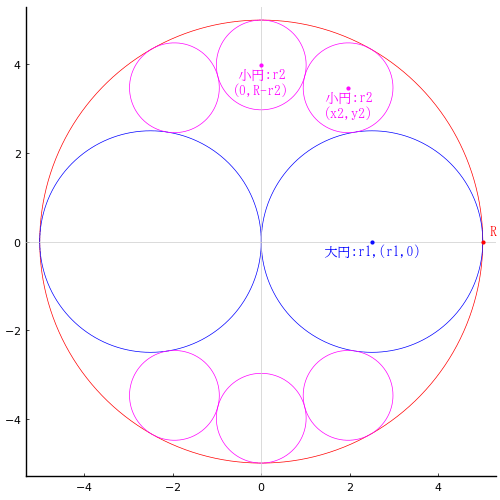
長方形の中に 2 本の弦と大円 1 個，小円 2 個を入れる。大円の直径が 1 寸のとき，小円の直径を求める術を述べよ。

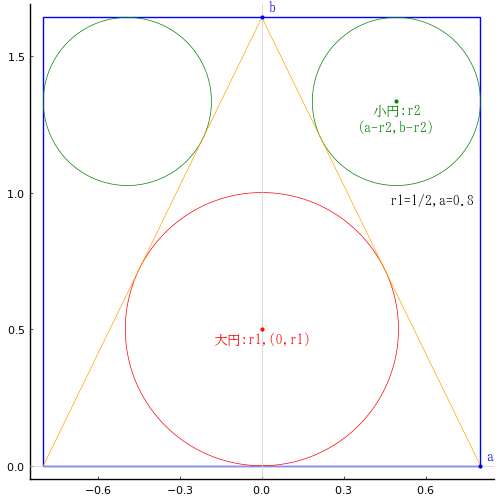
長方形の長辺と短辺を 2a, b
大円の半径と中心座標を r1, (0, r1)
小円の半径と中心座標を r2, (a - r2, b - r2)
とおき，以下の連立方程式を解く。
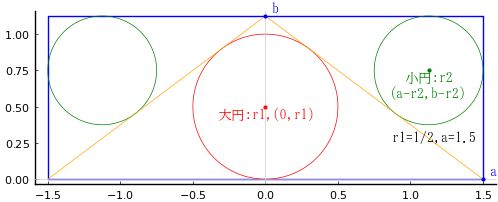
なお，分析結果からいうと，「大円の直径が 1 寸」という条件だけでは不足である。r1 が一定でも，a の値により小円の直径は変わる。つまり，この図形を決めるためには，大円の直径と長方形の長辺の両方が必要である。

include("julia-source.txt");

using SymPy

@syms a::positive, b::positive, r1::positive, r2::positive, d::positive
eq1 = dist(a, 0, 0, b, 0, r1) - r1^2
eq1 = numerator(apart(eq1, d))
eq2 = dist(a, 0, 0, b, a - r2, b - r2) - r2^2
eq2 = numerator(apart(eq2, d))
res = solve([eq1, eq2], (b, r2))

   2-element Vector{Tuple{Sym{PyCall.PyObject}, Sym{PyCall.PyObject}}}:
    (2*a^2*r1/((a - r1)*(a + r1)), a^2/(a - r1))
    (2*a^2*r1/((a - r1)*(a + r1)), a*r1/(a + r1))

2 組の解が得られるが，2 番目のものが適解である。
大円の直径が 1 寸で，長方形の長辺の長さが 2 寸のとき，小円の直径は 2/3 寸である。

r1 = 1/2  # 2r1 = 1
a = 1     # 2a = 2
2(a*r1/(a + r1))

   0.6666666666666666

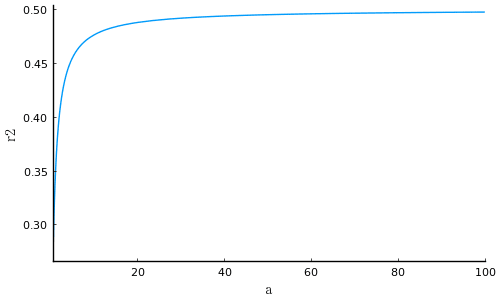
図に示すように，r1 が一定でも a が大きくなるにつれて r2 も大きくなり，0.5 に収束する。つまり，r2 の最大値は r1 で，小円の直径は大円の直径に近づいていく。

f = res[2][2](r1 => 1//2)
f |> println

   a/(2*(a + 1/2))

pyplot(size=(500, 300), showaxis=true, grid=false, aspectratio=:none, label="", fontfamily="IPAMincho")
plot(f, xlims=(0.6, 100), xlabel="a", ylabel="r2")

算額には「術」は書かれておらず，「答曰小円径六分〇九毛有奇」とのみある。山村は「図面は誤り。実証図はもっと大きい。」と書いているが，大円の直径に近づくとは気づいていない。

function draw(more=false)
   pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 1//2
   a = 1
   (b, r2) = (2*a^2*r1/(a^2 - r1^2), a*r1/(a + r1))
   @printf("小円の直径 = %g\n", 2r2)
   @printf("r1 = %g;  a = %g;  b = %g;  r2 = %g\n", r1, a, b, r2)
   plot([a, a, -a, -a, a], [0, b, b, 0, 0], color=:blue)
   circle(0, r1, r1)
   circle2(a - r2, b - r2, r2, :green)
   plot!([-a, 0, a], [0, b, 0], color=:orange, lw=0.5)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
       point(0, r1, "大円:r1,(0,r1)", :red, :center, delta=-delta/2)
       point(a - r2, b - r2, "小円:r2\n(a-r2,b-r2)", :green, :center, delta=-delta/2)
       point(a, b - 2.1r2, @sprintf("r1=1/2,a=%g ", a), :black, :right, mark=false)
   end
end;

算額（その856）

算額（その856）

二十二　岩手県一関市瑞山 駒形根神社 明治41年(1908)

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

外円内に大円 2 個，小円 6 個が入っている。外円の直径が 10 寸のとき，小円の直径を得る術を問う。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (r1, 0)
小円の半径と中心座標を r2, (0, R - r2), (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms R, r1, r2, x2, y2
r1 = R/2
eq1 = x2^2 + y2^2 - (R - r2)^2
eq2 = (r1 - x2)^2 + y2^2 - (r1 + r2)^2
eq3 = x2^2 + (R - r2 - y2)^2 - 4r2^2;
res = solve([eq1, eq2, eq3], (r2, x2, y2));

4 組の解が得られるが，2 番目のものが適解である。

(res[2][1](R=>5).evalf(),
res[2][2](R=>5).evalf(),
res[2][3](R=>5).evalf())

   (1.01331143350161, 1.96006569949517, 3.47157430856830)

それぞれは非常に長い式であるが，R が与えられれば小円の直径を求める「術」はある。以下のように計算すればよい。

# res[2][1] を求める関数を定義する

function 直径(R)
   f = ∛2
   h = f^2
   m = √69
   e = 69m + 997
   c = ∛e
   b = c^2
   a = 3h*b
   d = 330f + 37*c + a
   g = √d
   i = ∜d
   j = e^(5/6)
   k = d^(3/4)
   s = √e
   q = e^(1/6)
   r = (138m + 1994)^(2/3)
   n = sqrt(-a*g - 330f*g + 430*s + 74*c*g)
   o = sqrt(-207h*b*g - 22770f*g + 29670s + 5106c*g)
   p = sqrt(22770f + 2553c + 207h*b)
   R*(-17750573f*b*k*n/1242 - 154556461h*c*k*n/1242 - 2602054165k*n/1242 - 214763h*c*k*o/18 - 3923195k*o/18 - 21809f*b*k*o/18 - 4907453r*g/2 - 1625993r*p/6 - 341870903*c*g/9 - 11855327c*p/3 - 171811097f*g - 48431557f*p/3 + 658961h*m*s*i*n/9 + 28361659q*i*o/18 + 83669f*j*i*o/9 + 494602117h*s*i*n/621 + 18810834773q*i*n/1242 + 64451243f*j*i*n/621 + 8457376h*m*j + 488797196sqrt(4761*m + 68793)/3 + 1660341296f*m*q + 14095396844s/9 + 45213761744f*q/3 + 268114864h*j/3)/(19029096h*m*j + 366597897*m*s + 3735767916f*m*q + 3523849211s + 33910321308f*q + 201086148h*j)
end;
直径(10/2)

   1.01331143350161

算額では「術」はなく「答」も天下り式に「小円二寸」とある。
山村の記述では，「外円径÷5 = 小円径」としているが，こじつけである。

何度も経験することであるが，この文書に収められている算額および山村の記述には問題が多い。

function draw(more=false)
   pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 10/2
   r1 = R/2
   (r2, x2, y2) = (1.01331143350161, 1.96006569949517, 3.47157430856830)
   plot()
   circle(0, 0, R)
   circle2(r1, 0, r1, :blue)
   circle22(0, R - r2, r2, :magenta)
   circle4(x2, y2, r2, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(r1, 0, "大円:r1,(r1,0)", :blue, :center, delta=-delta/2)
       point(0, R - r2, "小円:r2\n(0,R-r2)", :magenta, :center, delta=-delta/2)
       point(x2, y2, "小円:r2\n(x2,y2)", :magenta, :center, delta=-delta/2)
   end
end;