算額（その893）

算額（その893）

七二 加須市大字外野 棘脱地蔵堂 明治7年(1874)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

大きさの同じ正三角形 2 個に挟まれて甲円と乙円がある。乙円は両方の正三角形の斜辺に外接し，甲円と内接している。

条件式は 1 個だけであり，正三角形の大きさには依存しない。
甲円と乙円の半径を r1, r2 として以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r1::positive, r2::positive
eq1 = r2/(2r1 - r2) - 1//2
res = solve(eq1, r2)[1]
res |> println

   2*r1/3

乙円の半径は甲円の半径の 2/3 倍である。
甲円の直径が 3 寸のと，乙円の直径は 2 寸である。

function draw(more=false)
   pyplot(size=(600, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 2
   r1 = 3//2
   r2 = 2r1/3
   plot([2a, a, 0, -a, -2a, 2a], [0, √3a, 0, √3a, 0, 0], color=:blue, lw=0.5)
   circle(0, r1, r1)
   circle(0, 2r1 - r2, r2, :green)
   circle(0, 0, 0.2r1, :blue, beginangle=0, endangle=60)
   circle(0, 0, 0.23r1, :blue, beginangle=0, endangle=60)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, "甲円:r1,(0,r1)", :red, :center, :bottom, delta=delta/2)
       point(0, 2r1 - r2, "乙円:r2,(0,2r1-r2)", :green, :center, :bottom, delta=2delta)
       point(0.25r1, 0.2r1, "60°", :blue, :left, :vcenter, mark=false)
   end
end;

算額（その892）

算額（その892）

七〇 加須市大字外野 棘脱地蔵堂 明治6年(1873)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

直角三角形内に全円 1 個，等円 2 個，両方の等円に接する斜線を入れる。全円，等円の直径がそれぞれ 2 寸，1.2 寸のとき，鈎（図のように置いたときの直角三角形の高さ）を求めよ。

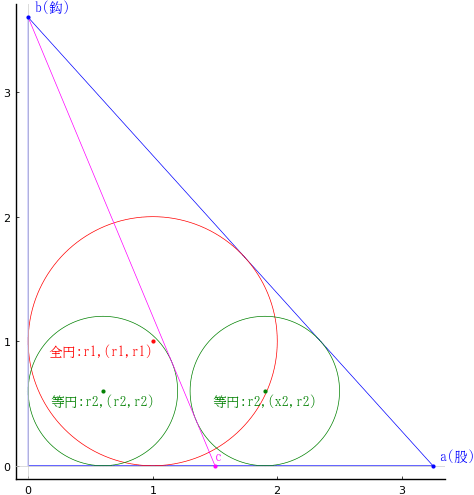
図のように置いたときの直角三角形の底辺の長さ，高さを a, b
斜線と底辺の交点座標を (c, 0)
全円の半径と中心座標を r1, (r1, r1)
等円の半径と中心座標を r1, (r2, r2), (x2, r2)
とおき，以下の連立方程式を解く。

1.　数値解を求める

条件を記述するときに r1, r2 の数値を代入した式にすれば，4 元連立方程式は解ける。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, c::positive, 弦::positive,
     r1::positive, r2::positive, x2::positive
(r1, r2) = (2//2, 12//20)
eq1 = b + c - sqrt(b^2 + c^2) - 2r2
eq2 = dist2(a, 0, 0, b, r1, r1, r1)
eq3 = dist2(a, 0, 0, b, x2, r2, r2)
eq4 = dist2(c, 0, 0, b, x2, r2, r2);
res = solve([eq1, eq2, eq3, eq4], (a, b, c, x2));
res[1]  # 1 of 3

   (13/4, 18/5, 3/2, 19/10)

鈎は 18/5 = 3.6 寸である。「答」では 3.7 寸になっているが，誤記である。
また，一般的には直角三角形の高さ（鈎）は底辺（股）より短いことが多いが，この図形においていは鈎のほうが長い。そして，算額の図は鈎が股より短く書かれているのでミスリーディングである。

2.　数式解を求める

18/5 がなぜ出てくるかは，r1, r2 を記号のままで 4 元連立方程式を解かなければならない。しかし，SymPy では自動的には解けないので，以下のように手動で解く。

方針としては，それぞれの方程式を眺めて，途中の式が複雑にならないものから変数を消去していき，最終的に b, r1, r2 だけを含む式を求める。

using SymPy
@syms a::positive, b::positive, c::positive, 弦::positive,
     r1::positive, r2::positive, x2::positive
eq1 = b + c - sqrt(b^2 + c^2) - 2r2
eq2 = dist2(a, 0, 0, b, r1, r1, r1)
eq3 = dist2(a, 0, 0, b, x2, r2, r2)
eq4 = dist2(c, 0, 0, b, x2, r2, r2);
eq1 |> println
eq2 |> println
eq3 |> println
eq4 |> println

   b + c - 2*r2 - sqrt(b^2 + c^2)
   a^2*b^2 - 2*a^2*b*r1 - 2*a*b^2*r1 + 2*a*b*r1^2
   a^2*b^2 - 2*a^2*b*r2 - 2*a*b^2*x2 + 2*a*b*r2*x2 - b^2*r2^2 + b^2*x2^2
   b^2*c^2 - 2*b^2*c*x2 - b^2*r2^2 + b^2*x2^2 - 2*b*c^2*r2 + 2*b*c*r2*x2

eq3, eq4 を対象にして x2 を消去する。

res_x2 = solve(eq4, x2)[2]  # 2 of 2
res_x2 |> println

   (c*(b - r2) + r2*sqrt(b^2 + c^2))/b

eq4 にはなかった sqrt(b^2 + c^2) が出てくる。これは，eq1 に出てくるので，b + c - 2r2 に置き換える。

res_x2 = res_x2(sqrt(b^2 + c^2) => (b + c - 2r2)) |> factor
res_x2 |> println

   -(-b*c - b*r2 + 2*r2^2)/b

eq3, eq4 の x2 に res_x2 を代入する。

eq13 = eq3(x2 => res_x2) |> simplify

   a^2*b^2 - 2*a^2*b*r2 - 2*a*b*(b*c + b*r2 - 2*r2^2) + 2*a*r2*(b*c + b*r2 - 2*r2^2) - b^2*r2^2 + (b*c + b*r2 - 2*r2^2)^2

eq14 = eq4(x2 => res_x2)/2r2^2 |> simplify
eq14 |> println

   b*c - 2*b*r2 - 2*c*r2 + 2*r2^2

eq14 を解いて c を求め，eq13 の c に代入する。代入後の eq13 = 0 は，eq13 の分子が 2 式の積になるので，どちらかが 0 であればよい。

res_c = solve(eq14, c)[1]
res_c |> println

   2*r2*(b - r2)/(b - 2*r2)

eq13(c => res_c) |> simplify |> numerator |> factor |> println

   (a*b - 2*a*r2 - 2*b*r2 + 2*r2^2)*(a*b^3 - 4*a*b^2*r2 + 4*a*b*r2^2 - 4*b^3*r2 + 12*b^2*r2^2 - 16*b*r2^3 + 8*r2^4)

t1 ≠ 0，t2 = 0 である。

t1 = a*b - 2*a*r2 - 2*b*r2 + 2*r2^2
t2 = a*b^3 - 4*a*b^2*r2 + 4*a*b*r2^2 - 4*b^3*r2 + 12*b^2*r2^2 - 16*b*r2^3 + 8*r2^4;

eq2 は a, b, r1 を含むので，a についてとき，これを t2 の a に代入する。

res_a = solve(eq2, a)[1]
res_a |> println

   2*r1*(b - r1)/(b - 2*r1)

t12 = t2(a => res_a) |> simplify
t12 |> println

   2*(b^3*r1*(b - r1) - 4*b^2*r1*r2*(b - r1) + 4*b*r1*r2^2*(b - r1) + 2*r2*(b - 2*r1)*(-b^3 + 3*b^2*r2 - 4*b*r2^2 + 2*r2^3))/(b - 2*r1)

これを b について求めると r1, r2 だけを含む式（解）になる。

res_b = solve(t12, b)[1]  # 1 of 4
res_b |> println

   -2*r2^2/(r1 - 2*r2)

これは「術曰置等円径自之等円径二段全円径差以除得鈎合問」すなわち「等円の直径を二乗したものを全円の直径と等円の直径の二倍との差で割る」
(2r1)^2/(2r1 - 2(2r2)) = 2r1^2/(r1 - 2r2) である。

r1 = 1, r2 = 0.6 を代入すると鈎(b) が得られる。すなわち，鈎は 3.6 寸である。

res_b(r1 => 1, r2 => 0.6) |> println

   3.60000000000000

以下，逆順に代入していくことで，すべての解を得ることができる。

res_a(r1 => 1, r2 => 0.6, b => 3.6) |> println

   3.25000000000000

res_c(r1 => 1, r2 => 0.6, b => 3.6, a => 3.25) |> println

   1.50000000000000

res_x2(r1 => 1, r2 => 0.6, b => 3.6, a => 3.25, c => 1.5) |> println

   1.90000000000000

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (1, 0.6)
   (a, b, c, x2) =  (13/4, 18/5, 3/2, 19/10)
   plot([0, a, 0, 0], [0, 0, b, 0], color=:blue, lw=0.5)
   circle(r1, r1, r1)
   circle(r2, r2, r2, :green)
   circle(x2, r2, r2, :green)
   segment(c, 0, 0, b, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, b, " b(鈎)", :blue, :left, :bottom, delta=delta/2)
       point(a, 0, " a(股)", :blue, :left, :bottom, delta=delta/2)
       point(c, 0, "c", :magenta, :left, :bottom, delta=delta/2)
       point(r1, r1, "全円:r1,(r1,r1)", :red, :right, delta=-delta/2)
       point(r2, r2, "等円:r2,(r2,r2)", :green, :center, delta=-delta/2)
       point(x2, r2, "等円:r2,(x2,r2)", :green, :center, delta=-delta/2)
   end
end;

 

算額（その891）

算額（その891）

七〇 加須市大字外野 棘脱地蔵堂 明治6年(1873)

埼玉県立図書館：埼玉県史料集 第二集『埼玉の算額』，昭和44年，誠美堂印刷所，埼玉県与野市.

外円の中に円弧 2 本，甲円，乙円各 2 個を入れる。乙円の径が□□甲円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (r1, 0), (0, r1)
乙円の半径と中心座標を r2, (x2, y2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive,
     r2::positive, x2::positive, y2::positive
eq1 = R - 2r1
eq2 = x2^2 + (R - y2)^2 - (R - r2)^2
eq3 = x2^2 + (r1 - y2)^2 - (r1 + r2)^2
eq4 = (x2 - r1)^2 + y2^2 - (r1 - r2)^2
res = solve([eq1, eq2, eq3, eq4], (R, r1, x2, y2))

   1-element Vector{NTuple{4, Sym{PyCall.PyObject}}}:
    (33*r2/4, 33*r2/8, 5*r2, 3*r2)

甲円の半径は乙円の半径の 33/8 倍である。

算額では乙円の直径は欠損文字であるが，「答曰甲円径三十二寸」とあるので，甲円の直径が 32 寸になるときの乙円の直径を逆算すると 256/33 = 7.75757757575 である。実に半端な数である。答が「甲円径三十三寸」の誤記ならば乙円の直径が 8 寸なので，丸く収まるのだが。
術も妥当なものではない。「術曰置乙円径四十三個以除八個二得甲円径合問」とあるが，これも「置乙円径三十三個以除八個乗甲円径」の誤記なら納得はできる。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 128/33
   (R, r1, x2, y2) = r2 .* (33/4, 33/8, 5, 3)
   @printf("乙円の直径が %g のとき，甲円の直径は %g\n", 2r2, 2r1)
   plot()
   circle(0, 0, R, :blue)
   circle(0, -R, R, beginangle=30, endangle=150)
   circle(0, R, R, beginangle=210, endangle=330)
   circle42(0, r1, r1, :magenta)
   circle4(x2, y2, r2, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, 0, "甲円:r1,(r1,0)", :magenta, :center, delta=-delta/2, deltax=6delta)
       point(0, r1, "甲円:r1,(r1,0)", :magenta, :center, :bottom, delta=delta/2)
       point(x2, y2, "乙円:r2,(x2,y2)", :black, :center, delta=-delta, deltax=-6delta)
       point(0, R, "R", :blue, :center, :bottom, delta=delta/2)
       point(R, 0, " R", :blue, :left, :bottom, delta=delta/2)
   end
end;