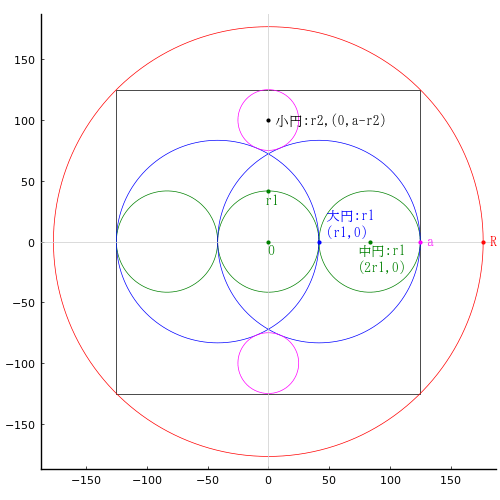
算額（その853）

算額（その853）

十七　岩手県平泉町 中尊寺金色堂（現存しない） 文政8年(1825)

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html

直角三角形（鈎股弦）内に隔斜を 2 本引き，区画された領域に等円を 2 個入れる。鈎，股，弦は，「5(鈎 + 股 + 弦) - 37(股 - 鈎) = 1」という条件式が成り立つとき（「鈎^2 + 股^2 = 弦^2」は当然），等円の直径はいかほどか。

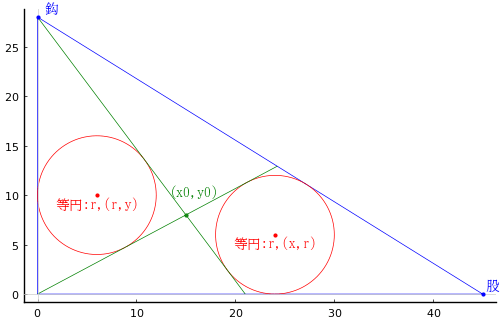
鈎股弦内に隔斜 2 本と等円 2 個を入れるという問は他にもある。算額（その139），算額（その280）

この算額では，鈎股弦の条件の出し方が独特である。

もし大学入試の数学の問題だと整数方程式を如何に効率的に解くかということになるかもしれないが，プログラムで全探索するほうが手っ取り早い。
念の為， 鈎，股 が 10000 まで探索すると，解は 28, 45, 53 の一組しかない。

include("julia-source.txt");
#=
mx = 10000
for 鈎 = 1:mx, 股 = 鈎 + 1:mx
   弦 = sqrt(鈎^2 + 股^2)
   if 5(鈎 + 股 + 弦) - 37(股 - 鈎) == 1
       @printf("%g;  %g;  %g\n", 鈎, 股, 弦)
   end
end
=#

鈎 = 28, 股 = 45 円の半径を r，それぞれの中心座標を (r, y), (x, r) とおき，直線までの距離に関する方程式を立て，解く。
SymPy の solve() では能力不足で解けないので，nlsolve() で数値解を求めるのが簡単であるが，変数を手動で消去していって r を求める手順を示してみよう。

まずは，式を簡単にするために，円の中心から隔斜までの距離の式を通覧する。

using SymPy

dist2(x1, y1, x2, y2, x3, y3, r) = numerator(apart(dist(x1, y1, x2, y2, x3, y3) - r^2, d))
@syms 鈎::positive, 股::positive, 弦::positive,
     r::positive, x::positive, y::positive, x0::positive, y0::positive,
     d;
eq1 = dist2(0, 鈎, x0, y0, r, y, r)  # 円1の中心から BD への距離
eq2 = dist2(0, 鈎, x0, y0, x, r, r)  # 円2の中心から BD への距離
eq3 = dist2(0, 鈎, 股,  0, x, r, r)  # 円2の中心から AB への距離
eq4 = dist2(0, 0,  x0, y0, r, y, r)  # 円1の中心から OC への距離
eq5 = dist2(0, 0,  x0, y0, x, r, r); # 円2の中心から OC への距離

println(eq1, ",  # eq1")
println(eq2, ",  # eq2")
println(eq3, ",  # eq3")
println(eq4, ",  # eq4")
println(eq5, ",  # eq5")

   -r^2*x0^2 - 2*r*x0*y*y0 + 2*r*x0*y*鈎 + 2*r*x0*y0*鈎 - 2*r*x0*鈎^2 + x0^2*y^2 - 2*x0^2*y*鈎 + x0^2*鈎^2,  # eq1
   -r^2*y0^2 + 2*r^2*y0*鈎 - r^2*鈎^2 - 2*r*x*x0*y0 + 2*r*x*x0*鈎 - 2*r*x0^2*鈎 + x^2*y0^2 - 2*x^2*y0*鈎 + x^2*鈎^2 + 2*x*x0*y0*鈎 - 2*x*x0*鈎^2 + x0^2*鈎^2,  # eq2
   -r^2*鈎^2 + 2*r*x*股*鈎 - 2*r*股^2*鈎 + x^2*鈎^2 - 2*x*股*鈎^2 + 股^2*鈎^2,  # eq3
   -r^2*x0^2 - 2*r*x0*y*y0 + x0^2*y^2,  # eq4
   -r^2*y0^2 - 2*r*x*x0*y0 + x^2*y0^2,  # eq5

最初に，eq5 を x について解く。

res1 = solve(eq5, x0)[1]
res1 |> println

   y0*(-r^2 + x^2)/(2*r*x)

eq1 〜 eq4 に x0 = y0*(-r^2 + x^2)/(2*r*x) を代入する。結果の方程式は eq11 〜 eq14

eq11 = numerator(apart(eq1(x0 => res1), d))/y0/(x - r)/(x + r) |> factor;

eq12 = numerator(apart(eq2(x0 => res1), d))/鈎/(x - r)/(x + r) |> factor;

eq13 = numerator(apart(eq3(x0 => res1), d))/鈎 |> factor;

eq14 = numerator(apart(eq4(x0 => res1), d))/y0^2/(x - r)/(x + r) |> factor;

次に eq14 を x について解く。

res2 = solve(eq14, x)[1]
res2 |>  println

   r*(r + y)/(-r + y)

eq11 〜 eq14 に x = r*(r + y)/(-r + y) を代入する。

eq21 = numerator(apart(eq11(x => res2), d))/(4r^3*鈎) |> factor;

eq22 = numerator(apart(eq12(x => res2), d))/(4r^3) |> factor;

eq23 = numerator(apart(eq13(x => res2), d)) |> factor;

次に eq21 を y0 について解く。

res3 = solve(eq21, y0)[1]
res3 |> println

   (-r^2*y + r^2*鈎 + y^3 - y^2*鈎)/(r^2 + y^2 - y*鈎)

eq21 〜 eq23 に y0 = (-r^2*y + r^2*鈎 + y^3 - y^2*鈎)/(r^2 + y^2 - y*鈎) を代入する。

eq32 = numerator(apart(eq22(y0 => res3), d))/(y*(r + y)^2) |> factor
eq32 |> println

   (-r^2 - 2*r*y + 2*r*鈎 + y^2 - y*鈎)*(-r^3 + r^2*y - r^2*鈎 - r*y^2 + r*鈎^2 + y^3 - y^2*鈎)

eq33 = numerator(apart(eq23(y0 => res3), d)) |> factor;

eq32 は 式1*式2 の形で，-r^2 - 2*r*y + 2*r*鈎 + y^2 - y*鈎 = 0 を解けばよい。

eq32_1 = (-r^2 - 2*r*y + 2*r*鈎 + y^2 - y*鈎);

eq32_1 を y について解く。

res4 = solve(eq32_1, y)[1]
res4 |> println

   r + 鈎/2 - sqrt(8*r^2 - 4*r*鈎 + 鈎^2)/2

eq33 に y = r + 鈎/2 - sqrt(8*r^2 - 4*r*鈎 + 鈎^2)/2 を代入する。

eq42 = eq33(y => res4) |> simplify
eq42 |> factor |> println

   (2*r*股 + 2*r*鈎 - 股*鈎)*(4*r^3 - 4*r^2*股 + 2*r^2*鈎 - 2*r^2*sqrt(8*r^2 - 4*r*鈎 + 鈎^2) + 2*r*股*鈎 - 股*鈎^2 + 股*鈎*sqrt(8*r^2 - 4*r*鈎 + 鈎^2))/2

sqrt(8*r^2 - 4*r*鈎 + 鈎^2) でまとめ，二乗してルートを外す。

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     r::positive, x::positive, y::positive, x0::positive, y0::positive

eq01 = (4*r^3 - 4*r^2*股 + 2*r^2*鈎  + 2*r*股*鈎 - 股*鈎^2)^2 - (股*鈎 - 2*r^2)^2*(8*r^2 - 4*r*鈎 + 鈎^2) |> factor
eq01 |> println

   -4*r^2*(4*r^4 + 8*r^3*股 - 8*r^3*鈎 - 4*r^2*股^2 - 8*r^2*股*鈎 + 4*r*股^2*鈎 + 4*r*股*鈎^2 - 股^2*鈎^2)

eq02 = eq01/(-4r^2)
eq02 |> println

   4*r^4 + 8*r^3*股 - 8*r^3*鈎 - 4*r^2*股^2 - 8*r^2*股*鈎 + 4*r*股^2*鈎 + 4*r*股*鈎^2 - 股^2*鈎^2

鈎，股に具体値を代入してプロットしてみる。

eq03 = eq02(鈎 => Sym(28), 股 => Sym(45))

   4*r^4 + 8*r^3*股 - 8*r^3*鈎 - 4*r^2*股^2 - 8*r^2*股*鈎 + 4*r*股^2*鈎 + 4*r*股*鈎^2 - 股^2*鈎^2

using Plots
pyplot(size=(400, 200), grid=false, aspectratio=:none, label="", fontfamily="IPAMincho");
plot(eq03, xlims=(4, 32))
hline!([0])

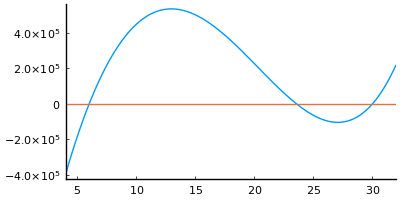
3 個の実数解が得られるが r = 6 が適解である。

solve(eq03, r)

   3-element Vector{Sym{PyCall.PyObject}}:
                   6
                  30
    -35 + 7⋅√70

あとは，交代代入を繰り返し，ここまでで変数消去されていた変数の値を確定していけばよい。

(鈎, 股) = (28, 45)
r = 6
y = r + 鈎/2 - sqrt(8*r^2 - 4*r*鈎 + 鈎^2)/2
y0 = (-r^2*y + r^2*鈎 + y^3 - y^2*鈎)/(r^2 + y^2 - y*鈎)
x = r*(r + y)/(-r + y)
x0 = y0*(-r^2 + x^2)/(2*r*x)
(r, y, y0, x, x0)

   (6, 10.0, 8.0, 24.0, 15.0)

NLsolve() で数値解を求めるほうが，簡単である。

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number</span>
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (r, x, y, x0, y0) = u
   return [
       -r^2*x0^2 - 2*r*x0*y*y0 + 2*r*x0*y*鈎 + 2*r*x0*y0*鈎 - 2*r*x0*鈎^2 + x0^2*y^2 - 2*x0^2*y*鈎 + x0^2*鈎^2,  # eq1
       -r^2*y0^2 + 2*r^2*y0*鈎 - r^2*鈎^2 - 2*r*x*x0*y0 + 2*r*x*x0*鈎 - 2*r*x0^2*鈎 + x^2*y0^2 - 2*x^2*y0*鈎 + x^2*鈎^2 + 2*x*x0*y0*鈎 - 2*x*x0*鈎^2 + x0^2*鈎^2,  # eq2
       -r^2*鈎^2 + 2*r*x*股*鈎 - 2*r*股^2*鈎 + x^2*鈎^2 - 2*x*股*鈎^2 + 股^2*鈎^2,  # eq3
       -r^2*x0^2 - 2*r*x0*y*y0 + x0^2*y^2,  # eq4
       -r^2*y0^2 - 2*r*x*x0*y0 + x^2*y0^2,  # eq5
   ]
end;

(鈎, 股, 弦) = (28, 45, 53)
iniv = BigFloat[5.0, 20, 11, 12, 10]
res = nls(H, ini=iniv)

   ([6.0, 24.0, 10.0, 15.0, 8.0], true)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (鈎, 股, 弦) = (28, 45, 53)
   (r, x, y, x0, y0) = res[1]
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:blue, lw=0.5)
   circle(r, y, r)
   circle(x, r, r)
   (X1, Y1) = intersection(0, 0, x0, y0, 0, 鈎, 股, 0)
   segment(0, 0, X1, Y1, :green)
   (X2, Y2) = intersection(0, 鈎, x0, y0, 0, 0, 股, 0)
   segment(0, 鈎, X2, Y2, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x, r, "等円:r,(x,r)", :red, :center, delta=-delta/2)
       point(r, y, "等円:r,(r,y)", :red, :center, delta=-delta/2)
       point(x0, y0, "(x0,y0)", :green, :left, :bottom, delta=4delta, deltax=-4delta)
       point(股, 0, " 股", :blue, :left, :bottom, delta=delta/2)
       point(0, 鈎, " 鈎", :blue, :left, :bottom, delta=delta/2)
   end
end;

算額（その852）

算額（その852）

十六　岩手県前沢町赤生津箱根 金刀比羅神社 明治43年(1910)

山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

外円の中に正方形，さらにその中に 7 個の円が入っている。小円の直径が 50 寸のとき，外円の直径はいくつか。

算額（その77）を 90 度回転し，外円を加えたものに過ぎない。求めるものも，外円の直径になっている。

外円の半径と中心座標を R, (0, 0)
正方形の一辺の長さを 2a = √2R
大円の半径と中心座標を r0, (r1, r0), (-r1, r0); r0 = 2r1
中円の半径と中心座標を r1, (0, 0), (r0, r1)
小円の半径と中心座標を r2, (0, a - r2)
とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, a::positive, r1::positive, r2::positive;
a =  R/sqrt(Sym(2))
r1 = a/3
eq1 = r1^2 + (a - r2)^2 +  - (2r1 + r2)^2
res = solve(eq1, R)[1]
res |> println

   5*sqrt(2)*r2

外円の直径は 小円の直径の 5√2 倍である。
小円の直径が 50 寸のとき，外円の直径は 353.5533905932738 になる。
√2 ≒ 1.414 で近似すると 353.5 である。

しかし，（判読不能箇所が多いが）問の末尾近くの一部分には「▢▢只▢五十二有寸外円径問幾何」とあり，52というのは小円の径を言っているのだろうと推測される。小円の径が 52 なら，外円の径は 353.5 にはならない。
術は「置二個開平方乗小円径五段得外円径」と正しいことをいっているのだが。

なお，正方形の長さは小円の直径の 3 倍，中円の直径は小円の直径の 5/3 倍である。

50*5*1.414, 50*5√2

   (353.5, 353.5533905932738)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 50//2
   R = 5√2r2
   a = R/√2
   r1 = a/3
   @printf("外円の直径 = %g;  正方形の一辺の長さ = %g;  中円の直径 = %g;  小円の直径 = %g\n", 2R, 2a, 2r1, 2r2)
   plot(a .* [-1, 1, 1, -1, -1], a .* [-1, -1, 1, 1, -1], color=:black, lw=0.5)
   circle(0, 0, R)
   circle(0, 0, r1, :green)
   circle2(a - r1, 0, r1, :green)
   circle2(r1, 0, 2r1, :blue)
   circle22(0, a - r2, r2, :magenta)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, 0, " O", :green, :center, delta=-delta/2)
       point(r1, 0, " 大円:r1\n (r1,0)", :blue, :left, :bottom, delta=delta/2)
       point(0, r1, " r1", :green, :center, delta=-delta/2)
       point(2r1, 0, "中円:r1\n(2r1,0)", :green, :left, deltax=-2delta, delta=-delta/2)
       point(0, a - r2, " 小円:r2,(0,a-r2)", :black, :left, :vcenter)
       point(a, 0, " a ", :magenta, :left, :vcenter)
       point(R, 0, " R ", :red, :left, :vcenter)
   end
end;