算額（その873）

算額（その873）

会田安明：算法天生法指南，文化7年(1810)
京都大学貴重資料デジタルアーカイブ
https://rmda.kulib.kyoto-u.ac.jp/item/rb00028519#?c=0&m=0&s=0&cv=95&r=0&xywh=-487%2C-149%2C4481%2C2977

横長の紙をおみくじ状に結ぶ。紙の幅が一寸のとき正五角形の一辺の長さはいかほどか。

正五角形の一辺の長さ(ab)を x，紙の幅(ac)を y とする。
図において，∠bac = 18° である。
x*cosd(18) = y より，y が与えられたとき x = 2√2y/sqrt(√5 + 5)を求める。

include("julia-source.txt");

using SymPy
@syms x, y
eq = x*cosd(Sym(18)) - y
x = solve(eq, x)[1]
x |> println

   2*sqrt(2)*y/sqrt(sqrt(5) + 5)

紙の幅が 1 寸のとき，正五角形の一辺の長さは 1.0514622242382672 寸である。

x(y => 1).evalf() |> N

   1.0514622242382672

算額（その872）

算額（その872）

大阪府茨木市 井於神社 弘化3年(1846)
http://www.wasan.jp/osaka/iyo.html

大球の中に，小球 3 個と，中球 1 個が入っている。大球と小球の直径がそれぞれ 1 尺 2 寸と 4 寸 8 分のとき，中球の直径を求めよ。

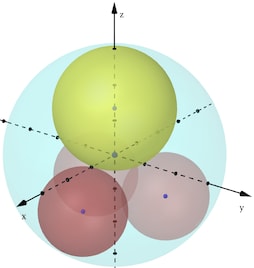
eq1, eq2: y 軸の負の無限大方向から x-z 平面を見ると，小球は大球に内接し，中級と外接している。

eq3: 3 次元空間，x-y-z 軸で考える。z 軸の正の無限大方向から x-y 平面を見ると，小球 3 個は互いに接しており，その中心を結ぶと正三角形になる。

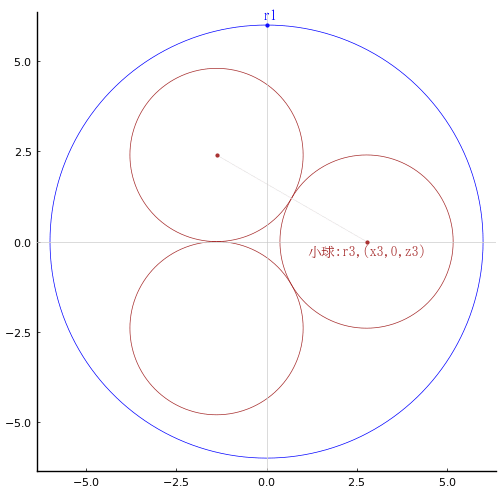
大球の半径と中心座標を r1, (0, 0, 0)
中球の半径と中心座標を r2, (0, 0, r1 - r2)
小球の半径と中心座標を r3, (x3, 0, z3); z3 < 0
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive, x3::positive, z3::negative
(r1, r3) = (120, 48) .// 20
eq1 = x3^2 + z3^2 - (r1 - r3)^2
eq2 = x3^2 + (r1 - r2 - z3)^2 - (r2 + r3)^2
eq3 = x3√Sym(3)/2 - r3
(r2, x3, z3) = solve([eq1, eq2, eq3], (r2, x3, z3))[1]

   (3*sqrt(33)/17 + 39/17, 8*sqrt(3)/5, -2*sqrt(33)/5)

中球の直径は 2(3√33 + 39)/17  = 6.615727992895775 寸である。

2(3√33 + 39)/17

   6.615727992895775

算額の「答」は「中球径七寸二分」となっているが，これは中球と小球の 1 個が大球の直径上に並ぶ解（12 尺 = 7.2 + 4.8）で，残りの 2 個の小球が入る余地がない。「術」の記述はない。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3) = (120, 48) .// 20
   (r2, x3, z3) = (3*sqrt(33)/17 + 39/17, 8*sqrt(3)/5, -2*sqrt(33)/5)
   plot()
   circle(0, 0, r1, :blue)
   circle(0, r1 - r2, r2, :orange)
   circle(x3, z3, r3, :brown)
   if more        
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, " r1", :blue, :center, :bottom, delta=delta/2)
       point(0, r1 - r2, "中球:r2,(0,0,r1-r2)", :orange, :center, delta=-delta/2)
       point(x3, z3, "小球:r3,(x3,0,z3)", :brown, :center, delta=-delta/2)
   end
end;

function draw2(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3) = (120, 48) .// 20
   (r2, x3, z3) = (3*sqrt(33)/17 + 39/17, 8*sqrt(3)/5, -2*sqrt(33)/5)
   plot()
   circle(0, 0, r1, :blue)
   rotate(x3, 0, r3, :brown)
   (x, y) = x3*cosd(120), x3*sind(120)
   segment(x, y, x3, 0, :gray90)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, r1, " r1", :blue, :center, :bottom, delta=delta/2)
       point(x3, 0, "小球:r3,(x3,0,z3)", :brown, :center, delta=-delta/2)
       point(x, y, "", :brown)
   end
end;