算額(その887)
六四 加須市不動岡 総願寺 慶応2年(1866)
埼玉県立図書館:埼玉県史料集 第二集『埼玉の算額』,昭和44年,誠美堂印刷所,埼玉県与野市.
キーワード:円8個,正方形,菱形
#Julia, #SymPy, #算額, #和算
長方形内に菱形 1 個,甲円 4 個,乙円 2 個,丙円 2 個を入れる。長方形の長辺と短辺が 15 寸,14 寸のとき,甲円の直径はいかほどか。

長方形の長辺と短辺を 2a, 2b
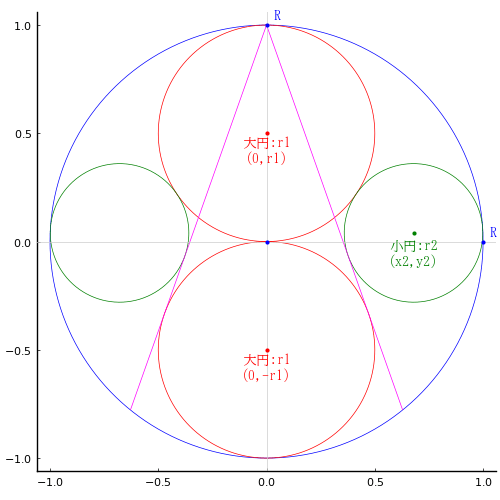
甲円の半径と中心座標を r1, (a - r1, b - r1)
乙円の半径と中心座標を r2, (0, b - r2)
丙円の半径と中心座標を r3, (a - r3, 0)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, b::positive,
r1::positive, r2::positive, r3::positive
#@syms a, b, r1, r2, r3
eq1 = (r1 - r3)^2 + (b - r1)^2 - (r1 + r3)^2
eq2 = (a - r1)^2 + (r1 - r2)^2 - (r1 + r2)^2
eq3 = dist2(a - 2r3, 0, 0, b - 2r2, a - r1, b - r1, r1);
1. 三元連立方程式を解く
7 組の解が得られるが,最初のもののみが適解である。
なお,解を求める順番の指定が必須である。solve([eq1, eq2, eq3], (r1, r2, r3)) とすると,有限の時間ないには解が得られないようだ。
res = solve([eq1, eq2, eq3], (r2, r3, r1))[1]; # 1 of 7
r2
res[1] |> display
r3
res[2] |> display
r1
res[3] |> display
実際に数値解を求めるには,一時変数を定義すれば若干簡単になる。
長辺,短辺が 2a = 15 寸,2b = 14 寸のとき,甲円,乙円,丙円の直径 d1,d2,d3 は以下のようになる。
(a, b) = (Sym(15)/2, Sym(14)/2)
t = sqrt(a^2 + 6a*b + b^2)
u = (a + b)t - 4a*b
v = a^2 - b^2
d1 = t - a - b
d2 = (u + v)/4b
d3 = (u - v)/4a
(d1, d2, d3)
(6, 27/8, 8/3)
なお,次項に示すように,r2, r3 と r1 の関係式を用いれば,d1 を求めた後に d2, d3 を求めてもよい。
d2 = (a - d1/2)^2/d1
d3 = (b - d1/2)^2/d1
長方形の長辺,短辺が 15 寸, 14 寸のとき,甲円の直径は 6 寸である。
なお,乙円,丙円の直径はそれぞれ 27/8 寸,8/3 寸である。
2. 別解
まず,eq1, eq2 を連立方程式として r2, r3 を求める。
r2, r3 は以下のように,r1 を用いて表すことができる。
res2 = solve([eq1, eq2], (r2, r3));
r2
res2[r2] |> factor |> display
r3
res2[r3] |> factor |> display
eq3 にこれらを代入し r1 について解く。
7 通りの解が得られるが,下記のものが唯一の適解である。
r1
solve(eq3(r2 => res2[r2], r3 => res2[r3]), r1)[1] # 1 of 7
まとめると,長辺,短辺が 2a,2b のとき,甲円,乙円,丙円の半径 r1, r2, r3 は以下の通りである。
r1 = (sqrt(a^2 + 6*a*b + b^2) - a - b)/2
r2 = (a - r1)^2/4r1
r3 = (b - r1)^2/4r1
3. 考察
r1 は,a, b から計算されるが,a, b にどんな値を与えても良いものではない。
r1 = (sqrt(a^2 + 6*a*b + b^2) - a - b)/2
計算される r1 が,2r1 > a または 2r1 > b となる場合は,不適切解になる(解はない)。
function draw(a, b, more=false)
pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r1 = (sqrt(a^2 + 6*a*b + b^2) - a - b)/2
if 2r1 > a || 2r1 > b
println("不適切な図になります")
return
end
r2 = (a - r1)^2/4r1
r3 = (b - r1)^2/4r1
@printf("長方形の長辺,短辺が %g, %g のとき,甲円の直径は %g である\n", 2a, 2b, 2r1)
@printf("a = %g; b = %g; r1 = %g; r2 = %g; r3 = %g\n", a, b, r1, r2, r3)
plot([a, a, -a, -a, a], [-b, b, b, -b, -b], color=:blue, lw=0.5)
plot!([0, a - 2r3, 0, 2r3 - a, 0], [2r2 - b, 0, b - 2r2, 0, 2r2 - b], color=:orange, lw=0.5)
circle4(a - r1, b - r1, r1, :green)
circle22(0, b - r2, r2)
circle2(a - r3, 0, r3, :magenta)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
point(0, b, " b", :blue, :left, :bottom, delta=delta/2)
point(a - r1, b - r1, "甲円:r1,(a-r1,b-r1)", :green, :center, :bottom, delta=delta/2)
point(0, b - r2, "乙円:r2\n(0,b-r2)", :red, :center, :bottom, delta=delta/2)
point(a - r3, 0, "丙円:r3\n(a-r3,0)", :magenta, :center, :bottom, delta=delta/2)
end
end;
draw(15/2, 14/2, true)