算額（その855）
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市. http://www.wasan.jp/yamamura/yamamura.html
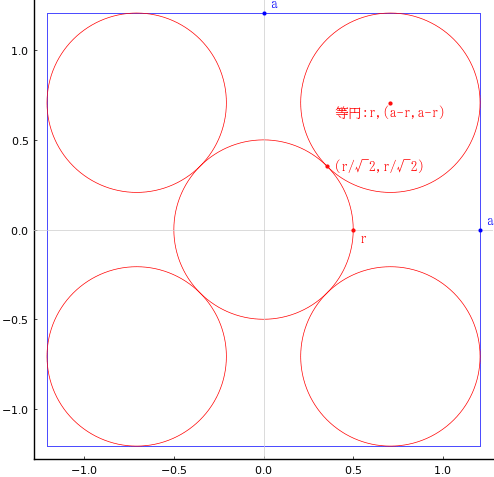
正方形内に直径が 1 寸の 4 個の等円を入れる。赤で示した部分の面積を求めよ。
正方形の一辺の長さを 2a，等円の半径を r とおくと，正方形の一辺の長さは等円の直径の 1 + √2 倍である。
include("julia-source.txt");
using SymPy
@syms a, r
eq = (2r)^2 - 2(a - r)^2
a = solve(eq, a)[2]
a |> println
r*(1 + sqrt(2))
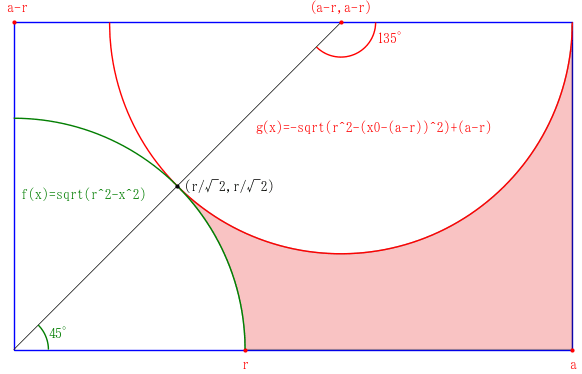
赤積は，点 (0, 0), (a, 0), (a, a - r), (a - r, a - r) を結んでできる台形の面積から，緑で示した等円の面積の 45/360 と，赤で示した等円の面積の 135/360 を引いたものである。
赤積 = 2((a + r)*(a - r)/2 - pi*r^2*(1/8 + 135/360)) = (a^2 - r^2) - pi*r^2
r = 1/2 のとき，a = 1 + √2 なので，赤積 = 0.4217086177890992 である。
r = 1/2
a = r*(1 + sqrt(2))
(a^2 - r^2) - pi*r^2
0.4217086177890992
また，緑の等円の（上側の）方程式 f(x) と 赤の等円の（下側）の方程式 g(x) について積分することで，赤積を求めることもできる。
当然ながら両者は一致する。
@syms r, a, x, f, g
r = 1//2
a = r*(1 + √Sym(2))
f = sqrt(r^2 - x^2)
S1 = integrate(f, (x, r/√(Sym(2)), r));
S1 |> println
g = -sqrt(r^2 - (x - (a - r))^2) + (a - r)
S2 = integrate(g, (x, r/√(Sym(2)), a));
S2 |> println
S = S2 - S1
S |> println
2S.evalf() |> println
-1/16 + pi/32
-5/16 - 3*pi/32 + sqrt(2)*(1/2 + sqrt(2)/2)/2
-pi/8 - 1/4 + sqrt(2)*(1/2 + sqrt(2)/2)/2
0.421708617789099
念の為，GeoGebra で図形を描き，面積を多角形で近似すると，ほぼ同じ数値になることを確かめた。
答曰も，術曰も赤積は 0.884 有奇としているが，明白な誤りである。
0.7854 は円積率で，0.7854 * 4 は円周率に極めて近い数値なのであるが，ほかは何を計算しているのだろうか。
(sqrt(0.75) + 1 - 0.7854 * 1.25) |> println
sqrt(0.75) + 1 |> println
0.7854 * 4 |> println
0.7854 * 1.25 |> println
1.866 - 0.98175 |> println
0.8842754037844386
1.8660254037844386
3.1416
0.98175
0.8842500000000001
function draw(more=false)
pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
r = 1//2
a = r*(1 + sqrt(2))
赤積 = 2((a + r)*(a - r)/2 - pi*r^2*(1/8 + 135/360))
println("赤積 = $赤積")
plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:blue, lw=0.5)
circle4(a - r, a - r, r)
circle(0, 0, r)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
point(0, a, " a", :blue, :left, :bottom, delta=delta/2)
point(a - r, a - r, "等円:r,(a-r,a-r)", :red, :center, delta=-delta/2)
point(r/√2, r/√2, " (r/√2,r/√2)", :red, :left, :vcenter)
point(r, 0, " r", :red, :left, delta=-delta/2)
end
end;
