算額(その859)
山村善夫:現存 岩手の算額,昭和52年1月30日,熊谷印刷,盛岡市. http://www.wasan.jp/yamamura/yamamura.html
長方形内に大円が内接する不等辺三角形を入れ,大きさの同じ小円を左側に複数個,右側に 1 個入れる。小円の直径がわかっているとき,左側の小円の個数と大円の直径を求めよ。
なお,前もって述べるが,術では「(左側の小円の個数÷2 + 1)×小円径=大円径」とあるが,この式は一般には成り立たない。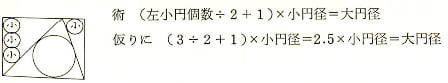
また,左側の小円の個数が 1 個の場合は「算額(その857)」と同じになるが,その場合も,算額(その857)で述べた通り,示された条件だけでは不足であり,たとえば長方形の長辺の長さが既知でなければ一意な解はない。さらに,左側の小円の個数も未知として方程式を解くことは適切とは思えない。小円の個数も与えたうえで大円の直径を求めよとするのが妥当であろう。
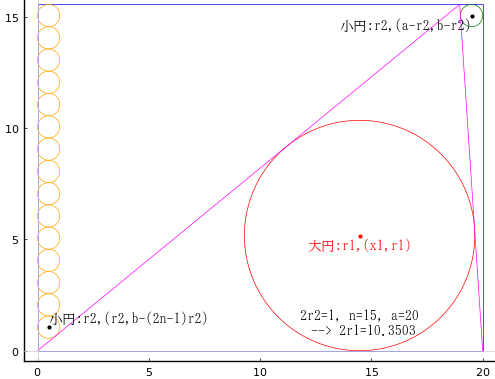
長方形の長辺と短辺の長さを a, b
不等辺三角形の頂点の座標を (c, b)
大円の半径と中心座標を r1, (x1, r1)
小円の半径と中心座標を r2, (r2, b - (2n - 1)*r2), (a - r2, b - r2)
とおき,以下の連立方程式を解く。
include("julia-source.txt");
using SymPy
@syms a::positive, b::positive, c::positive, n::integer,
r1::positive, x1::positive, r2::positive, d
l1 = sqrt(b^2 + c^2)
l2 = sqrt(b^2 + (a - c)^2)
S1 = (a + l1 + l2)*r1/2
S2 = (b + c*(2n - 1) + l1)*r2/2
S3 = ((a - c) + b + l2)*r2/2
eq1 = (S2 + S3) - S1
eq2 = numerator(apart(dist(0, 0, c, b, x1, r1) - r1^2, d))
eq3 = numerator(apart(dist(c, b, a, 0, x1, r1) - r1^2, d))
eq4 = numerator(apart(dist(c, b, a, 0, a - r2, b - r2) - r2^2, d))
eq5 = (a - c) + b - l2 - 2r2;
using NLsolve
function nls(func, params...; ini = [0.0])
if typeof(ini) <: Number
r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
v = r.zero[1]
else
r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
v = r.zero
end
return Float64.(v), r.f_converged
end;
function H(u)
(b, c, r1, x1) = u
return [
-r1*(a + sqrt(b^2 + c^2) + sqrt(b^2 + (a - c)^2))/2 + r2*(b + c*(2*n - 1) + sqrt(b^2 + c^2))/2 + r2*(a + b - c + sqrt(b^2 + (a - c)^2))/2, # eq1
-b^2*r1^2 + b^2*x1^2 - 2*b*c*r1*x1, # eq2
a^2*b^2 - 2*a^2*b*r1 - 2*a*b^2*x1 + 2*a*b*c*r1 + 2*a*b*r1*x1 - b^2*r1^2 + b^2*x1^2 - 2*b*c*r1*x1, # eq3
a + b - c - 2*r2 - sqrt(b^2 + (a - c)^2), # eq5
]
end;
左側の小円が 1 個の場合に,算額(その857)と同じになる。
算額(その857)は大円の直径から小円の直径を求めるものであるが,長方形の長辺が 2,大円の直径が 1 のとき,小円の直径が 2/3 である。
本算額では,以下のように小円の直径から大円の直径を求めることになる。
a = 2
n = 1
r2 = 1/3
iniv = BigFloat[2, 1.5, 0.6, 1.2]
res = nls(H, ini=iniv)
([1.3333333333333333, 1.0, 0.49999999999999994, 1.0], true)
長方形の長辺が 2,小円の直径が 2/3,個数が 1 のとき,大円の直径は 1 である。
「術」の「(左側の小円の個数÷2 + 1)×小円径=大円径」は一般には成り立たない。
a = 4; b = 1.5; c = 2; n = 1; r1 = 0.666667; x1 = 2
小円の直径が 1,個数が 1,長方形の長辺が 4 のとき,大円の直径は 1.33333 である。
術による大円の直径 = 1.5
a = 4; b = 2.70711; c = 2.70711; n = 2; r1 = 1; x1 = 2.41421
小円の直径が 1,個数が 2,長方形の長辺が 4 のとき,大円の直径は 2 である。
術による大円の直径 = 2
a = 4; b = 4.10074; c = 2.83875; n = 3; r1 = 1.23801; x1 = 2.36272
小円の直径が 1,個数が 3,長方形の長辺が 4 のとき,大円の直径は 2.47602 である。
術による大円の直径 = 2.5
a = 4; b = 5.53944; c = 2.88985; n = 4; r1 = 1.39379; x1 = 2.29917
小円の直径が 1,個数が 4,長方形の長辺が 4 のとき,大円の直径は 2.78757 である。
術による大円の直径 = 3
a = 4; b = 7; c = 2.91667; n = 5; r1 = 1.5; x1 = 2.25
小円の直径が 1,個数が 5,長方形の長辺が 4 のとき,大円の直径は 3 である。
術による大円の直径 = 3.5
a = 20; b = 15.5568; c = 18.9657; n = 15; r1 = 5.17517; x1 = 14.4693
小円の直径が 1,個数が 15,長方形の長辺が 20 のとき,大円の直径は 10.3503 である。
術による大円の直径 = 8.5
a = 20
n = 15
r2 = 1/2
iniv = BigFloat[2, 1.5, 0.6, 1.2].*10
res = nls(H, ini=iniv)
function draw(more=false)
pyplot(size=(500, 500), showaxis=true, grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
(b, c, r1, x1) = res[1]
str = @sprintf("2r2=%g, n=%g, a=%g\n --> 2r1=%g", 2r2, n, a, 2r1)
@printf("a = %g; b = %g; c = %g; n = %g; r1 = %g; x1 = %g\n", a, b, c, n, r1, x1)
@printf("小円の直径が %g,個数が %g,長方形の長辺が %g のとき,大円の直径は %g である。\n", 2r2, n, a, 2r1)
@printf("術による大円の直径 = %g\n", (n/2 + 1)*2r2)
plot([0, a, a, 0, 0], [0, 0, b, b, 0], color=:blue, lw=0.5)
circle(x1, r1, r1)
circle(a - r2, b - r2, r2, :green)
for i = 1:n
circle(r2, b - (2i - 1)*r2, r2, :orange)
end
plot!([0, c, a], [0, b, 0], color=:magenta, lw=0.5)
if more
delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3 # size[2] * fontsize * 2
hline!([0], color=:gray80, lw=0.5)
vline!([0], color=:gray80, lw=0.5)
point(x1, 0.1r1, str, :black, :center, :bottom, delta=delta/2, mark=false)
point(x1, r1, "大円:r1,(x1,r1)", :red, :center, delta=-delta/2)
point(r2, b - (2n - 1)r2, "小円:r2,(r2,b-(2n-1)r2)", :black, :left, :bottom, delta=delta/2)
point(a - r2, b - r2,"小円:r2,(a-r2,b-r2)", :black, :right, delta=-delta/2)
end
end;


















