算額（その1365）

算額（その1365）

三十六 群馬県多野郡新町 稲荷神社 文政3年(1820)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：
#Julia, #SymPy, #算額, #和算

算額（その23），算額（その995）と算額（その396）を組み合わせた問題である。

図形と求めるものは，算額（その806）と同じである。
算額（その806）では与えられた条件を使って解を求めた。
今回の問題では，一般解を求める。

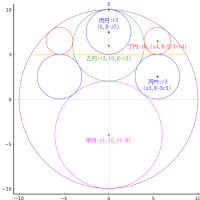
直角三角形の 3 辺を，「鈎」，「股」，「弦」
甲円の半径と中心座標を r1, (r1, r1)
乙円の半径と中心座標を r2, (x2, r2)
丁円の半径と中心座標を r3, (x3, r3)
とおき，以下の連立方程式を解く。
SymPy の性能上，一度に解を求めることができないので，まずは eq1, eq2, eq3, eq4 を解いて 「股」,r1, r2, x2 を求める。
得られた解を既知として，eq5, eq6 を解いて r3, x3 を求める。

include("julia-source.txt");

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     r1::positive, r2::positive, x2::positive,
     r3::positive, x3::positive;
eq1 = 鈎^2 + 股^2 - 弦^2
eq2 = 鈎 + 股 - 弦 - 2r1
eq3 = (x2 - r1) - 2sqrt(r1*r2)
eq4 = r2/(股 - x2) - r1/(股 - r1);
res1 = solve([eq1, eq2, eq3, eq4], (股, r1, r2, x2))[2]  # 2 of 2

   (sqrt(弦^2 - 鈎^2), -弦/2 + 鈎/2 + sqrt(弦^2 - 鈎^2)/2, (-弦*(4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*sqrt(弦^2 - 鈎^2) + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 3*鈎*sqrt(弦^2 - 鈎^2)) + 2*鈎*(-弦^2 + 弦*sqrt(弦^2 - 鈎^2) + 鈎^2) + sqrt(弦^2 - 鈎^2)*(4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*sqrt(弦^2 - 鈎^2) + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 3*鈎*sqrt(弦^2 - 鈎^2)))/(2*鈎^2), (4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*sqrt(弦^2 - 鈎^2) + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 3*鈎*sqrt(弦^2 - 鈎^2))/(2*鈎))

股 = sqrt(弦^2 - 鈎^2)
r1 = -弦/2 + 鈎/2 + sqrt(弦^2 - 鈎^2)/2
r2 = (-弦*(4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*sqrt(弦^2 - 鈎^2) + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 3*鈎*sqrt(弦^2 - 鈎^2)) + 2*鈎*(-弦^2 + 弦*sqrt(弦^2 - 鈎^2) + 鈎^2) + sqrt(弦^2 - 鈎^2)*(4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*sqrt(弦^2 - 鈎^2) + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 3*鈎*sqrt(弦^2 - 鈎^2)))/(2*鈎^2)
x2 = (4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*sqrt(弦^2 - 鈎^2) + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 3*鈎*sqrt(弦^2 - 鈎^2))/(2*鈎)
eq5 = (x3 - r1) - 2sqrt(r1*r3)
eq6 = (x2 - x3) - 2sqrt(r2*r3)
res2 = solve([eq5, eq6], (r3, x3))[1]

   ((2*sqrt(弦)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) + 2*弦^2 - 弦*鈎 - 2*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 鈎*sqrt(弦^2 - 鈎^2))^2/(2*(鈎*sqrt(-弦 + 鈎 + sqrt(弦^2 - 鈎^2)) + sqrt(-4*弦^(3/2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) + 4*sqrt(弦)*sqrt(弦^2 - 鈎^2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) - 8*弦^3 + 4*弦^2*鈎 + 8*弦^2*sqrt(弦^2 - 鈎^2) + 5*弦*鈎^2 - 4*弦*鈎*sqrt(弦^2 - 鈎^2) - 鈎^3 - 鈎^2*sqrt(弦^2 - 鈎^2)))^2), -弦/2 + 鈎/2 + sqrt((2*sqrt(弦)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) + 2*弦^2 - 弦*鈎 - 2*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 鈎*sqrt(弦^2 - 鈎^2))^2/(鈎*sqrt(-弦 + 鈎 + sqrt(弦^2 - 鈎^2)) + sqrt(-4*弦^(3/2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) + 4*sqrt(弦)*sqrt(弦^2 - 鈎^2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) - 8*弦^3 + 4*弦^2*鈎 + 8*弦^2*sqrt(弦^2 - 鈎^2) + 5*弦*鈎^2 - 4*弦*鈎*sqrt(弦^2 - 鈎^2) - 鈎^3 - 鈎^2*sqrt(弦^2 - 鈎^2)))^2)*sqrt(-弦 + 鈎 + sqrt(弦^2 - 鈎^2)) + sqrt(弦^2 - 鈎^2)/2)

丁円の半径は，「鈎」と「弦」を含む長い式になる。

-弦/2 + 鈎/2 + sqrt((2*sqrt(弦)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) + 2*弦^2 - 弦*鈎 - 2*弦*sqrt(弦^2 - 鈎^2) - 鈎^2 + 鈎*sqrt(弦^2 - 鈎^2))^2/(鈎*sqrt(-弦 + 鈎 + sqrt(弦^2 - 鈎^2)) + sqrt(-4*弦^(3/2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) + 4*sqrt(弦)*sqrt(弦^2 - 鈎^2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*sqrt(弦^2 - 鈎^2) - 弦*鈎^2 + 2*弦*鈎*sqrt(弦^2 - 鈎^2) + 鈎^3) - 8*弦^3 + 4*弦^2*鈎 + 8*弦^2*sqrt(弦^2 - 鈎^2) + 5*弦*鈎^2 - 4*弦*鈎*sqrt(弦^2 - 鈎^2) - 鈎^3 - 鈎^2*sqrt(弦^2 - 鈎^2)))^2)*sqrt(-弦 + 鈎 + sqrt(弦^2 - 鈎^2)) + sqrt(弦^2 - 鈎^2)/2

鈎 = 3 寸, 弦 = 6 寸を代入して，r3 = 0.20699488352959394 寸を得る。

---

鈎，弦として，与えられた数値そのままを用いて連立方程式を解けば，数値解が求まる。

using SymPy
@syms 鈎::positive, 股::positive, 弦::positive,
     r1::positive, r2::positive, x2::positive,
     r3::positive, x3::positive;
(鈎, 弦) = (3, 6)
eq1 = 鈎^2 + 股^2 - 弦^2
eq2 = 鈎 + 股 - 弦 - 2r1
eq3 = (x2 - r1) - 2sqrt(r1*r2)
eq4 = r2/(股 - x2) - r1/(股 - r1);
eq5 = (x3 - r1) - 2sqrt(r1*r3)
eq6 = (x2 - x3) - 2sqrt(r2*r3)
res1 = solve([eq1, eq2, eq3, eq4, eq5, eq6], (股, r1, r2, x2, r3, x3))[1]

   (3*sqrt(3), -3/2 + 3*sqrt(3)/2, -117/2 - 12*sqrt(14 - 8*sqrt(3)) + 6*sqrt(42 - 24*sqrt(3)) + 69*sqrt(3)/2, -15*sqrt(3)/2 + 6*sqrt(14 - 8*sqrt(3)) + 27/2, 3*(-3*sqrt(6) + 4*sqrt(7 - 4*sqrt(3)) + 5*sqrt(2))^2/(4*(sqrt(-39 - 8*sqrt(2)*sqrt(7 - 4*sqrt(3)) + 4*sqrt(6)*sqrt(7 - 4*sqrt(3)) + 23*sqrt(3)) + sqrt(-1 + sqrt(3)))^2), (3*sqrt(-2 + 2*sqrt(3))*(-3*sqrt(6) + 4*sqrt(7 - 4*sqrt(3)) + 5*sqrt(2))/2 + 3*(-1 + sqrt(3))*Abs(sqrt(-39 - 8*sqrt(2)*sqrt(7 - 4*sqrt(3)) + 4*sqrt(6)*sqrt(7 - 4*sqrt(3)) + 23*sqrt(3)) + sqrt(-1 + sqrt(3)))/2)/Abs(sqrt(-39 - 8*sqrt(2)*sqrt(7 - 4*sqrt(3)) + 4*sqrt(6)*sqrt(7 - 4*sqrt(3)) + 23*sqrt(3)) + sqrt(-1 + sqrt(3))))

Abs = abs
(3*sqrt(3), -3/2 + 3*sqrt(3)/2, -117/2 - 12*sqrt(14 - 8*sqrt(3)) + 6*sqrt(42 - 24*sqrt(3)) + 69*sqrt(3)/2, -15*sqrt(3)/2 + 6*sqrt(14 - 8*sqrt(3)) + 27/2, 3*(-3*sqrt(6) + 4*sqrt(7 - 4*sqrt(3)) + 5*sqrt(2))^2/(4*(sqrt(-39 - 8*sqrt(2)*sqrt(7 - 4*sqrt(3)) + 4*sqrt(6)*sqrt(7 - 4*sqrt(3)) + 23*sqrt(3)) + sqrt(-1 + sqrt(3)))^2), (3*sqrt(-2 + 2*sqrt(3))*(-3*sqrt(6) + 4*sqrt(7 - 4*sqrt(3)) + 5*sqrt(2))/2 + 3*(-1 + sqrt(3))*Abs(sqrt(-39 - 8*sqrt(2)*sqrt(7 - 4*sqrt(3)) + 4*sqrt(6)*sqrt(7 - 4*sqrt(3)) + 23*sqrt(3)) + sqrt(-1 + sqrt(3)))/2)/Abs(sqrt(-39 - 8*sqrt(2)*sqrt(7 - 4*sqrt(3)) + 4*sqrt(6)*sqrt(7 - 4*sqrt(3)) + 23*sqrt(3)) + sqrt(-1 + sqrt(3))))

   (5.196152422706632, 1.098076211353316, 0.6465370682525275, 2.7832432350115006, 0.2069948835295971, 2.0515879469406673)

以下は図を描くプログラムである。

function draw(鈎, 弦, more)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   股 = sqrt(弦^2 - 鈎^2)
   (r1, r2, x2) = (-弦/2 + 鈎/2 + 股/2, (-弦*(4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*股 + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*股 - 鈎^2 + 3*鈎*股) + 2*鈎*(-弦^2 + 弦*股 + 鈎^2) + 股*(4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*股 + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*股 - 鈎^2 + 3*鈎*股))/(2*鈎^2), (4*sqrt(弦)*sqrt(-(弦 - 鈎)*(-2*弦^2 + 2*弦*股 + 鈎^2)) + 4*弦^2 - 3*弦*鈎 - 4*弦*股 - 鈎^2 + 3*鈎*股)/(2*鈎))
   (r3, x3) = ((2*sqrt(弦)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*股 - 弦*鈎^2 + 2*弦*鈎*股 + 鈎^3) + 2*弦^2 - 弦*鈎 - 2*弦*股 - 鈎^2 + 鈎*股)^2/(2*(鈎*sqrt(-弦 + 鈎 + 股) + sqrt(-4*弦^(3/2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*股 - 弦*鈎^2 + 2*弦*鈎*股 + 鈎^3) + 4*sqrt(弦)*股*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*股 - 弦*鈎^2 + 2*弦*鈎*股 + 鈎^3) - 8*弦^3 + 4*弦^2*鈎 + 8*弦^2*股 + 5*弦*鈎^2 - 4*弦*鈎*股 - 鈎^3 - 鈎^2*股))^2), -弦/2 + 鈎/2 + sqrt((2*sqrt(弦)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*股 - 弦*鈎^2 + 2*弦*鈎*股 + 鈎^3) + 2*弦^2 - 弦*鈎 - 2*弦*股 - 鈎^2 + 鈎*股)^2/(鈎*sqrt(-弦 + 鈎 + 股) + sqrt(-4*弦^(3/2)*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*股 - 弦*鈎^2 + 2*弦*鈎*股 + 鈎^3) + 4*sqrt(弦)*股*sqrt(2*弦^3 - 2*弦^2*鈎 - 2*弦^2*股 - 弦*鈎^2 + 2*弦*鈎*股 + 鈎^3) - 8*弦^3 + 4*弦^2*鈎 + 8*弦^2*股 + 5*弦*鈎^2 - 4*弦*鈎*股 - 鈎^3 - 鈎^2*股))^2)*sqrt(-弦 + 鈎 + 股) + 股/2)
   @printf("鈎 が %g，弦 が %g のとき，丁円の直径は %g である。\n", 鈎, 弦, 2r3)
   @printf("鈎 = %g;  弦 = %g;  股 = %g;  r1 = %g;  r2 = %g;  x2 = %g;  r3 = %g;  x3 = %g\n", 鈎, 弦, 股, r1, r2, x2, r3, x3)
   println("r3 = $r3")
   plot([0, 股, 0, 0], [0, 0, 鈎, 0], color=:magenta, lw=0.5)
   circle(r1, r1, r1)
   circle(x2, r2, r2, :blue)
   circle(x3, r3, r3, :green)
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, r1, "甲円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(x2, r2, "乙円:r2,(x2,r2)", :blue, :center, delta=-delta/2)
       point(x3, r3, "丁円:r3,(x3,r3)", :green, :center, delta=-5delta)
       point(0, 鈎, "鈎 ", :magenta, :right, :vcenter)
       point(股, 0, " 股", :magenta, :center, delta=-delta)
       dimension_line(delta, 鈎 + 2delta, 股 + delta, 2delta, "弦", :gray50, delta=2delta, deltax=2delta)
       plot!(xlims=(-8delta, 股 + 3delta), ylims=(-6delta, 鈎 + 4delta))
   end  
end;

draw(3,6, true))