算額（その1366）

算額（その1366）

三十六 群馬県多野郡新町 稲荷神社 文政3年(1820)
群馬県和算研究会:群馬の算額，上武印刷株式会社，高崎市，1987年3月31日.
キーワード：円8個，等脚台形
#Julia, #SymPy, #算額, #和算

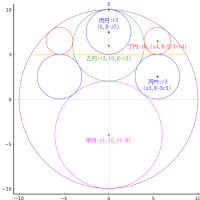
等脚台形の中に，大円 5 個，小円 3 個を容れる。台形の上底が与えられたとき，小円の直径はいかほどか。

注：算額（その1364）の設問の不備を修正し，枝葉を取り除いたものである。

等脚台形の下底，上底，高さを 2a, 2b, h
大円の半径と中心座標を r1, (2r1, r1), (r1, h - r1)
小円の半径と中心座標を r2, (0, 2r1 + r2)
甲円の半径と中心座標を r3, (x3, r3)
乙円の半径と中心座標を r4, (0, h - r4)
とおき，以下の連立方程式を解く。
方程式は算額（その1364）と同じで，与える条件と求めるパラメータが違うだけである。
甲円と乙円のパラメータも求めておく（図には描かない）。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, h::positive,
     r1::positive, r2::positive,
     r3::positive, x3::positive, r4::positive;
eq1 = r1^2 + (h - 2r1)^2 - 4r1^2
eq2 = r1/(a - 2r1) - 1/√Sym(3)
eq3 = r1/(b - r1) - √Sym(3);
# res1 = solve([eq1, eq2, eq3], (r1, a, h));

eq4 = r1^2 + (h - r1 - (2r1 + r2))^2 - (r1 + r2)^2
eq5 = r1^2 + (r1 - r4)^2 - (r1 + r4)^2;
# res = solve([eq1, eq2, eq3, eq4, eq5], (r1, r2, r4, a, h))

eq6 = r3/(a - x3) - 1/√Sym(3)
eq7 = x3 - 2r1 - 2sqrt(r1*r3)
res = solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7],
   (r1, r2, r3, x3, r4, a, h))[1]  # 2 of 2

   (b*(3 - sqrt(3))/2, -989*b*sqrt(151316*sqrt(3) + 262087) - 3*b/2 + sqrt(3)*b/2 + 571*sqrt(3)*b*sqrt(151316*sqrt(3) + 262087), b*(3 - sqrt(3))/6, 2*b, b*(3 - sqrt(3))/8, b*(sqrt(3) + 3)/2, b*(-2967*sqrt(151316*sqrt(3) + 262087) - 2*sqrt(3) + 6 + 1713*sqrt(453948*sqrt(3) + 786261))/2)

パラメータによっては二重根号を外して簡約化できる。

r1
res[1] |> println

   b*(3 - sqrt(3))/2

r2
res[2] |> sympy.sqrtdenest |> simplify |> println

   b*(-5 + 3*sqrt(3))/2

r3
res[3] |> sympy.sqrtdenest |> simplify |> println

   b*(3 - sqrt(3))/6

x3
res[4] |> sympy.sqrtdenest |> simplify |> println

   2*b

r4
res[5] |> println

   b*(3 - sqrt(3))/8

a
res[6] |> println

   b*(sqrt(3) + 3)/2

h
res[7] |> sympy.sqrtdenest |> simplify |> println

   b*(sqrt(3) + 3)/2

小円の半径は b*(3 - sqrt(3))/6 なので，上底が 14 寸のとき小円の直径は 14*(3 - sqrt(3))/6 = 2.95854811567262 寸である。
このとき，下底は 32*(3 - sqrt(3))/3 = 13.524791385931977 である。

全てのパラメータは以下のとおりである。

   a = 16;  r1 = 4.28719;  r2 = 0.66323;  r3 = 1.42906;  x3 = 13.5248;  r4 = 1.0718;  b = 6.7624;  h = 16

---

なお，小円の直径を知るだけならば，以下のような手順で小円の直径を（紙と鉛筆だけで）求めることができる。

上底 2b と大円の半径 r1 の関係式は以下であり，大円の半径は r1 = b*(3 - √3)/2 である。

@syms b, r1
eq01 = (1 + 1/√Sym(3))r1 - b
eq01 |> println

   -b + r1*(sqrt(3)/3 + 1)

r1 = solve(eq01, r1)[1] |> simplify
r1 |> println

   b*(3 - sqrt(3))/2

一辺の長さが 2r1 の正三角形の頂点を中心とする3個の大円が作る中央の隙間にピッタリハマる円の半径は以下のようになる（図中の灰色で描いた小さな直角三角形を参照）。

r1*2/√Sym(3) - r1 |> simplify |> println

    b*(-5 + 3*sqrt(3))/2

上底が 14 寸のとき，小円の直径は 1.3730669589464242 寸である。

b = 14/2
2*b*(-5 + 3*sqrt(3))/2

   1.3730669589464242

function draw(b, more)
   pyplot(size=(800, 800), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3, x3, r4, a, h) = (b*(3 - sqrt(3))/2, -989*b*sqrt(151316*sqrt(3) + 262087) - 3*b/2 + sqrt(3)*b/2 + 571*sqrt(3)*b*sqrt(151316*sqrt(3) + 262087), b*(3 - sqrt(3))/6, 2*b, b*(3 - sqrt(3))/8, b*(sqrt(3) + 3)/2, b*(-2967*sqrt(151316*sqrt(3) + 262087) - 2*sqrt(3) + 6 + 1713*sqrt(453948*sqrt(3) + 786261))/2)
   r1 = b*(3 - √3)/2
   r2 = b*(3√3 - 5)/2
   r3 = b*(3 - √3)/6
   x3 = 2b
   r4 = b*(3 - √3)/8
   a = b*(√3 + 3)/2
   h = b*(√3 + 3)/2
   @printf("上底が %g のとき，小円の直径は %g である（下底は %g）。\n", 2b, 2r2, 2a)
   @printf("b = %g;  r1 = %g;  r2 = %g;  r3 = %g;  x3 = %g;  r4 = %g;  a = %g;  h = %g\n", b, r1, r2, r3, x3, r4, a, h)
   plot([a, b, -b, -a, a], [0, h, h, 0, 0], color=:green, lw=0.5)
   circle(0, r1, r1)
   circle2(2r1, r1, r1)
   circle2(r1, h - r1, r1)

   circle(0, 2r1 + r2, r2, :blue)
   circle2(r1, h - 2r1 - r2, r2, :blue)

   #=
   circle(0, h - r4, r4, :green)
   circle2(r1, r4, r4, :green)

   circle2(x3, r3, r3, :orange)
   l = h - (2r1 + r2) - r4
   circle2(r1 + l*cosd(30), h - (2r1 + r2) + l*sind(30), r4, :green)
   =#
   if more
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(2r1, r1, "大円:r1,(2r1,r1)", :red, :center, delta=-delta)
       point(0, r1, "大円:r1,(0,r1)", :red, :center, delta=-delta)
       point(r1, (1 + √3)r1, "大円:r1,(r1,(1+√3)r1)", :red, :center, delta=-delta)
       point(0, 2r1 + r2, "小円:r2,(0,2r1+r2)", :blue, :left, :vcenter, deltax=4delta)
       #=
       point(0, h - r4, "乙円:(0,h-r4)", :green, :left, :vcenter, deltax=7delta)
       point(x3, r3, "甲円:(x3,r3)", :orange, :right, :vcenter, deltax=-9delta)
       =#
       point(b, h, "(b,h)", :brown, :right, :bottom, delta=delta/2)
       point(a, 0, "a", :brown, :left, :bottom, delta=delta/2)
       plot!([r1, 2r1, r1, r1], [r1, r1, h - 2r1 - r2, r1], color=:gray70, lw=0.5)
   end  
end;

draw(14/2, true)